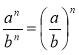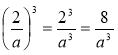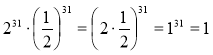Властивості степеня (продовження). Степінь добутку й відношення

Тема. Властивості степеня (продовження). Степінь добутку й відношення

Мета: домогтися свідомого розуміння властивості степеня добутку й відношення; виробити вміння застосовувати ці властивості для перетво­рень виразів і обчислення значень числових виразів.

Тип уроку: засвоєння знань, умінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

 Як і на попередніх двох уроках, перевірку домашнього завдання можна виконати у вигляді самостійної роботи (бліцконтроль), зав­дання якої є квінтесенцією завдань домашнього завдання.

Бліцтест

1. Яка з рівностей є правильною:

1) (y⁴)³ = y¹²; 2) (m⁵)⁴ = m²⁵; 3) ((a⁷)³)² = a²¹; 4) a³² : (a⁹)³ = a⁵?

2. Виконайте дії:
   1) m⁵m⁴; 2) (a⁶)³ · (a²)⁴; 3) (a⁵)³ · (a⁴)⁷ : a¹²; 4) (11³)⁴ : (11⁵)².
3. Подайте у вигляді степеня: .

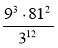Після виконання вправ звіряємо відповіді з відповідями у виконаному домашньому завданні.

II. Робота з випереджальним домашнім завданням

Учні працюють з алгоритмом доведення (див. додатки).

Варіант 1: довести, що (2 · 3)⁵ = 2⁵ · 3⁵.

Варіант 2: довести, що .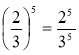

(Відповідні записи учні виконують на окремих аркушах.) Після виконання завдань два учні презентують біля дошки свої дове­дення (за пунктами плану); решта учнів працює зі своїми роботами — проводять (у разі необхідності) корекцію. Бланки відповідей мають такий вигляд:

III. Засвоєння знань

 Після проведеної роботи із випереджальним домашнім завданням все, що залишається для усвідомлення загальних властивостей, — це пройти ті ж самі етапи доведення, але для загальних випадків:

(аb)^п = а^п b^п  та .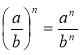

Під час формулювання властивостей і запису їх у вигляді тотожностей необхідно наголосити на тому, що це тотожності, тобто вираз у правій частині можна замінити, перетворюючи вирази, на вираз, що міститься в лівій частині, і навпаки.

Останній момент, на якому слід акцентувати,— це місце вказаних вла­стивостей серед доведених раніше.

Записи в зошитах учнів можуть мати такий вигляд:

IV. Засвоєння вмінь та навичок

 Система завдань, запропонованих на урок, складається із вправ:

1. на безпосереднє застосування названих властивостей (степінь добут­ку та степінь відношення);
2. на практичне застосування теоретичних відомостей;
3. на засвоєння вмінь працювати з буквеними показниками степеня;
4. на подання виразів у вигляді степеня (добутку або відношення);
5. на використання властивостей степеня для виконання обчислень.

Виконання усних вправ

1. Яке число треба піднести до другого степеня, щоб дістати:

9; 81; 0; 16; ; 0,0036?

Яке число треба піднести до третього степеня, щоб дістати:

8; -27; -; -0,064; 0,125?

2. Виконайте піднесення до степеня: (ab)³; 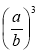; (3х²)³; .
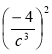3. Подайте у вигляді степеня: 2² · 3²; 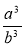; x⁶ · y⁶; 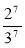; (-2,5)³ · 4³.
4. Яке число треба підставити замість *, щоб рівність стала правильною:

5⁷ · 3^* = 15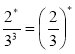^*; ; а^2пb^* = (*b)ⁿ?

5. Подайте у вигляді добутку: а⁵; 12⁷; (ab)⁵; (12а)⁷.

Виконання письмових вправ

1. Подайте степінь у вигляді добутку:

1) (аb)⁵; 2) (тпр)⁹; 3) (3х)⁴; 4) (-2dc)³; 5) (-0,2аb)⁴; 6) .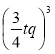

Звертаємо увагу на те, що під час перетворення добутку степенів у сте­пінь добутку, показники множників повинні бути однакові.

2. Подайте добуток у вигляді степеня:

1) a³ · y³; 2) -27b⁹; 3) 16a²b²; 4) 32a⁵b⁵; 5) - a³b³;  6) 1024m¹⁰n¹⁰.

3. Обчисліть значення виразу:

1) (0,25)⁶ · 4⁶;  2) 3⁴ · 2⁴;  3) · 6⁵;   4) 0,5⁵ · 4⁵;

5) 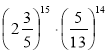;   6) (0,125)¹⁰ · 8¹².

4. Як зміниться площа квадрата, якщо його сторону збільшити у 2 рази; у 3
   рази; у 10 разів; у п разів?

5*. Об'єм кулі обчислюється за формулою V = πr³, де r — радіус кулі. Як зміниться об'єм кулі, якщо радіус кулі збільшити у 2; у 4; у т разів?

6*. Подайте у вигляді добутку:

1) (ab)²ⁿ;  2) (а²b)ⁿ; 3) (а²b³)ⁿ⁺¹; 4) (аⁿ⁺¹bⁿ)².

7*. Логічна вправа. Знайдіть пропущене число.

V. Підсумок уроку

Чи знаєш ти властивості степеня?

Розстав знаки дій, числа, дужки, щоб з поданих виразів зліва утвори­лися вирази, що записані праворуч:

а⁷  а⁴, а⁷  а¹⁰, а⁷  а²¹, аb  а⁷b²¹, .

VI. Домашнє завдання

№ 1. Подайте у вигляді добутку степені:

1) (аb)⁸; 2) (xyz)¹⁰; 3) (2х)⁵; 4) (-3аb)⁴; 5) (-0,1mn)⁶; 6) .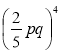

№ 2. Обчисліть значення виразу:

1) 0,5⁸ · 2⁸;   2) 2⁵ · 5⁵;  3) 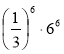;   4) 0,125⁹ · 8⁹;

5) ;   6) (0,25)²⁰ : 4²².

№ 3. Випереджальне домашнє завдання. Використовуючи текст під­ручника (тема «Властивості степеня»), з'ясуйте й запишіть:

1. Які арифметичні дії і з якими степенями ви вмієте виконувати? Проілюструйте відповідними рівностями.
2. Складіть алгоритм виконання виписаних вами дій.