Заняття №1-2 на тему: «Подільність чисел. Властивості й ознаки подільності чисел»

Заняття №1-2 на тему: «Подільність чисел. Властивості й ознаки подільності чисел»  до програми факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики».

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв’язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 1. Подільність і прості числа

Заняття № 1-2

Подільність чисел. Властивості й ознаки подільності чисел

Як встановити, чи поділиться одне число на інше без остачі? Для цього потрібно знати основні поняття і теореми, пов’язані з подільністю.

Ділення числа а на в можна виразити рівністю:  , де і – цілі числа, – частка, – остача, .

При діленні на  можуть бути остачі:

Якщо , це означає, що ділиться на без остачі: , .

Подільність – це відношення, яке можна записувати парами, таблицями, стрілками тощо.

Подільність чисел має властивості:

1. Рефлективність ;
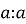
2. Транзитивність   то ;
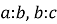
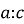
3. Антисиметричність  , то .

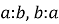
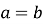
Основні теореми, пов’язані з подільністю:

1.               (теорема про подільність суми) Якщо кожний доданок ділиться на натуральне число , то і сума ділиться на це число. Наприклад, 114+348+908 ділиться на 2? Так як .
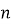
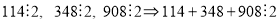2.               (теорема про подільність різниці) Якщо числа діляться на число і , то їх різниця .
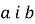
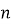
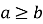
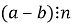
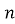
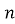
3.               (теорема про подільність добутку) Якщо один з множників добутку ділиться на число, то і весь добуток ділиться на число. Наприклад, ?. Так як .
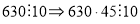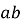
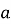
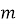
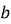
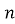
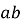
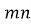
4.               Якщо в добутку чисел 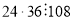множник ділиться на число , а число на число, то добуток ділиться на добуток . Наприклад, ?. Число 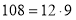, тоді 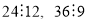, значить .
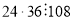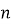
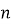
5.               Якщо в сумі один доданок не ділиться на число 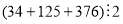, а решта доданків ділиться , то вся сума не ділиться на число . Наприклад, ? Так як число 125 не ділиться на 2, значить вся сума не ділиться на 2.

Розв'язування задач і вправ.

•             Сума цифр трицифрового числа, всі цифри якого різні, ділиться на 7. Крім того, саме це число ділиться на 7. Знайдіть всі ці числа.

Розв'язання.

Нехай дане число. За умовою число і .

Маємо .

Звідси число але також ділиться на 7, проте і ділиться на 7. Перебором цифр, але так, щоб виконувалася умова визначаємо шукані  числа:

Отже, шукані числа 329, 392, 518, 581.

Відповідь:  329, 392, 518, 581.

•             Знайдіть серед чисел виду три числа, кратні 5.

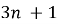
Розв’язання.

Для того, щоб число виду ділилося на 5, необхідно, щоб остання цифра в записі цього числа була 0 або 5. Нехай ці числа закінчуються на 0, тоді числа виду повинні закінчуватися на 9 і ділитися на 3.

Розглянемо деякі з них, що задовольняють першу вимогу:

9,19,29,39,40,59,69, … .

Виберемо з них ті, що задовольняють і другу вимогу: 9,39,69, … .

Отже, серед чисел виду на 5 діляться числа: 9+1=10, 39+1=40, 69+1=70.

Відповідь. 10; 40; 70.

•             До числа 10 справа і зліва приписати по одній цифрі так, щоб дістати число кратне 72.

Розв'язання.

, тому знайдене число має ділитися на 8 і 9. Тоді воно парне і сума цифр ділиться на 9. Цим умовам задовольняють числа: 6102, 4104, 2106, 9108. З цих чисел на 8 ділиться лише 4104.

Відповідь. 4104

•             Чи існує таке двоцифрове число, яке у два рази менше від двоцифрового числа, кожна цифра якого більша на 2 одиниці від цифр даного числа?

Розв'язання.

Нехай   цифра десятків, цифра одиниць шуканого числа. Маємо рівність , тобто . Оскільки і – цифри, то маємо

Завдання для самостійного розв’язування

1. Чи ділиться добуток на 2; на 5; на 10?
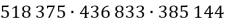
2. Чи ділиться сума 2126 + 3578 + 731 на 2; на 5; на 10?
3. Використовуючи  цифри 0, 1, 4, 5, 7 запишіть шість чотирицифрових чисел, кожне з яких не містить однакових цифр і два з яких діляться на 2, два – на 5, два – на 10.
4. Використовуючи цифри 0, 2, 6, 9, запишіть три чотирицифрових числа, кожне з яких не містить однакових цифр і перше з яких ділиться на 2, друге – на 5, третє – на 10.
5. Використовуючи кожну з цифр один раз, запишіть найменше натуральне число, яке ділиться на 2; на 5; на 10.
6. Використовуючи кожну з цифр один раз, запишіть найбільше натуральне число, яке:

1. ділиться на 2, але не ділиться на 10;
2.  ділиться на 5, але не ділиться на 2.

7. Запишіть найменше чотирицифрове число, яке ділиться на 10 і сума цифр якого дорівнює 10.
8. Запишіть найбільше чотирицифрове число, яке ділиться на 10 і сума цифр якого дорівнює 11.
9. Випишіть усі натуральні числа, розміщені між числами 179 і 205, які діляться на 2, але не діляться на 5.
10. Дано ряд чисел 1, 2, 3,…, 99, 100. Скільки серед них є парних і скільки непарних? Скільки чисел ділиться на 5 і скільки на 10?

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.