Заняття №3-4 на тему: «Найбільший спільний дільник двох чисел. Алгоритм Евкліда»

Заняття №3-4 на тему: «Найбільший спільний дільник двох чисел. Алгоритм Евкліда»  до програми факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики».

 

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв’язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

 

Тема 1. Подільність і прості числа

Заняття 3 – 4

Найбільший спільний дільник двох чисел. Алгоритм Евкліда

Розглянемо числа12 і 8. Їх дільники і. У чисел 12 і 8 існують спільні дільники 1, 2, 4. Серед них є найбільше число 4, його називають найбільшим спільним дільником НСД.

Спільним дільником чисел називається кожне натуральне число, яке являється дільником кожного з даних чисел. НСД чисел називається найбільше число з усіх спільних дільників даного числа.

Властивості НСД:

1.          НСД завжди існує і являється єдиним;
2.          НСД не перевищує меншого з даних чисел;
3.          НСД ділиться на кожний дільник цих чисел.

Знаходження НСД чисел способом розкладу на прості множники.

Запис числа в виді добутку простих чисел називається розкладом цього числа на прості множники. Наприклад, число 720=, або і .

В розклад на прості множники НСД мають ввійти всі спільні прості множники, які містяться в розкладі даних чисел, причому кожен з них потрібно взяти з найменшим степенем, з яким вони входять в обидва розклади.

Алгоритм знаходження НСД.

1. представляємо число в канонічному виді;
2. утворюємо добуток спільних для чисел простих множників, причому кожний з них обираємо з найменшим степенем, з яким вони входять до розкладу. Обчислюємо значення добутку – це НСД даних чисел.

Якщо НСД двох чисел одиниця, то ці числа – взаємно прості.

Евклід - давньогрецький математик, що жив у ІІІ ст. до н.е. В своїй  праці «Начала» він описав спосіб знаходження НСД натуральних чисел.

Щоб знайти НСД двох чисел, використовуючи алгоритм Евкліда, необхідно:

1) поділити більше з них на менше, дістанемо неповну частку і остачу;

2) ділимо менше з даних чисел на здобуту (першу остачу) і дістанемо другу неповну частку і остачу;

3)  ділимо першу остачу на другу і т.д., при цьому остача зменшується;

4). ділимо до тих пір, поки остача не стане рівною 0.

Остання відмінна від нуля остача і є шуканий НСД двох чисел.

Вправа 1. Знайти НСД(200; 375)

				375			200
				200			1
		200		175
		175	1
175		25
175	7
0

Отже, НСД(200;375)=25.

Вправа 2. Скоротити дроби:

а) ;   б) .

Розв'язування задач і вправ.

•             Яку найбільшу кількість однакових букетів можна скласти із 6 волошок і 9 ромашок?

Розв'язання.

Треба знайти найбільше число, на яке ділиться 6 і 9, тобто найбільший спільний дільник цих чисел.

НСД (6,9)=3. Отже, можна скласти 3 букета.

Відповідь. 3 букета.

•             Яку найбільшу кількість однакових букетів можна скласти із 24 волошок і 32 ромашок, використавши всі квіти?

Розв'язання.

3 даних квітів можна, наприклад, скласти 2 букети, у кожному з яких буде 12 волошок і 16 ромашок. Не можна скласти три букети, бо 32 ромашки не можна розділити на 3 однакові частини. Можна скласти чотири однакові букети, бо і 2 волошки, і 32 ромашки можна розділити на 4 однакові частини. Очевидно, що для розв'язання задач потрібно знайти  найбільше число, на яке можна розділити 24 волошки і 32 ромашки, тобто знайти найбільши спільний дільник чисел 24 і 32.

Оскільки НСД (24; 32) = 8, то найбільше можна скласти 8 однакових букетів. Кожний такий букет складатиметься із 24: 8 = 3 волошок і 32: 8 = 4 ромашок.

Відповідь. 8.

•             Скільки існує тризначних чисел, які при діленні на 8 дають в остачі 3?

Розв'язання.

Всього є 900 тризначних чисел. Розіб’ємо їх на групи по 8 чисел в кожній:

100,101, 102,…, 107;

108, 109, 110, …, 115,…

В кожній з цих груп є лише одне число, а саме останнє – 107, 115, …, яке при діленні на 8 дає в остачі 3. Всього таких груп є тобто 112 повних груп і одна неповна, в якій такого числа немає. Отже, всього таких чисел є 112.

Відповідь:112.

•                 Доведіть, що число 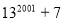кратне 10.

Розв'язання.

Спочатку довести, що якщо 13 підносити до степеня, який при поділі на 4 дає остачу 1, то число закінчується 3, а отже, додавши 7, маємо останню цифру 0, тому число ділиться на 10.

•             Доведіть, що добуток трьох послідовних натуральних чисел ділиться на 6.

Розв'язання.

Серед трьох послідовних натуральних чисел п, п+1, п+2  є хоча б одне парне число й одне число, що ділиться на 3. Оскільки числа  2 та  3 взаємно-прості, то добуток п(п+1)(п+2) ділиться на .

Зауваження. Добуток  трьох послідовних чисел п(п+1)(п+2) ділиться на

Завдання для самостійного розв’язування

1.               Яку найбільшу кількість однакових подарунків можна скласти із 48 цукерок і 36  яблук, якщо використати всі цукерки й усі яблука?
2.               Прямокутний аркуш паперу завдовжки 56 см і завширшки 48 см потрібно розрізати без відходів на найменшу кількість рівних квадратів. Скільки квадратів одержимо?
3.               Дерев'яний брусок завдовжки 48 см, завширшки 30 см і заввишки 24 см потрібно розрізати без відходів на найменшу кількість рівних кубів. Скільки кубів одержимо?
4.               Яку найбільшу кількість однакових подарунків можна скласти з 90 мандаринів, 405 цукерок і 135 пряників, якщо потрібно використати всі мандарини, цукерки і пряники?
5.               Між усіма учнями класу розділили порівну 58 зошитів у лінійку і 87 зошитів у клітинку. Скільки учнів у класі? Скільки зошитів у лінійку і скільки у клітинку отримав кожен учень?
6.               У кімнаті завдовжки 625 см і завширшки 475 см вирішили викласти долівку однаковими декоративними плитками квадратної форми, не розрізуючи їх. Який найбільший можливий розмір такої плитки? Скільки плиток найбільшого розміру потрібно, щоб викласти ними долівку?

 

 

 

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.