Заняття №5-6 на тему: «Прості числа. Нескінченність множини простих чисел»

Заняття №5-6 на тему: «Прості числа. Нескінченність множини простих чисел»  до програми факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики».

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв’язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 1. Подільність і прості числа

Заняття 5-6

Прості числа. Нескінченність множини простих чисел

Історія математики знає імена вчених, які чимало працювали над складанням таблиці простих чисел. Перші спроби робились ще в Стародавній Греції.

Те, що найбільшого простого числа не існує, ще в 4ст. до н.е. довів давньогрецький математик Евклід. Він сформулював це так: «Простих чисел існує більше від будь-якої запропонованої кількості. Поняття простого і складеного числа виникло ще в 5ст. до н.е. у піфагорійців. Прості числа вони ще називали «першими», складені – «другими». Складені числа, які є квадратами натуральних, називали «квадратними», інші складені числа – «прямокутними». Ці назви пов’язані з тим, що піфагорійці зображали числа за допомогою точок, які утворювали певну фігуру.

Для знаходження простих чисел давньогрецький учений Ератосфен запропонував певний спосіб. Він виписував усі числа від 1 до якогось числа а. Викреслював число 1, яке не є простим. Підкреслював число  2 і викреслював усі числа, які діляться на 2, тобто числа 4, 6, 8,… Наступне закреслюване число 3 є простим. Ератосфен підкреслював це число і викреслював усі числа, які діляться на 3. Підкреслював наступне не викреслене число, яке є простим, і т.д. У такий спосіб серед чисел, що не перевищують а, можна «висіяти» всі прості числа.

Якщо «висіяти» всі прості числа, що не перевищують 30, то одержимо: 2,3,5,7,11,13,17,19,23,29 - перші 10 простих чисел.

Метод Ератосфен «висіювання» простих чисел називають ще «решетом Ератосфен». Це пов’язано з тим, що давні греки писали на папірусах або табличках, покритих воском, і числа не викреслювали, а виколювали голкою, після чого папірус або табличка нагадували решето.

Число 1 і прості числа не можна подати у вигляді добутку простих чисел. А от кожне складене число можна подати у вигляді добутку кількох простих множників.

Основна теорема арифметики:

Кожне відмінне від одиниці натуральне число можна розкласти на прості множники єдиним способом.

Теорема ЕВКЛІДА.

Множина простих чисел нескінченна.

Розв'язування задач і вправ.

•             Чи може сума трьох послідовних натуральних чисел бути простим числом? Доведіть.

Розв'язання.

Розглянемо суму  трьох послідовних натуральних чисел (п-1)+п+(п+1)=3п. Вираз 3п ділиться на 3, тому не може  бути простим числом.

•             Просте чи складене число ?

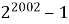Розв'язання.

. Кожний з множників відмінний від 1 і самого числа. Отже, число складене.

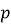
•             Якщо 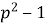– просте число, більше ніж 3, то ділиться на 24. Доведіть.

Розв'язання.

Розкладемо числа 24  та на множники:

24=3∙8,

.

Розглянемо добуток послідовних цілих чисел. Одне з них обов’язково ділиться на 3. За умовою - просте, тому не ділиться на 3. Це означає, що або ділиться на 3, або ділиться на 3. В обох випадках ділиться на 3. Оскільки і – просте число, то воно непарне. А і – послідовні парні числа. Одне з них обов’язково ділиться на 2, а інше – на 4, а їх добуток – на 8. Тоді  ділиться на 3∙8=24.

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.