Заняття № 7-8 на тему: «Конгруенції та їх властивості. Класи чисел та мала теорема Ферма»

Заняття № 7-8 на тему: «Конгруенції та їх властивості. Класи чисел та мала теорема Ферма»  до програми факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики».

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв’язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 1. Подільність і прості числа

Заняття 7 – 8

Конгруенції та їх властивості. Класи чисел та мала теорема Ферма

Означення1. Числа і b  називаються конгруентними за модулем , де - натуральне число, якщо їх різниця ділиться на . Записується , якщо .

Означення 2. Цілі числа називаються конгруентними за модулем, якщо при діленні на мають однакові остачі. Записується , де і - цілі числа, - остача від ділення, .

Якщо числa і   при діленні на мають однакові остачі, то їх різниця ділиться на і навпаки.

Властивості конгруенції:

1. Рефлективність: (ціле число конгруентне само собі).
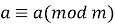
2. Симетричність: , то .
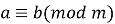
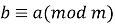
3. Транзитивність: 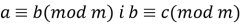то .
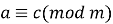
4. Конгруенції за одним модулем можна додавати:

Наслідки:

1. члени конгруенції можна переносити з однієї частини в іншу, змінивши знак на протилежний: .
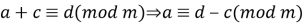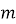
2. до будь-якої частини конгруенції можна додати одне  і те ж число, кратне модулю 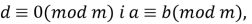: то .
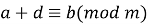
3. конгруенції за одним і тим же модулем можна почленно  перемножити:

і , то .

4. oбидві частини конгруенції можна підносити до одного і того ж степеня з натуральним показником: 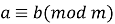, то .
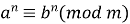5. oбидві частини конгруенції можна  помножити на те саме ціле число: .
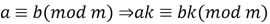6. oбидві частини конгруенції можна  поділити на їх спільний дільник, якщо він взаємно-простий з модулем (: .
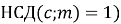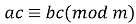
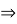
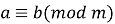7. oбидві  частини конгруенції і модуль можна  поділити на їх спільний дільник.

Розв'язування задач і вправ.

•             Назвати натуральні числа, менші 100, конгруентні з числом:

а) за модулем 20;            б) за модулем 25.

Розв'язання.

а) ,

бо ,

бо ,

бо ,

бо .

Відповідь: 24, 44, 64, 84.

•             Знайти модулі, за якими числа 43  і  16  - конгруентні.

Розв'язання.

43-16=27, а 27 ділиться на 3, 9, 27.

Відповідь: 3, 9, 27.

Класи чисел і мала теорема Ферма.

При розв’язуванні більш складних задач на подільність чисел на, треба розбити множину цілих чисел на класів в залежності від остач, які одержуємо при діленні на .

Наприклад, т=4.Які можуть бути остачі при діленні на 4? r=0,1,2,3. Тому всі числа розіб’ємо на чотири класи:

Нульовий – остача 0;  перший – остача 3; другий – остача 2; третій – остача 1.

З цього випливає, що:

1) кожен з утворених класів має безліч чисел;

2) усі числа будь-якого одного класу конгруентні між собою за даним модулем;

3) будь-які числа з різних класів не конгруентні.

Мала теорема Ферма:

Яке б не було число і просте , то або .

Наприклад, (а⁵-а):5,  (а²⁰-а):20.

Користуючись малою теоремою Ферма , можна доводити подільність на складені числа.

Розв'язування задач і вправ.

•             Довести, що (а⁵-а):30,  а-  ціле число.

Доведення.

1. За малою теоремою Ферма (а⁵-а):5;
2. Потрібно довести, що ця різниця ділиться і на 2, і на 3. Оскільки

(а⁵-а)=а(а⁴-1)=а(а²-1)(а²+1)=а(а-1)(а+1)(а²+1), маємо три послідовних цілих числа, тому добуток їх ділиться на 2 і ділиться на 3.

3. Числа 2,3,5 попарно взаємно-прості, отже, (а⁵-а):30.

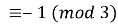
•             Знайдіть остачу від ділення 2012²⁰¹³ на 3. Розглянемо конгруенцію 2012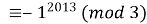, тоді 2012²⁰¹³, 2012²⁰¹³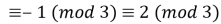. Отже, остача від ділення дорівнює 2.
•             Остача від ділення трицифрового числа n= 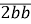на деяке одноцифрове число дорівнює 8, знайдіть число n.

Оскільки остача від ділення 8, тоді розглянемо конгруенцію за модулем 9: n, тоді

2·100+10b+b,

200+11b,

11b,

11b,

11b,

11b,

b.

Отже, шукане число b=,  n=233.

•             Доведіть, що 15ⁿ + 2³ⁿ – 30  кратне 7.

Оскільки 15, 2³,тоді 15ⁿ + 2³ⁿ,

15ⁿ + 2³ⁿ,  15ⁿ + 2³ⁿ.

Завдання для самостійного розв’язування.

1. Відновіть запис:

34,  4,  -1,

, -2, *.

2. Знайдіть остачу від ділення 29²⁰¹³ на 4;      5²⁰¹⁴  на 3.
3. Остача від ділення трицифрового числа n= 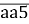на деяке одноцифрове число дорівнює 8, знайдіть число n.
4. Доведіть, що 6²ⁿ + 3ⁿ⁺² +3ⁿ кратне 11.

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.