Заняття №15-16 на тему «Знаходження раціональних коренів многочлена. Схема Горнера»

Заняття №15-16 на тему «Знаходження раціональних коренів многочлена. Схема Горнера»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 2. Цілі вирази та їх перетворення

Заняття 15 – 16

Знаходження раціональних коренів многочлена. Схема Горнера

Історична довідка

Вільям Джорж Горнер

Вільям Джорж Горнер народився в 1786 році в місті Бристоль в Англії. Отримав освіту в Кінгствудскій школі Бристоля. У віці 14-ти років він став помічником директора в  Кінгствудскій школі  и директором 4 роки по тому. Він поїхав з Бристоля и заснував свою власну школу в 1809 році в Баті.

Суттєвий внесок Горнера в математику – його метод розв’язання  алгебраїчних рівнянь. Його подали на розгляд в Королівське наукове співтовариство 1-го липня 1819 року. Робота була надрукована в тому ж році у Філософських роботах Королівського наукового співтовариства.

В XIX – на початку XX століття метод Горнера займав значне місце в англійських и американських підручниках з алгебри. Виникає питання: для чого він потрібен? Відповідь на це питання дав Де Морган, який показав широкі можливості метода Горнера в своїх  роботах.

Горнер помер 22 вересня 1837 року. Після  смерті Горнера його син, якого теж звали Вільям, продовжив управління школою в Баті.

Для ділення многочленів використовують схему Горнера. Треба розташувати многочлени за спадними степенями х.

Нехай треба поділити многочлен  на двочлен .

Значення а двочлена, коефіцієнти многочлена частки ()та остачу запишемо в наступній  формі:

Якщо будь-який степінь х у многочлені відсутній, то відповідний коефіцієнт дорівнює нулю.

Знайшовши коефіцієнти за схемою, записуємо частку

, якщо R=0, та результат ділення

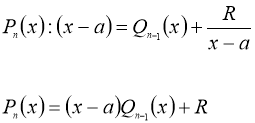
Якщо R≠0.

Розв'язування задач і вправ.

•             Поділити 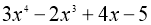на

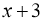
Розв’язання. Згідно із схемою Горнера, запишемо

Отже, () : ()=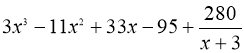, або

=: ():()+280.

•             Користуючись схемою Горнера, поділити многочлени над множиною цілих чисел: 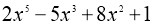на .

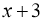Розв’язання: Запишемо схему Горнера: . У схему записуватимемо остаточні результати.

•             Поділити многочлен 4х³-х⁵+32-8х²  на   х+2.

Розв'язання.

Канонічний вид даного многочлена:

-х⁵+0∙х⁴+4х³-8х²+0·х+32.

Отже, частка дорівнює –х⁴+2х³-8х+16.

Завдання для самостійного розв’язування.

1. Для яких значень а і  :

а) многочлен х⁴-3х³+3х²+ах+в  ділиться на х²-3х+2;

б) многочлен х⁴+6х³+5х²+ах+в  ділиться на х²-3х+4;

в) многочлен х⁴-2х³+ах+2  ділиться на х²+х+в.

2. Довести, що многочлен -5х²+4х—4  є дільником многочлена  5х⁴-9х³-2х²+4х-8.
3. Визначити остачу від ділення многочленів:

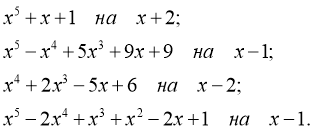
 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.