Заняття №19-20 на тему «Виділення квадрата двочлена. Знаходження найбільшого і найменшого значення виразу»

Заняття №19-20 на тему «Виділення квадрата двочлена. Знаходження найбільшого і найменшого значення виразу»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

 

Тема 2. Цілі вирази та їх перетворення

Заняття 19 – 20

Виділення квадрата двочлена.

Знаходження найбільшого і найменшого значення виразу

Метод виділення повного квадрата заснований на використанні формул квадрата двочлена.

Виділення повного квадрата — це таке тотожне перетворення, за якого заданий тричлен представляється у вигляді суми або різниці квадрата двочлена та деякого числа чи числового виразу.

Розглянемо приклад.

•             Розв'язати рівняння

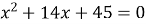
Розв’язання.

Розкладемо многочлен на множники методом виділення повного квадрата. Для застосування першої формули квадрата двочлена необхідно отримати вираз . Тому додамо й віднімемо від даного многочлена число 4, щоб виділити повний квадрат.

,

,

,

.

Застосуємо формулу різниці квадратів: . Маємо:

, то , або , то .

Відповідь:–9;–5.

Розв'язування задач і вправ.

•             Знайти найбільше значення многочлена .

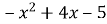Найбільше значення многочлена дорівнює -1 при

•             Знайдіть найменше значення многочлена .

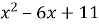Перетворимо даний многочлен .

Найменше значення многочлена дорівнює 2 при

•             Виділіть квадрат двочлена з квадратного тричлена .

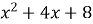Розв’язання. ;

•             Виділіть квадрат двочлена з виразу

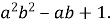
Розв’язання..

•             Виділіть квадрат двочлена з виразу

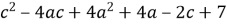
Розв’язання.

•             По конвеєру рухається 10 деталей. Вздовж конвеєра розташовано ряд робочих місць. На першому робочому місці знімається 3 деталі, а на кожному наступному на 2 деталі більше, ніж на попередньому робочому місці. Крім цього, на кожному робочому місці конвеєра поступає додатково 13 деталей. Яка найбільша кількість деталей може бути на конвеєрі і на якому робочому місці?

Розв’язання: 1). Нехай на х-му місці найбільша кількість деталей.

2). З конвеєра зняли деталей.

3). Ще поступило 13х деталей.

4). Загальна кількість деталей:

Відповідь: На 5 чи 6 робочих місцях буде найбільша кількість деталей, що становлять 40 штук.

•             Визначити коефіцієнт квадратного тричлена ax²+bx+c, знаючи, що його найбільше значення дорівнює 25 при 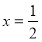і що сума кубів його коренів дорівнює 19.

Розв’язання:

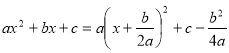•             . Тричлен має найбільше значення 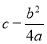при .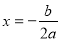

За умовою ;

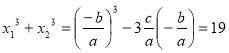
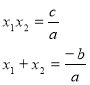
(За теоремою Вієта)

; ; ; ;

Відповідь: с = 24; b = 4; a=-4.

Завдання для самостійного розв’язування.

1. Виділіть квадрат двочлена з квадратного тричлена:

1. ,
2. ,
3. ,
4. ,
5. ,
6. .

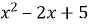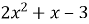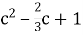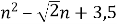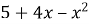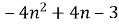2. При якому значенні значення тричлена найменше:

1. ,
2. ,
3. .

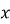
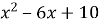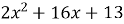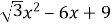3. При яких значеннях значення даного виразу найбільше. Обчисліть це значення, якщо:

1. ,
2. .

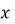
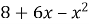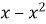4. Знайдіть відстань між найближчими точками осі і графіка функції

 

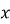
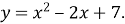
 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.