Заняття №17-18 на тему «Розкладання многочленів на множники. Розв'язування рівнянь методом розкладання многочленів на множники»

Заняття №17-18 на тему «Розкладання многочленів на множники. Розв’язування рівнянь методом розкладання многочленів на множники»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 2. Цілі вирази та їх перетворення

Заняття 17- 18

Розкладання многочленів на множники.

Розв’язування рівнянь методом розкладання многочленів на множники

Рівняння виду , де п- степінь рівняння , а_п, а_п-1, а_п-2,,…, а_1, а₀ – будь-які дійсні числа, причому , називають рівнянням вищого степеня.

Оскільки в лівій частині рівняння вищого степеня стоїть многочлен п-го степеня, то питання про розв'язування рівняння, тобто знаходження його коренів, зводиться до знаходження коренів многочлена .

Для розв'язування рівняння можна розкласти на множники. Цей процес базується на застосуванні теореми Безу.

Розв'язування задач і вправ.

•             Розв’язати рівняння: х³-6х²+11х-6=0.

Розв'язання.

Оскільки а_п=1, то цілі корені рівняння  будемо шукати  серед дільників вільного члена -6, тобто серед чисел: . Оскільки Р(1)=0, то многочлен, що стоїть у лівій частині рівняння, ділиться без остачі на х-1. Скориставшись схемою Горнера, знижуємо степінь многочлена (а отже, і рівняння):

Нове рівняння набирає вигляду х²-5х+6=0. Тому .

•             Розв’язати рівняння: 4х³+8х²+5х+3=0.

Розв'язання.

Перший спосіб.

Дільники вільного члена р: дільники старшого коефіцієнта q: Раціональні корені шукаємо серед чисел :

.; ;; ;;;;;;.

Отже, - корінь. Понизимо степінь многочлена за допомогою схеми Горнера:

Нове рівняння набирає вигляду 4х²+2х+2=0,

3х²+х²+2х+1+1=3х²+(х+1)²+10.

Отже, більше коренів не має, - єдиний корінь.

Другий спосіб.

Введемо заміну 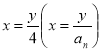. Матимемо:

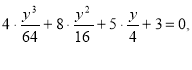
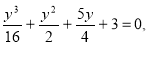
у³+8у²+20у+48=0,

у=-6 – один із коренів. Скористаємося схемою Горнера:

Нове рівняння набирає вигляду

у²+2у+8=у²+2у+1+7=(у+1)²+70.

Тому у=-6 – єдиний корінь, звідки

Завдання для самостійного розв’язування.

Розв’язати рівняння:

1. х³+2х²-х-2=0,
2. х⁴-2х³-11х²+12х+36=0,
3. ,
4. ,
5. ,
6. .

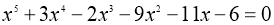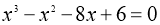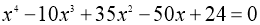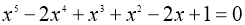 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.