Заняття № 28 «Коло дев’яти точок. Пряма Ейлера»

Заняття № 28 «Коло дев’яти точок. Пряма  Ейлера»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Заняття 28

Коло дев’яти точок. Пряма Ейлера

Теорема. У трикутнику точка перетину медіан, ортоцентр і центр описаного кола лежать на одній прямій.

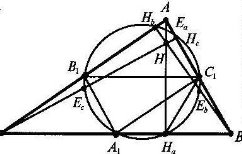В 1765 році Ейлер довів, що в будь-якому трикутнику ортоцентр, барицентр і центр описаного кола лежать на одній прямій. В 20-х роках 19ст. французькі математики Ж.Понселе, Ш. Бріаншон та інші встановили незалежно один одного слідуючу теорему:

ТЕОРЕМА.

У трикутнику основи медіан, основи висот і точки, які поділяють навпіл відрізки, що сполучають вершини трикутника з ортоцентром, лежать на одному колі.

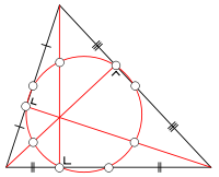Це коло є колом дев’яти точок і називається «колом Ейлера», «колом Фейєрбаха», Фейєрбах встановив, що центр цього кола лежить на «прямій Ейлера».

Коло дев’яти точок — це коло, яке можна побудувати для будь-якого трикутника. Так називається воно через те, що воно проходить через дев’ять важливих точок, шість з яких лежать на самому трикутнику (за винятком тупокутних трикутників). Ці точки:

-середина кожної сторони трикутника

-основа кожної висоти

-середини відрізків, що сполучають вершини трикутника з ортоцентром

Розв'язування задач і вправ.

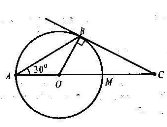
•             Дано коло з центром у точці О. Через точку С, що лежить поза колом, до кола проведено дотичну СВ (В – точка дотику). Січна СО перетинає коло в точці А. Кут ВАС дорівнює 30⁰. Знайти кути трикутника ВОС.

Розв'язання.

1) (за властивістю рівнобедреного трикутника).

2) (за властивістю зовнішнього кута трикутника).

3) (за означенням дотичної).

4) (за властивістю гострих кутів прямокутного трикутника).

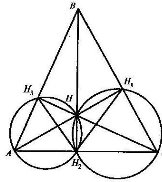
•             Довести, що висоти АН₁, ВН₂, СН₃  гострокутного трикутника АВС поділяють навпіл кути трикутника Н₁Н₂Н₃.

Розв'язання.

Оскільки , то навколо чотирикутника АН₃НН₂ можна описати коло.

Тоді як вписані, що спираються на одну дугу. Аналогічно доводимо, що .

Але , тому що вони доповнюють кут АВС до 90⁰. Звідси . Так само доводимо, що і .

•             На медіані АМ трикутника АВС узято точку К так, що 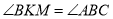. Довести, що .

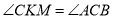Розв'язання.

Продовжимо медіану АМ на відстань, що дорівнює її  довжині.

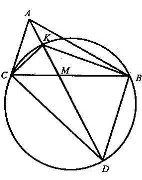
. Отже, точки С, К, В, Д лежать на одному колі. Тоді (як кути, що спираються на дугу СД), але . Звідси .

•             Довести, що квадрат бісектриси трикутника дорівнює різниці між добутком сторін, між якими вона проходить, і добутком відрізків третьої сторони, на які її поділяє бісектриса.

Розв'язання.

Навколо трикутника АВС опишемо коло і продовжимо бісектрису СД трикутника до перетину з колом у точці Е.

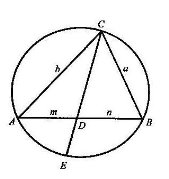Нехай ВС=а, АС=в, АД=т, ВД=п, СД=у, ДЕ=х.

За умовою , крім того, як вписані кути, що спираються на одну дугу. Отже, трикутники АСЕ  і ВСД подібні, і справедлива рівність звідки

у²=ав-ух.Хорди АВ і СЕ перетинаються в точці Д. Тому виконується рівність ух=тп.  Отже, у²=ав-тп.

Завдання для самостійного розв’язування.

1. Усередині трикутника АВС узято довільну точку О. З неї проведено перпендикуляри ОМ, ОF, ∙P на сторони АВ, ВС, АС відповідно. Довести, що .
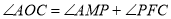2. Дано прямокутний трикутник АВС (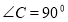) . На його гіпотенузі побудовано квадрат ABFD, М – його центр. Довести, що .

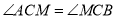Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.