Заняття № 30 «Розв’язування задач на побудову методом геометричних місць»
Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.
Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.
Заняття № 30 «Розв’язування задач на побудову методом геометричних місць»
Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.
Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.
Заняття 30
Розв’язування задач на побудову методом геометричних місць
Найбільша кількість задач на побудову розв’язується методом геометричних місць.
Геометричним місцем точок називається фігура (сукупність або множина точок), що складається з усіх тих і тільки тих точок, які мають певну властивість, або певні властивості.
Геометричне місце точок визначається властивістю (або властивостями) своїх точок. Може трапитися, що задача на побудову зводиться до побудови такої точки (точок), яка має дві властивості, однією з яких визначається одна лінія (наприклад, пряма), а другою – інша лінія (наприклад, коло). Точка перетину цих ліній матиме обидві властивості, а отже, буде шуканою. Побудова такої точки може привести до розв'язання задачі.
Суть методу геометричних місць полягає в слідуючому:
- Вивчивши умову задачі, знаходять таке її обмеження, після відкидання якого останніми визначається деяке ГМТ. Будують його( фігуру f1).
- Приймають до уваги відкинуте раніше обмеження, але знаходять і відкидають таке інше, щоб останніми теж визначалось деяке ГМТ – f2. Будують його. Спільна точка фігур f1 і f2 матиме обидві властивості, а отже, буде шуканою.
Є задачі, в яких точка перетину фігур f1 і f2 є шуканою. Однак в багатьох випадках вона може бути допоміжною, тобто такою, з допомогою якої будується шукана фігура. В окремих задачах шукана точка може належати заданій в умові задачі фігурі (прямій або колу). В такому випадку для побудови цієї точки досить побудувати одне ГМТ.
При розв’язуванні задач на побудову методом геометричних місць дослідження, як правило, пов’язують з існуванням точки перетину фігур f1 і f2 .
Розв'язування задачі вправ.
- Побудуйте трикутник за стороною, медіаною, проведеної до цієї сторони і радіусом описаного кола.
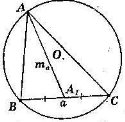
АНАЛІЗ. Нехай трикутник АВС – шуканий, вписаний в дане коло (О,R), ВС=а, ВА1=А1С, АА1=та. Вершина А належить колу (О,R), і колу (А1, та). Звідси, побудова.
ПОБУДОВА.
- Фіксуємо на колі (О,R) довільну точку В.
-
 С=(О,R)
С=(О,R)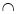 (В, а).
(В, а).
- Будуємо точку А1.
-
А=(О,R)
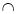 (А1, та).
(А1, та).
ДОВЕДЕННЯ. Випливає з аналізу.
 ДОСЛІДЖЕННЯ. Внаслідок побудови 2 отримаємо дві точки С та С1, якщо
ДОСЛІДЖЕННЯ. Внаслідок побудови 2 отримаємо дві точки С та С1, якщо ![]() . Відрізки ВС і ВС1- рівні. Точка А1 існує, і до того ж, єдина. Якщо кола (А1, та) і (О,R) не мають спільних точок, то задача розв’язків не має. Якщо ці кола дотикаються, то трикутник АВС – рівнобедрений. Задача має єдиний розв’язок, бо трикутник, побудований аналогічно до трикутника АВС на відрізку ВС1 буде рівний з ним. Якщо вказані кола мають дві спільні точки, то отримаємо два рівних трикутники – АВС та А1ВС. В цьому випадку отримаємо чотири рівних трикутника – АВС і А1ВС, і два, рівних з ними, побудованих на хорді ВС1. Оскільки задача метрична, то і в цьому випадку вона буде мати єдиний розв’язок.
. Відрізки ВС і ВС1- рівні. Точка А1 існує, і до того ж, єдина. Якщо кола (А1, та) і (О,R) не мають спільних точок, то задача розв’язків не має. Якщо ці кола дотикаються, то трикутник АВС – рівнобедрений. Задача має єдиний розв’язок, бо трикутник, побудований аналогічно до трикутника АВС на відрізку ВС1 буде рівний з ним. Якщо вказані кола мають дві спільні точки, то отримаємо два рівних трикутники – АВС та А1ВС. В цьому випадку отримаємо чотири рівних трикутника – АВС і А1ВС, і два, рівних з ними, побудованих на хорді ВС1. Оскільки задача метрична, то і в цьому випадку вона буде мати єдиний розв’язок.
-
Побудувати відрізок з довжиною
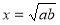 , де а і в – довжини заданих відрізків.
, де а і в – довжини заданих відрізків.
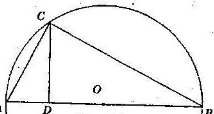
РОЗВ'ЯЗАННЯ. Відомо, що висота прямокутного трикутника, проведена з вершини прямого кута, є середнім геометричним (пропорційним) між відрізками, на які вона поділяє гіпотенузу. Звідси, побудова.
ПОБУДОВА.
- Будуємо послідовно відрізки АД=а і ДВ=в;
- На відрізку АD як на діаметрі будуємо півколо f.
3.Будуємо СД![]() АВ
АВ
(С![]() f) і одержуємо шуканий відрізок СД.
f) і одержуємо шуканий відрізок СД.
Правильність побудови випливає з того, що ![]() .
.
Завдання для самостійного розв’язування.
- Побудуйте трикутник за його бісектрисою і відрізками, на які вона поділяє протилежну сторону.
- Знайти геометричне місце точок, для яких відношення відстаней до двох заданих точок є стала величина.
Використана література
- Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
- Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
- Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
- Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
- Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
- Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
- Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
- Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
- Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
- Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.


про публікацію авторської розробки
Додати розробку
