Заняття № 31 «Класичні задачі, які не розв’язуються за допомогою циркуля та лінійки»

Заняття № 31 «Класичні задачі, які не розв’язуються за допомогою циркуля та лінійки»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Заняття 31

Класичні задачі, які не розв’язуються за допомогою циркуля та лінійки

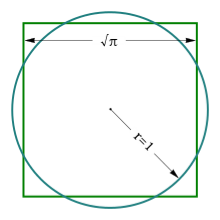З глибокої давнини відомі три задачі на побудову: про подвоєння куба, трисекції кута і квадратури кола. Вони зіграли особливу роль в історії математики. Зрештою було доведено, що ці завдання неможливо розв’язати, користуючись лише циркулем і лінійкою. Але вже сама постановка завдання - «довести нерозв'язність» - була сміливим кроком вперед. Разом з тим пропонувалося безліч розв’язків за допомогою нетрадиційних інструментів. Все це призвело до виникнення і розвитку абсолютно нових ідей в геометрії і алгебри. Чимало досягли успіху в нестандартних і різних наближених розв’язках любителі математики - серед них три знамениті завдання старовини особливо популярні.

Давньогрецькі математики досягли надзвичайно великого мистецтва в геометричних побудовах за допомогою циркуля і лінійки. Однак три завдання не піддавалися їхнім зусиллям.

Квадратура круга — задача, що полягає в знаходженні побудови за допомогою циркуля та лінійки квадрата, рівновеликого за площею до даного круга.

Історія знаходження квадратури кола тривала чотири тисячоліття, а сам термін став синонімом нерозв'язних завдань. Як випливає з подібності кіл, відношення довжини кола до її діаметра є величина постійна, яка не залежить від радіуса кола, вона позначається буквою . Таким чином, довжина кола круга радіуса r дорівнює 2r, а так як площа круга дорівнює , то завдання про квадратуру кола зводиться до задачі побудови трикутника з основою 2r і висотою r. Для нього потім вже без зусиль може бути побудований рівновеликий квадрат.

Отже, завдання зводилося до побудови відрізка, довжина якого дорівнює довжині кола даного кола. Це було показано ще Архімедом у творі «Вимірювання круга», де він доводить, що число менше ніж 4,але більше ніж 3тобто 3,1408.

У наші дні за допомогою ЕОМ число обчислено з точністю до мільйона знаків, що являє швидше технічний, ніж науковий інтерес, тому що така точність нікому не потрібна. Десяти знаків числа (=3,141592653 ...) цілком достатньо для всіх практичних цілей. Довгий час в якості наближеного значення використовували число 22/7, хоча вже в V ст. в Китаї було знайдено наближення 355/113 == 3,1415929 ..., яке було відкрито знову в Європі лише в XVI в. У Стародавній Індії вважали рівним 3,1622.... Французький математик Ф. Вієт обчислив 1579 р з 9 знаками. Голландський математик Лудольф Ван Цейла в 1596 р публікує результат свого десятирічного праці - число , обчислене з 32 знаками.

Але всі ці уточнення значення числа вироблялися методами, зазначеними ще Архімедом: коло замінювалося многокутником з дедалі більшим числом сторін. Периметр вписаного многокутника при цьому був менше довжини кола, а периметр описаного многокутника - більше. Але при цьому залишалося неясним, чи є число раціональним, тобто відношенням двох цілих чисел, або ірраціональним. Лише в 1767 р німецький математик І. Г. Ламберт довів, що число ірраціональне, а ще через сто з гаком років в 1882р інший німецький математик – Ф. Ліндеман довів його трансцендентність, що означало і неможливість побудови за допомогою циркуля і лінійки квадрата, рівновеликого даному колу.

Звичайно, способів наближеного розвязання квадратури кола за допомогою циркуля і лінійки було придумано безліч. Так, в Стародавньому Єгипті було поширено правило: площа круга дорівнює площі квадрата зі стороною, рівною 8/9; =256/81=3,1604.

Були знайдені й інші шляхи визначення квадратури кола: крім циркуля і лінійки використовували інші інструменти або спеціально побудовані криві. Так, у V ст. до н.е. грецький математик Гиппий з Еліди винайшов криву, що згодом отримала назву квадратриси Дінострата (її назвали по імені іншого давньогрецького математика, який жив дещо пізніше і вказав спосіб побудови квадратури кола за допомогою цієї кривої).

Надзвичайно цікаво, що квадратриса Дінострата розвязує і другу із знаменитих завдань стародавності задачу про трисекцию кута.

Трисекція кута — задача про поділ заданого кута на три рівні частини за допомогою циркуля та лінійки. Інакше кажучи, необхідно побудувати трисектриси кута — промені, що ділять кут на три рівні частини.

П'єр Лоран Ванцель у 1837 році довів, що задача розв'язна тільки тоді, коли розв'язне в квадратних радикалах рівняння:

Хоча трисекція кута в загальному випадку нездійсненна за допомогою циркуля і лінійки, існують криві, за допомогою яких цю побудову можна здійснити. Равлик Паскаля або трисектриса, Квадратриса (в давнину також називалась трисектрисою), Конхоїда Нікомеда, Конічні перетини, Спіралі Архімеда.

До кубічного рівняння зводиться і знаменита задача подвоєння куба. Згідно з античною легендою, одного разу на острові Делос почалася епідемія чуми. Мешканці острова звернулись до дельфійського оракула, і той повідомив, що необхідно подвоїти жертовне святилище, яке мало форму куба. Мешканці Делоса спорудили ще один такий же куб та поставили його на перший, але епідемія не припинилася. Після повторного звернення оракул роз'яснив, що подвоєний жертовник також повинен мати форму куба.

Завдання про подвоєння куба виявилася набагато важчим. Гіппократ Хіоський (кінець V ст. до н. е.) показав, що задача зводиться до знаходження двох середніх пропорційних між одним відрізком та іншим, вдвічі більшим за нього. У сучасних позначеннях — до знаходження та таких, що . Звідси ..

Архіт Тарентський (початок IV ст. до н. е.) запропонував розв'язок, заснований на перетині тора, конуса та кругового циліндра.

Платон (перша половина IV ст. до н. е.) запропонував механічний розв'язок, заснований на побудові трьох прямокутних трикутників з потрібним співвідношенням сторін.

Менехм (середина IV ст. до н. е.) знайшов два розв'язки цієї задачі, засновані на використанні конічних перетинів. У першому розв'язку відшукується точка перетину двох парабол, а у другому — параболи та гіперболи.

Ератосфен (III ст. до н. е.) запропонував ще один розв'язок, в якому використовується спеціальний механічний інструмент — мезолябія, а також описав розв'язок своїх попередників.

Нікомед (II ст. до н. е.) використовував для розв'язку цієї задачі метод вставки, яка виконується за допомогою спеціальної кривої — конхоїди.

Група схожих між собою розв'язків, які належать Аполлонію, Філону Візантійському та Герону, також використовує метод вставки.

У ще одній групі схожих між собою розв'язків, які належать Діоклу, Паппу та Спору, використовується та ж ідея, що і у розв'язку Платона, при цьому Діокл застосовує для побудови спеціальну криву — цисоїду.

Свої розв'язки також запропонували Вієт, Декарт, Грегуар де Сен-Венсан, Гюйгенс, Ньютон.

У сучасних позначеннях, задача зводиться до розв'язку рівняння . Розв'язок має вигляд . Все зводиться до проблеми побудови відрізка довжиною .

Ванцель довів у 1837 році, що ця задача не може бути розв'язана за допомогою циркуля та лінійки.

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.