Заняття № 29 «Побудова за допомогою циркуля та лінійки»

Заняття № 29 «Побудова за допомогою циркуля та лінійки»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Заняття 29

Побудова за допомогою циркуля та лінійки

Побудова за допомогою циркуля та лінійки — розділ евклідової геометрії, відомий ще з античних часів.

В задачах на побудову можливі такі операції:

• Позначити довільну точку на площині, точку на одній з побудованих ліній або точку перетину двох побудованих ліній.
• За допомогою циркуля намалювати коло з центром в побудованій точці та радіусом, рівним відстані між двома вже побудованими точками.
• За допомогою лінійки провести пряму, що проходить через дві побудовані точки.

При цьому циркуль та лінійка вважаються ідеальними інструментами, зокрема:

Лінійка не має поділок і має тільки одну сторону нескінченної довжини;

Циркуль може мати який завгодно великий радіус.

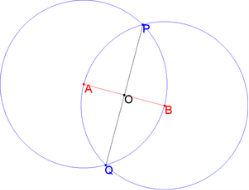
Задача. За допомогою циркуля та лінійки поділити даний відрізок AB на дві рівні частини. Один з розв'язків показано на малюнку:

Циркулем будуємо коло з центром в точці A радіусу AB.

Будуємо коло з центром в точці B радіусу AB.

Знаходимо точки перетину P та Q двох побудованих кіл.

Лінійкою проводимо відрізок, з'єднуючий точки P та Q.

Знаходимо точку перетину AB та PQ. Це — шукана середина відрізка AB.

Античним геометрам були відомі методи побудови деяких правильних n-кутників.

Гаус у 1796 р. показав можливість побудови правильних n-кутників при , де — різні прості числа Ферма. У 1836 р. П. Ванцель довів, що інших правильних багатокутників, які можна побудувати циркулем та лінійкою, не існує.

Побудови за допомогою одного циркуля. За теоремою Мора — Маскероні за допомогою одного циркуля можна побудувати будь-яку фігуру, яку можна побудувати циркулем та лінійкою. При цьому пряма вважається побудованою, якщо на ній задано дві точки.

Побудови за допомогою однієї лінійки. Легко помітити, що за допомогою однієї лінійки можна реалізувати тільки проективно-інваріантні побудови. Зокрема, неможливо навіть розбити відрізок на дві рівні частини або знайти центр намальованого кола. Але за наявності на площині заздалегідь проведеного кола з позначеним центром за допомогою лінійки можна провести ті ж побудови, що і циркулем та лінійкою (теорема Понселе - Штейнера (англ.)), 1833.

Цікаво, що візерунок на прапорі Ірану описується як побудова за допомогою циркуля та лінійки

Розвязування задач та вправ.

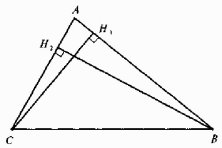
•             Побудуйте трикутник ABC за кутом А і висотами hb і hc.

Розв'язання

Побудуємо прямокутний трикутник АН2В з катетом ВН2 = hb і гострим кутом А. Дістанемо сторону АВ. Потім будуємо прямо­кутний трикутник АСНг з гострим кутом А і катетом  СН3 = hc. Дістанемо сторону АС. Трикутник ABC — шуканий.

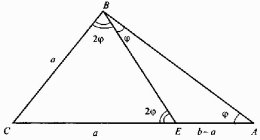
•             Побудуйте, циркулем і лінійкою трикутник за двома даними сторонами a і b (b > a), якщо відомо, що кут проти однієї з них втричі більший від кута проти другої.

Розв'язання

Припустимо, що трикутник ABC побудовано, B=3A. Проведемо з точки В до прямої АС відрізок BE такий, що ABE = BAC. Тоді трикутник ВСЕ буде рівнобедреним, тому  АЕ = ВЕ. Трикутник ВСЕ також рівнобедрений, оскільки BEC = CBE = 2 BAC, тому ВС = СЕ = а. Отже, АЕ = ЕВ = b–а, оскільки АС = b.

У трикутнику ВСЕ СВ = СЕ – а, ЕВ = b – а, тому його можна побудувати, користуючись циркулем і лінійкою. Після цього на продовженні сторони СЕ відкладемо відрізок ЕА = b – а. Трикутник ABC — шуканий.

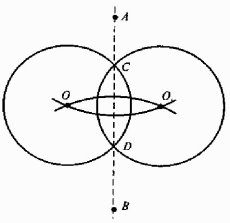
•             Дано коло і його центр О. Точки А і В лежать поза колом. Побудуйте, користуючись лише циркулем, точки перетину даного кола з прямою АВ.

Розв'язання

Візьмемо пряму АВ за вісь симетрії і побудуємо коло, симетричне даному. Його центр — точка перетину кіл з центрами в точках А і В та радіусами відповідно АО і ВО. Перетин цього кола з даним — шукані точки С і D.

Завдання для самостійного розв’язування.

1. Побудуйте квадрат з даним центром О, якщо дві паралельні сторони квадрата (або їх продовження) проходять через дані точки М і N (пряма MN не містить точки О).
2. Побудуйте трикутник за кутом В, стороною а, та сумою сторін b + с.
3. Побудуйте трикутник за сторонами а, b та бісектрисою lс.

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.