Заняття № 32 «Розв’язування олімпіадних задач»

Заняття № 32 «Розв’язування олімпіадних задач»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Заняття 32

Розв'язування олімпіадних задач

Розглянемо деякі задачі на побудову.

•            Розглянемо задачу: "Земельна ділянка квадратної форми була обгороджена. Від огорожі збереглися два стовпи на паралельних сторонах квадрата. Крім того, залишився стовп у центрі квадрата. Потрібно відновити границю ділянки".

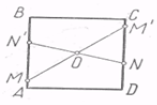Аналіз. Нехай ABCD — шуканий квадрат, О — його центр, М і N- дані точки відповідно на сторонах АВ і CD . Якщо повернути квадрат на 180° близько його центру О, то він перетвориться сам у себе. Точка М займе деяке положення М' на стороні CD, а точка N — деяке положення N' на стороні АВ. Після цього неважко вже побудувати прямі АВ і CD і відновити шуканий квадрат.

Побудова. 1) Будуємо точку М', симетричну М відносно О, і точку N', симетричну N відносно О. 2) Будуємо прямі MN' і NM'. 3) Повернемо побудовані прямі близько точки О на 90°. Чотири побудовані прямі обмежують шуканий квадрат.

Доказ опускаємо.

Дослідження. За змістом задачі неможливий випадок, коли точки М і N розташовуються із точкою О на одній прямій, але не симетричні відносно О. Якщо точки М і N симетричні відносно О, то задача стає невизначеною. В інших випадках задача має єдиний розв'язок .

•             Розглянемо задачу: "Побудувати опуклий чотирикутник, знаючи три його кути й дві протилежні сторони".

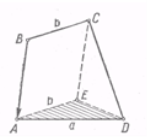Докладніше: дано два відрізки а й b і три кути б, в, д. Потрібно побудувати чотирикутник ABCD так, щоб А = б, В = в, D = д, AD = a, СВ = b. Передбачається, що 0° < б < 180, 0° < в < 180, 0°< д < 180°.

Аналіз. Допустимо, що ABCD— шуканий чотирикутник. Перенесемо сторону ВС на вектор, і нехай відрізок ВС займе після переносу положення АЕ. Тоді в AED відомі: AD = a, AE = b, DAE = BAD – BAE = A – (180° – B) = б + в – 180°. За цим даними AED може бути побудований.

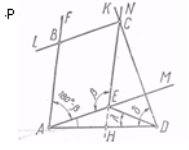Побудова. 1) На довільній прямій будуємо відрізок AD = а ; 2) Через точку А проводимо промінь AM під кутом б + в – 180° до променя AD; 3) Відкладаємо на промені AM відрізок АЕ = b; 4) Будуємо промінь EN, що утворює з ЕА кут в й розташований із точкою D по різні сторони від прямої AM; 5) Будуємо промінь DK так, щоб ADK був рівний д і щоб промінь DK розташовувався по ту ж сторону прямщї DE, що й промінь EN; 6) Відзначаємо точку С перетинання променів EN і DK — третю вершину чотирикутника; 7) Четверта вершина В знаходиться з перитинання прямої AF, паралельної СE, із прямої CL, паралельної АЕ.

Доказ. BAD = ВАЕ+ DAE = (180° – в) + (б + в – 180°) = б. ABC = СЕА, як кути, сторони яких відповідно паралельні й протилежно спрямовані. СЕА = в за побудовою. ADC = д за побудовою. Відрізок AD = а за побудовою. Але АЕ = b, а виходить, і ВС = b .

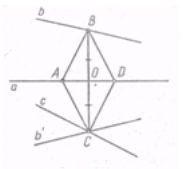•             Розглянемо задачу: "Побудувати ромб так, щоб одна з його діагоналей дорівнювала даному відрізку r і лежала на даній прямій а, а інші дві вершини ромба лежали відповідно на даних прямих b і с".

Аналіз. Нехай ABDC — шуканий ромб, AD = r. Зауважемо, що задача про побудову ромба зводиться до побудови однієї якої-небудь із його вершин, наприклад вершини С. За властивостями ромба точки В и С симетричні відносно прямої а. Тому при осьовій симетрії відносно прямої а точка В перетвориться в точку С, а, отже, пряма b — у деяку пряму b', що проходить через точку С. Таким чином, точка С може бути побудована як точка перетину прямих с і b', з яких одна дана, а інша легко будується.

Побудова. Будуємо послідовно: пряму b', симетричну із прямій b відносно прямої а; точку С, загальну для прямих с і b'; пряму ВС; точку ОВС а; точки А и D на прямій а, що знаходяться від точки О на відстані ; ABCD — шуканий ромб. Дослідження. Можливі наступні випадки: 1) с || b', розв'язків немає; 2) с b', розв'язків нескінченно багато; 3) прямі с і b' перетинаються поза прямою а, один розв'язок; 4) прямі с і b' перетинаються на прямій а, розв'язків немає .

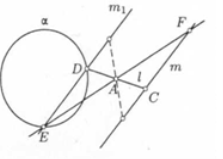•             Розглянемо задачу: " Через дану точку А провести пряму так, щоб її відрізок з кінцями на даних прямій і окружності ділився точкою навпіл".

Розв'язок. Нехай m і б — дані пряма й окружність, CD - шуканий відрізок, С m, Dа. Тоді (C) = D. Якщо (m) = m₁, то Dm₁ і, отже, Dа m₁. Звідси випливає така побудова: будуємо образ m₁ прямій m при симетрії , крапки D і Е перетинання прямій m₁ з даною окружністю б визначають разом із крапкою А шукані прямі DA і ЕА .

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.