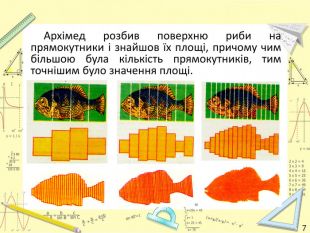
Заняття на тему: "Визначений інтеграл"
Під час заняття використано техніку "ажурна пилка". Ажурна пилка - це техніка групової роботи, яка допомагає активізувати всіх учасників. Кожен здобуває інформацію завдяки самостійній роботі з першоджерелами та співпраці з іншими учасниками. Така організація роботи дозволяє залучити слабших студентів або таких учасників, які невпевнено почувають себе в групі. Дану техніку варто використовувати при введенні нових тем або на підсумкових заняттях. Вона вчить вибирати із тексту головний зміст і відповідати за успіх групової роботи.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
МОГИЛІВ – ПОДІЛЬСЬКИЙ ТЕХНОЛОГО-ЕКОНОМІЧНИЙ КОЛЕДЖ
ВІННИЦЬКОГО НАЦІОНАЛЬНОГО АГРАРНОГО УНІВЕРСИТЕТУ
ТЕМА. ВИЗНАЧЕНИЙ ІНТЕГРАЛ
ТА ЙОГО ЗМІСТ
методична розробка відкритого заняття
з дисципліни «Вища математика»
2017
Автор Останіна Юлія Володимирівна, викладач математики,
спеціаліст першої категорії
Рецензент Кордонська Ірина Василівна, викладач математики,
спеціаліст вищої категорії, методист
Методична розробка заняття розкриває
творчий досвід викладача щодо оновлення
навчально – виховного процесу.
На занятті використані різноманітні
форми роботи з групою: фронтальна бесіда,
самостійна робота, тренувальні вправи,
ілюстрації, елементи ігрових технологій
Рекомендовано для викладачів навчальних
закладів I-II рівнів акредитації
Розглянуто і схвалено на засіданні
циклової комісії природничо – наукових
та загальноекономічних дисциплін
Протокол № ___ від _________2017
Голова ц/к ____________/Носкова Т.А./
Інтенсивні зміни, які відбуваються в даний час в нашому суспільстві, вимагають творчо розвиненої, креативно мислячої, компетентної, активної особистості, орієнтують педагогів на новий рівень викладання і виховання студентів.
Якщо в недавньому минулому основним завданням, що стоїть перед викладачем, була передача студентам певної суми знань, то в даний час на перший план висувається завдання розвитку творчого мислення студентів в процесі навчання, вміння ними самостійно поповнювати свої знання, орієнтуватися в стрімкому потоці сучасної наукової інформації, розвивати їх здатність адаптуватися до постійно мінливих життєвих ситуацій, шукати шляхи нестандартного вирішення ситуацій і проблем.
Загальновизнано, що математика є найбільш трудомістким навчальним предметом, що вимагає від студентів постійної, кропіткої і значної за обсягом самостійної роботи. Тому одним з головних завдань викладача математики, є формування і розвиток навичок вивчення математики, елементів культури навчання і мислення через використання інноваційних та інформаційних технологій навчання, які допоможуть студентам краще засвоїти необхідні компоненти програми навчання, дозволять розвивати пізнавальні інтереси студентів, їх активність у навчальній діяльності, а також забезпечать формування і розвиток комунікативних якостей студентів.
Дуже важливе для викладача завдання – навчити всіх дітей самостійно отримувати знання, а цього можна досягти шляхом схильності студента до творчого сприйняття навчального матеріалу і його бажання самостійно подолати труднощі, що виникають. Цьому значною мірою сприяють різні види і форми самостійної роботи, нестандартні прийоми навчання, інтерактивні форми роботи на заняттях. Великі можливості представляє самостійна робота під час розв’язання задач і вправ на заняттях. Викладач має орієнтуватися на всіх студентів групи, маючи на увазі загальні знання в цілому і кожного студента окремо. Такий підхід спонукає до роботи і сильного студента, і слабого.
Ажурна пилка
Опис техніки навчання
Ажурна пилка - це техніка групової роботи, яка допомагає активізувати всіх учасників. Кожен здобуває інформацію завдяки самостійній роботі з першоджерелами та співпраці з іншими учасниками. Така організація роботи дозволяє залучити слабших студентів або таких учасників, які невпевнено почувають себе в групі. Дану техніку варто використовувати при введенні нових тем або на підсумкових заняттях. Вона вчить вибирати із тексту головний зміст і відповідати за успіх групової роботи.
Спосіб проведення занять
1. Ведучий об’єднує учасників y команди. Слід створити стільки команд, на скільки частин вдалось поділити матеріал, з яким вони працюватимуть. Однак найоптимальніший варіант – стільки команд, скільки учасників групі. Кожен член команди отримує свій номер. Цей номер вкаже йому команду, в якій він працюватиме y наступному етапі. (5 хвилин)
2. Ведучий роздає поділений на частини текст. Команда І отримує першу частину, ІІ – другу частину, ІІІ – третю, і так далі. (5 хвилин)
3. Кожен учасник спочатку самостійно ознайомлюється з текстом. Підкреслює в ньому те, що вважає за найбільш істотне. Після цього група розмовляє на тему прочитаного тексту і спільно визначає головний зміст. Студенти можуть робити нотатки, записуючи головний зміст.(15 хвилин)
4. Після цього учасники переходять до нових команд (експертних команд), кожна з яких складатиметься з одного представника першого складу команд. Експерти розповідають про те, чого вони навчились y своїх попередніх командах. Члени команд уважно слухають кожного експерта по черзі, роблять нотатки. (15-30 хвилин)
5. Всі повертаються до своїх попередніх груп і під час розмови на тему опрацьованого тексту виконують конспект, який ілюструє цілий обсяг матеріалу. (15 хвилин)
6. На завершення з метою перевірки рівня засвоєння матеріалу, можна запропонувати учасникам короткий тест. (10 хвилин)
На що треба звертати увагу:
1. Культура розмови – вчитель повинен піклуватися, щоб розмова не викликала негативних емоцій, а також, щоб групові рішення приймалися під впливом змістовних аргументів.
2. Склад групи – треба слідкувати, щоб до однієї групи не входили виключно несміливі учні, або особи із схильністю до домінації.
Дисципліна: Математика.
Дата: 20.11.2017р.
Група: КД 15/9-16
Методична мета заняття: застосування інноваційних технологій при вивченні математики з використанням елементів самостійної роботи; розвиток творчої складової в процесі формування вмінь та навичок студентів, застосування активних форм і методів виховання особистості компетентного спеціаліста.
Вид заняття. Інтерактивна лекція
Тема заняття. Визначений інтеграл та його зміст.
Мета.
Навчальна: Поглибити й розширити знання студентів про визначений інтеграл; закріпити навички знаходити визначений інтеграл, показати його місце і значення при розв’язуванні задач фізичного, економічного, геометричного змісту; учити бачити єдину математичну модель у різних ситуаціях, складати її в нестандартних умовах.
Розвиваюча: Вчити студентів досліджувати й оцінювати соціальні явища засобами математики; бачити необхідність планування майбутнього; допомогти сформувати особисте ставлення до діяльності, яка вимагає математичних знань.
Виховна: Виховувати математичну культуру, вміння правильно застосовувати математичну символіку; виховувати інтерес до дисципліни розкриваючи її велике значення для розвитку різних галузей наук та повсякденного життя.
Міжпредметні зв’язки.
Забезпечувані. Фізика. Робота змінної сили.
Математика. Інтегральне числення .
Економіка. Розрахункові задачі на обчислення прибутку,
затрат на виробництво товару, продуктивності праці.
Забезпечення заняття.
1. Література. Ю.Л.Луценко . Вища математика.
М.В.Богомолов. Практичні заняття з математики.
2. Наочні посібники. Таблиці “Основні формули інтегрування”
3. Роздаткові матеріали. Опорні конспекти “Основні формули інтегрування”. Варіанти завдань для самостійної роботи.
4. Обчислювальні засоби. Калькулятор.
Компетенції навчальна, інформаційна, мотиваційно - стимулювальна.
Функції:
Теоретична - Знати: поняття криволінійної трапеції, її площі; поняття
визначеного інтеграла, його геометричний та фізичний зміст;
властивості визначеного інтеграла.
Практична - Вміти: обчислювати визначені інтеграли, площі
криволінійних трапецій.
Хід заняття
1. Організаційна частина заняття
(Метод: психолого – педагогічної підтримки роботи студентів на занятті, рефлексія)2 хв.
1.1 Встановлення психолого – педагогічного контакту з аудиторією студентів.
1.2 Викладач перевіряє готовність студентів до заняття, налаштовує їх на роботу.
Найкращий спосіб вивчити що-небудь — це відкрити самому.
Д. Пойа
2. Підготовка студентів до заняття. (метод: інструктування).
2.1 Повідомлення теми, мети та плану заняття.
Тема заняття: Визначений інтеграл та його зміст.
Мета заняття: Формувати поняття визначеного інтегралу, з’ясувати
геометричний, фізичний та економічний зміст визначеного
інтегралу.
План заняття:
1. Поняття визначеного інтеграла.
2. Геометричний зміст визначеного інтеграла.
3. Фізичний зміст визначеного інтеграла.
4. Економічний зміст визначеного інтеграла.
2.2 Мотивація пізнавальної діяльності студентів (методи: бесіда, навіювання, переконання).
Ми з вами сьогодні спробуємо за допомогою математики розв’язати проблеми, що виникають на заняттях фізики та економіки. Математика здавна має репутацію найточнішої галузі знань і є надійним знаряддям розкриття таємниць природи.
За допомогою визначеного інтегралу обчислюють площі плоских фігур, які називаються криволінійними трапеціями. Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні, оскільки необхідні для ведення різноманітних справ, для гармонійного розвитку галузей виробництва, тощо. У цих науках також використовується поняття інтеграла. Серед них такі як економіка виробництва, фінансова справа, електроніка, програмування, фізика, хімія, радіофізика, тощо.
За допомогою визначеного інтегралу знаходять у фізиці роботу змінної сили, розв’язують задачі економічного змісту на визначення прибутку, затрат.
Анрі Пуанкаре, французький математик, сказав: „Математика є спосіб називати різні речі одним ім’ям”. Можливість розвивати ці уміння ви й матимете сьогодні, розв’язуючи задачі, пов’язані з геометрією, фізичними явищами, економічними процесами. І ви матимете чудову нагоду розвинути і закріпити навички знаходити визначений інтеграл, застосовувати його при розв’язуванні практичних задач.
2.3 Актуалізація опорних знань студентів.( методи – метод „ Мікрофон ",
пояснювально – ілюстративний; форма роботи - презентація, діалог, тестування)
А зараз, відповідаючи на питання, ми налаштуємося на розгляд більш складних проблем.
1. Що таке первісна?
2. Назвіть, будь ласка, формулу Ньютона – Лейбніца.
3. Яка головна відмінність визначеного інтегралу від невизначеного?
4. Нагадати правила інтегрування (інтеграл суми, різниці функцій, винесення сталого множника за знак первісної, інтегрування складеної функції, що залежить від лінійної функції).
А зараз ми ще раз звернемося до інтегралів й перевіримо, як ви вмієте знаходити інтеграл степеневої функції.
Вставте пропущені символи, щоб рівність була правильною.
І варіант. ІІ варіант
![]() = ........+ ... .
= ........+ ... . ![]() = .........+ ... .
= .........+ ... .
![]() =
= ![]() + ... .
+ ... . ![]() =
= ![]() + ... .
+ ... .
![]() = -соs х + С.
= -соs х + С. ![]() = sin х + С.
= sin х + С.
![]() = 8х + С.
= 8х + С. ![]() = 4х + С.
= 4х + С.
![]() =
= ![]() + С.
+ С. ![]() =
= ![]() + С.
+ С.
![]() =
= ![]() = ... .
= ... . ![]() =
= ![]() = ... .
= ... .
Після виконання самостійної роботи студенти перевіряють правильність виконання самостійної роботи, звіряючи написане в зошиті з правильними відповідями.
І варіант. ІІ варіант
![]() = 7x + С .
= 7x + С . ![]() = 5x + С .
= 5x + С .
![]() =
= ![]() + С .
+ С . ![]() =
= ![]() + С .
+ С .
![]() = - соs х + С.
= - соs х + С. ![]() = sin х + С.
= sin х + С.
![]() = 8х + С.
= 8х + С. ![]() = 4х + С.
= 4х + С.
![]() =
= ![]() + С.
+ С. ![]() =
= ![]() + С.
+ С.
![]() =
= ![]() =
= ![]() .
. ![]() =
= ![]() =
= ![]()
3. Вивчення нового матеріал (розповідь з елементами бесіди, пояснення, пояснювально – ілюстративний, опора на життєвий досвід, самостійне вивчення, розв’язання типових вправ).
Технологія «Ажурна пилка»
1. Викладач об’єднує студентів y підгрупи, роздає поділений на частини текст. (5 хвилин)
2. Кожен студент спочатку самостійно ознайомлюється з текстом, підкреслює в ньому те, що вважає за найбільш істотне. Після цього група розмовляє на тему прочитаного тексту і спільно визначає головний зміст. Студенти можуть робити нотатки, записуючи головний зміст.(15 хвилин)
3. Після цього студенти переходять до нових команд (експертних команд), кожна з яких складатиметься із одного представника першого складу команд. Експерти розповідають про те, чого вони навчились y своїх попередніх командах. Члени команд уважно слухають кожного експерта по черзі, роблять нотатки. (15-30 хвилин)
4. Всі повертаються до своїх попередніх груп і під час розмови на тему опрацьованого тексту роблять конспект, який ілюструє цілий обсяг матеріалу. (15 хвилин)
3.1. Визначений інтеграл
Першим відомим методом для розрахунку інтегралів був метод вичерпування Евдокса ( приблизно 370 до н.е.), який намагався знайти площі та об'єми і для цього розривав їх на величезну кількість частин, для яких площа і об'єм вже відомі. Цей метод розвинув Архімед і використав його для розрахунку площ парабол і наближених обчислень площ частин круга.
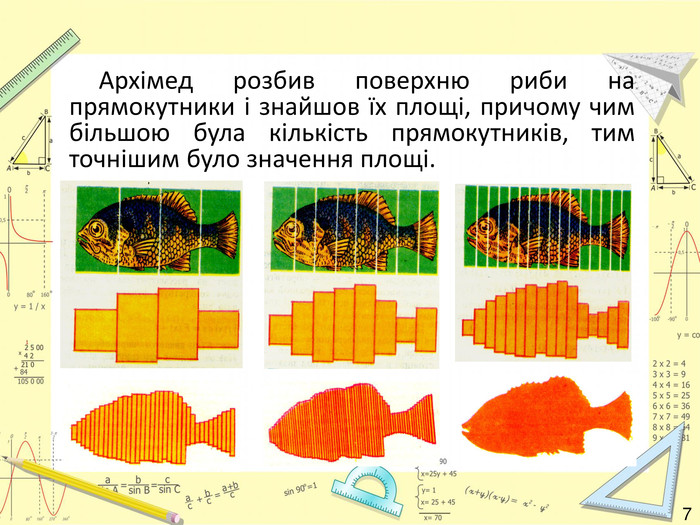
Інтеграл виник з практичної потреби знаходити площі неплоских фігур. Найбільший внесок у вивченні інтегрального числення вніс Архімед. Одного разу Архімед повернувся з риболовлі і вирішив визначити найбільш точно площу поверхні риби. Архімед розбив поверхню риби на прямокутники і знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.
Символ інтеграла ввів Г. Лейбніц 1675р. Слово інтеграл придумав І.Бернуллі. Межі інтегрування вказав Л. Ейлер
Формула Ньютона - Лейбніца
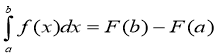
Значний внесок у вивчення поняття інтеграла зробили українські математики
М.В.Остроградський (1801-1862рр.), В.Я.Буняковський (1804-1889рр.),
Д.О.Граве (1863-1939рр.), М.П.Кравчук (1892-1942рр.).
Текст, який опрацьовують студенти самостійно.
3.2. І група Геометричний зміст визначеного інтеграла.
Обчислення площі криволінійної трапеції
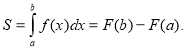 Спосіб обчислення площі криволінійних трапецій походить з далекої давнини. Ще в III ст. до н. е. великий Архімед обчислив площу параболічного сегмента з допомогою відкритого ним ,,методу вичерпування'', який через дві тисячі років був перетворений в метод інтегрування. Однак лише в XVIIст. Ньютону і Лейбніцу вдалось відкрити загальний спосіб обчислення площ за допомогою інтегралів. Ця формула так і називається: формула Ньютона-Лейбніца.
Спосіб обчислення площі криволінійних трапецій походить з далекої давнини. Ще в III ст. до н. е. великий Архімед обчислив площу параболічного сегмента з допомогою відкритого ним ,,методу вичерпування'', який через дві тисячі років був перетворений в метод інтегрування. Однак лише в XVIIст. Ньютону і Лейбніцу вдалось відкрити загальний спосіб обчислення площ за допомогою інтегралів. Ця формула так і називається: формула Ньютона-Лейбніца.
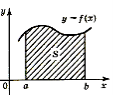
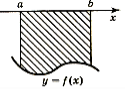
З цієї формули ми можемо зробити висновок, що інтеграл це - ПЛОЩА.
Нехай функція f(x) для всіх значень аргументу x[a,b] є додатною. Тоді інтегральна сума представляє собою сумарну площу прямокутників S1,…,Si,…,Sn (рис. 1). Визначений інтеграл у цьому випадку дорівнює площі криволінійної трапеції, обмеженої кривими y=0, x=a, x=b та y=f(x).
![]() y
y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() y=f(x)
y=f(x)
S1 S2 ……Sn.
0 a x1 x2 ..xn-1 b x
Рис. 1
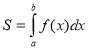
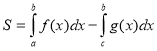
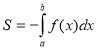
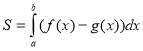
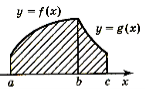
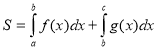
![]() Задача1: Обчислити площу фігури, обмеженої лініями:
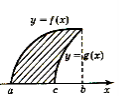
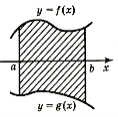
Задача1: Обчислити площу фігури, обмеженої лініями:
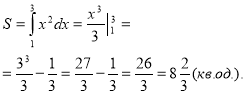
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
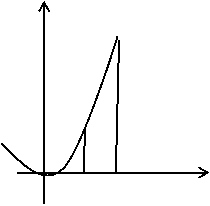
Задача 2 : Знайти площу фігури, обмежену графіком функції ![]() , віссю абсцис та прямими x=1 , x=9
, віссю абсцис та прямими x=1 , x=9
![]() .
.
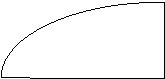
![]() y
y
![]()
![]()
![]()
1 9 x
3.2. ІІ група Геометричний зміст визначеного інтеграла.
Обчислення об’ємів тіл
Задача про обчислення об’єму тіла розв’язується аналогічно до задачі про площу криволінійної трапеції.
Нехай задано тіло Т і координатна пряма Ох у просторі. Проведемо площини, перпендикулярні до прямої Ох так, щоб вони перетинали тіло Т або дотикались до нього.
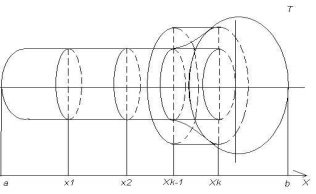
Дотичні площини, що обмежують тіло, перетнуть вісь Ох у точках а і b, а будь-яка площина між ними перетне її в точці х. Позначимо площу перерізу тіла цією площиною через S. Кожному значенню х з відрізка [a; b] відповідатиме певне значення площі перерізу S = S(x). Площина перерізу буде відтинати тіло, об’єм якого є також функцією х, тобто V = V(x). Тому можна стверджувати, що на відрізку [a; b] визначена функція S(x). Якщо вона неперервна на відрізку [a; b], то функція V(x) є первісною для функції S(x) і справджується формула 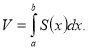
Обчислення об’єму тіла, утвореного обертанням графіка функції навколо осі Ох: V = 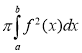 .
.
Обчислення об’єму тіла, утвореного обертанням графіка функції навколо осі Оу: V = 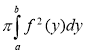 .
.
Приклад 1. Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої синусоїдою і прямими х = 0, ![]()
Розв’язання
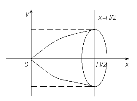
Відповідь: ![]()
Приклад 2. Знайти об’єм тіла, утвореного обертанням навколо осі Оу фігури, обмеженої прямими: у = 2х, х = 0, у = 5.
Розв’язання
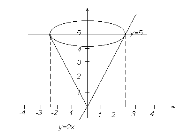
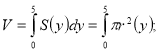
![]()
Отже, ![]() і
і 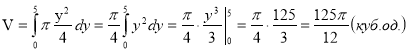
Відповідь: ![]()
Приклад 3. Знайти об’єм тіл, які утворені обертанням відрізка параболи
у = х2, ![]() навколо осі Ох і Оу.
навколо осі Ох і Оу.
Розв’язання
1. Об’єм тіла обертання відносно осі Ох розраховуємо за формулою:
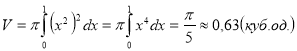
2. Для знаходження об’єму тіла обертання відносно осі Оу залежність ![]() замінюємо на залежність
замінюємо на залежність ![]() де
де ![]()
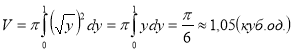
Відповідь: ![]()
![]()
3.3. ІІІ група Застосування визначеного інтеграла у фізиці.
А = 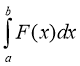 Роботу при прямолінійному русі
Роботу при прямолінійному русі
А = 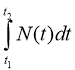 Робота при змінній потужності
Робота при змінній потужності
х =  Координата тіла
Координата тіла
v =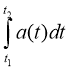 Швидкість тіла
Швидкість тіла
т = 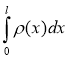 Маса стержня
Маса стержня
q (t) = 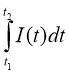 Заряд
Заряд
Q = 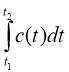 Кількість теплоти
Кількість теплоти
Приклад 1. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом v = 2t + 1 (м/с). Знайти шлях, який пройшло тіло за інтервал часу від t1 = 1 с до t2 = 3 с.
Розв’язання
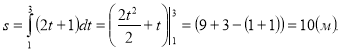
Відповідь: s = 10 м.
Приклад 2. Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний переріз зі стороною 2 м. Густина води ρ = 103 кг/м3.
Розв’язання
Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м2, визначається вагою шару води, що знаходиться вище від цього перерізу. Отже,
![]() де
де ![]()
![]() м/с.
м/с.
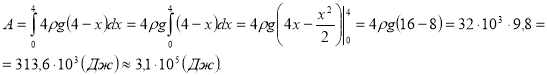
Відповідь: А = 3,1 · 105 Дж.
Приклад 3. Знати масу стержня завдовжки 35 см, якщо його лінійна густина змінюється за законом ![]()
Розв’язання
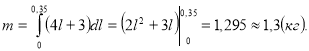
Відповідь: m = 1,3 кг.
Приклад 4. Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом ![]()
Розв’язання
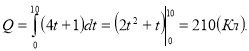
Відповідь: Q = 210 Кл.
3.4. ІV група Застосування визначеного інтеграла в економіці.
Попит на даний товар – залежність між ціною товару і об’ємом його покупки, що склалася на певний момент часу. Попит на окремий товар графічно зображується у вигляді кривої з від’ємним нахилом, що відображає взаємозв’язок між ціною Р одиниці цього товару і кількістю товару Q, яку споживачі готові купити при кожній заданій ціні. Від’ємний нахил кривої попиту має очевидне пояснення: чим дорожчий товар, тим менша кількість товару, яку покупці готові купити, і навпаки.
Аналогічно визначається і інше ключове поняття економічної теорії – пропозиція товару: залежність між ціною і кількістю запропонованого для продажу товару, що склалася на певний момент часу. Пропозиція окремого товару зображується графічно у вигляді кривої з позитивним нахилом, що відображає взаємозв’язок між ціною одиниці цього товару Р і кількістю товару Q, яку споживачі готові продати при кожній ціні.
І нарешті, введемо ще одне поняття, що відіграє велику роль в моделюванні економічних процесів – ринкову рівновагу. Стан рівноваги характеризують такі ціна і кількість товару, при яких об’єм попиту співпадає з величиною пропозиції, а графічно ринкова рівновага зображується точкою перетину кривих попиту і пропозиції.
Споживацький надлишок – явище в економіці, яке викликане перевищенням пропозиції даного товару над його попитом. Споживацький надлишок можна розрахувати за наступною формулою: 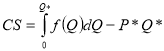
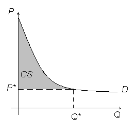
Якщо f(t) – продуктивність праці в момент t, то ![]() =
=![]() – обсяг продукції, яка випускається за проміжок часу [0; T].
– обсяг продукції, яка випускається за проміжок часу [0; T].
Приклад1. Продуктивність праці робітника протягом дня задається функцією z(t) = – 0,00645t2 + 0,05t + 0,5 (грош. од./год), де t – час в годинах від початку роботи, 0 ≤ t ≤ 8. Знайти функцію ![]() яка показує обсяг продукції (у вартісному виразі) та його величину за робочий день.
яка показує обсяг продукції (у вартісному виразі) та його величину за робочий день.
Розв’язання:
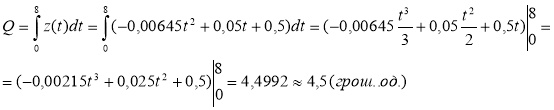
Відповідь: 4,5 грош. од.
Нехай відома функція t = t(х), яка описує зміни витрат часу t на виготовлення виробів в залежності від степеня засвоєння виробництва, де х – порядковий номер виробу в партії. Тоді середній час tсер, затрачений на виготовлення одного виробу в період засвоєння від х1 до х2 виробів, обчислюється за теоремою про середнє значення: tсер=![]()
![]() .
.
Приклад2. Знайти середній час, затрачений на засвоєння одного виробу в період засвоєння від х1=100 до х2=121 виробів, вважаючи в формулі t = ах-b, що а=600 хв., b=0,5.
Розв’язання: Використовуючи формулу середнього часу, отримуємо
tсер=![]()
![]() =
=![]()
![]() =
=![]() 2
2![]()
![]() =
= ![]()
![]() 57,2 (хв).
57,2 (хв).
Відповідь. 57,2 хв.
Якщо кількість товару, що надходить на склад в одиницю часу позначити через f(х), де х – час, який відлічується від початку надходження товару на склад, то від початку прийому на складі утвориться запас товару
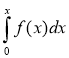 . Якщо навантаження на електростанцію задається функцією f(х) (в кВт·год, де х – кількість годин, яка відлічується від початку доби), то витрати електроенергії протягом доби складають
. Якщо навантаження на електростанцію задається функцією f(х) (в кВт·год, де х – кількість годин, яка відлічується від початку доби), то витрати електроенергії протягом доби складають 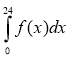 , а протягом часу х витрати електроенергії складуть
, а протягом часу х витрати електроенергії складуть 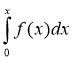 .
.
4.Закріплення вивченого матеріалу (метод корекції знань, формування навичок, предметних компетенцій, розв’язування задач)
А зараз, панове, давайте перенесемося в майбутнє, років на 20 вперед. Ви – дорослі, солідні люди, знайшли своє місце в житті: конструктори, інженери, металурги, будівельники, економісти, плановики, вчені. І в процесі своєї роботи ви зустрічаєтеся з різними проблемами, які вам необхідно вирішити.
Кожна підгрупа отримує певне завдання і звітує про виконану роботу.
Фінансисти
На полі пшениці після приземлення космічного корабля залишився слід, який нагадує фігуру, обмежену лініями у = - ( х- 1)2 + 9 та у = х+2. Необхідно визначити збитки, завдані агрокомплексу, якщо з 1 м2 отримують в середньому 3,8 кг пшениці, яка коштує 0,8 грн. / кг.
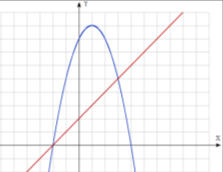
Розв’язання:
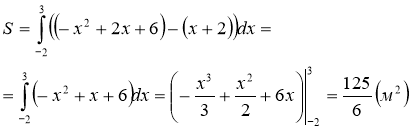
Маса пшениці: ![]()
Ціна: ![]()
Відповідь: 63, 34 грн.
Археологи
Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = – х2 + 4 навколо осі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м3. Яку масу каменю використали на виготовлення цього жертовника стародавні майстри?
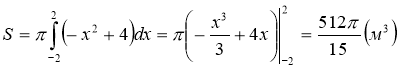
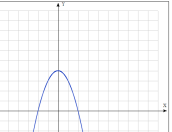
![]()
Відповідь: 85333, 33 кг.
Фізики
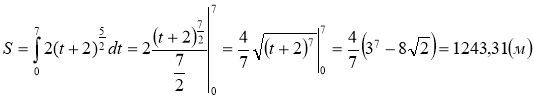 Для кращого обслуговування заїзду гонок серії „Формула-1” майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 2·(t+2)5/2. Який шлях проїде пілот цієї гонки за 7 с від початку руху?
Для кращого обслуговування заїзду гонок серії „Формула-1” майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 2·(t+2)5/2. Який шлях проїде пілот цієї гонки за 7 с від початку руху?
Відповідь: 1243,31 м
Енергетики
Навантаження на теплоелектростанцію задається функцією f(x) = 3x2 + 4x – 2. Визначити витрати електроенергії протягом доби.
Розв’язання:
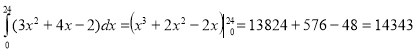 ( кВт·год)
( кВт·год)
Відповідь: 14343 кВт·год.
Математика – потужна зброя в руках фізика, економіста. Адже багато наслідків можна одержати математично, використовуючи перевірені дослідом формули. Зараз ви покажете, як використовуючи цю зброю, ви виконали своє завдання.
5. Узагальнення та систематизація знань студентів. (метод: виконання тестових завдань )
Розв’язування тестових завдань „Перевір себе”
1. За якою з наведених формул визначається площа даної фігури?
![]()
![]()
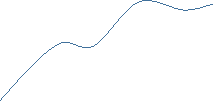
![]() у 1. S =
у 1. S = 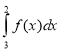 .
.
f(x) 2. S = ![]() .
.
![]() 1 2 3 x 3. S =
1 2 3 x 3. S = ![]() +
+ 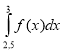 .
.
4. S = – 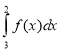 .
.
2. Знайдіть в яких записах є помилка.
1. 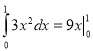 2.
2. 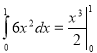
3. 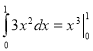 4.
4. 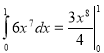 .
.
3. За якою з наведених формул обчислюється робота змінної сили, заданої формулою F(x)= 3x2–4x+8, вздовж відрізка довжиною 2 м?
1. А=![]() 2. А=
2. А=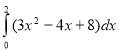 .
.
3. А=(3х2-4х+8)΄. 4. А=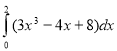 .
.
4. За якою з формул обчислюється обсяг виготовленої за 4 години продукції, якщо продуктивність праці задається формулою f(x)= 4x3?
1. ![]() . 2.
. 2. 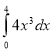 . 3. (4х3)΄. 4.
. 3. (4х3)΄. 4. 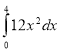 .
.
5. В якому випадку вірно обчислено навантаження електростанції за 3 години, якщо її витрати визначаються функцією f(x) = ![]() ?
?
1. 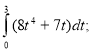 2.
2. 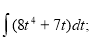
3. 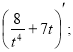 4.
4. 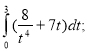
6. Підсумки заняття.
Скажіть, будь ласка, що саме ми з вами робили сьогодні на занятті?
(розв’язували задачі з геометрії, фізики, економіки, перекладали мовою математики проблеми, які стоять перед іншими науками.)
На сьогоднішньому занятті ми ще раз переконалися в тому, що математичні теорії є надійним знаряддям в розкритті таємниць природи, законів економічних процесів.
7. Домашнє завдання. Конспект лекції, тренувальні вправи.
1. Обчислити площу фігури, обмеженої: кубічною параболою у = х3, віссю Ох та прямими х = 2 і х = 5.
Розв’язання
![]()
2. Матеріальна точка рухається прямолінійно зі швидкістю v(t) = 5,5 – t. Знайдіть шлях, який пройшла точка за перші 8 с руху.
3. Визначити середній час, витрачений на засвоєння одного виробу від 10 до 20 виробів, якщо функція t = 3х описує зміни витрат часу t на виготовлення виробів в залежності від степеня засвоєння виробництва.
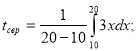
Ми зійшли на вершину гори, долаючи труднощі, виявляючи нетерпіння, наполегливість. На шляху нам зустрічалися явища, для розуміння і пояснення яких необхідні математичні знання. Прочитайте фразу, написану на плакаті: „Забути не можна пам’ятати!”
Від того, у якому місці ви поставите кому, матимете два варіанти: „Забути, не можна пам’ятати!” або „Забути не можна, пам’ятати!”
На якому варіанті ви зупинитесь? Чи потрібні вам знання з математики в майбутньому?
Рецензія
Методична розробка заняття відповідає всім методичним вимогам проведення занять виду інтерактивної лекції і складена у повній відповідності до програми з дисципліни ”Вища математика ”. В розробці відображено всі етапи заняття.
Викладка матеріалу проводиться послідовно на належному науковому рівні із застосуванням інформаційно – комунікативних технологій. Кожен інформаційний модуль закріплюється в процесі заняття за допомогою влучних прикладів, конкретних вправ по темі. Матеріал теми перекликається з темами з дисципліни «Математика» та базується на матеріалі вивченому на попередніх заняттях , тому студенти мають можливість взяти участь у з’ясуванні деяких властивостей та теоретичних фактів.
В методичні розробці висвітлено багато різноманітних форм та методів роботи: навчальний тренінг, інструктування, самостійна робота, тренувальні вправи, бесіда, ілюстрація, пояснення, тощо.
Методична розробка забезпечена всіма необхідними матеріалами візуального супроводження, роздатковими матеріалами. Підготовлено презентацію заняття для мультимедійного проектора.
Студенти виступають активними учасниками навчального процесу, виробляють свій власний погляд на інформацію, намічають мету й задачі й шукають шляхи їх вирішення.
Дана методична розробка може бути використана для проведення заняття з дисципліни «Вища математика» по темі «Визначений інтеграл».
Рецензент / Кордонська І.В. /
1


про публікацію авторської розробки
Додати розробку