Заняття з вищої математики. Тема " Розв'язування систем лінійних алгебраїчних рівнянь"

Новокаховський політехнічний коледж

 Одеського національного політехнічного  університету

 Викладач математики  Опята Л.І.

 

ЗАНЯТТЯ  З  ВИЩОЇ  МАТЕМАТИКИ

 

ТЕМА: Розв’язування  систем  лінійних  рівнянь  засобами Excel

 

МЕТА: Познайомити  учнів з методами  розв’язування систем  лінійних  рівнянь  засобами  Microsoft Excel, розвивати увагу, розвивати алгоритмічне мислення, працювати над формуванням математичної культури та мови учнів, формування навиків роботи засобами Excel.

Тип заняття. Заняття засвоєння  нових  знань. 

Обладнання: Заняття  проводиться в  комп’ютерній аудиторії, проектор, роздатковий і дидактичний матеріал до заняття.

Девіз заняття:

 

1.Природа формує свої закони  мовою математики (Галілео Галілей).

 

2.Сухие строки уравнений ! В них сила разума влилась.

   В них – объяснение явлений, вещей разгаданная страсть.

 

Хід  заняття.

1. Мотивація.

Повідомляємо тему та мету заняття.

2. Вступне слово  викладача.  

Поведінка великої кількості об’єктів зовнішнього світу задовільно описується системою лінійних алгебраїчних рівнянь. Досить широкий клас математичних моделей об’єктів, які описуються лінійними рівняннями належить до задач економіки. До таких задач слід віднести, наприклад,  транспортні задачі, та задачі планування виробництва, завантаження верстатів, рівноваги системи важелів або пружин тощо. Без рівнянь немає математики як засобу пізнання природи.

3. Актуалізація   опорних  знань.

Фронтальне  опитування: (технологія «мікрофон»)

1)Які  методи розв’язування систем лінійних рівнянь  ви знаєте?

2)Яка  система рівнянь називається  сумісною?

3)Що називається розв’язком системи лінійних рівнянь?

4)Які системи рівнянь називаються рівносильними, та як вони можуть отримуватись?

5)Сформулюйте теорему Крамера.

6)В чому заключається суть матричного методу?

7)В чому полягає метод Гаусса?

8)Які функції, що вбудовані в пакет Microsoft Excel,  застосовуються до дій з матрицями?

     4. Формування навичок розв’язування систем  лінійних  рівнянь  засобами  Excel.

4.1Розв’яжемо систему лінійних алгебраїчних рівнянь:

     

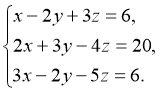
Застосуємо метод Крамера. Для цього знайдемо визначник , та _х ,_у ,_z .

Для виконання такої операції в Excel існує функція МDETERM(масив).

Алгоритм:

1.Визначник заносимо в інтервал комірок. Наприклад А1:С3, що складається з трьох рядків і трьох стовпців.

2.Табличний курсор поставте в комірку в якій потрібно отримати значення визначника, наприклад в F2.

3.Натисніть на панелі інструментів кнопку «вставка функції»

4.В діалоговому вікні «Мастер функції» в робочому полі «Категорія» вибираємо «Математичні», а в робочому полі функція – ім’я функції МDETERM. Після цього натисніть кнопку «ОК».

5.В діалоговому вікні що з’явилось введіть діапазон матриці А1:С3 в робоче поле «Масив». Натисніть кнопку «ОК».

6.В комірці F2 з’явиться значення визначника матриці    .

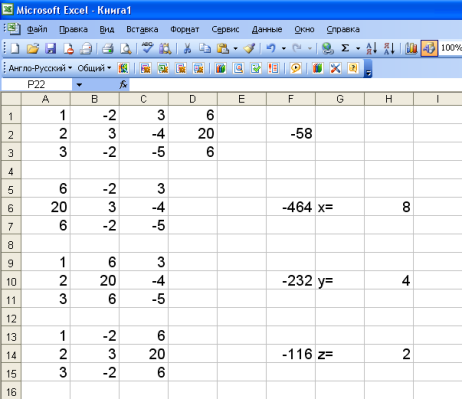
Аналогічно обчислюємо  _х ,_у ,_z . (Див. рисунок)

 

 

4.2. Розв’яжемо задану систему рівнянь матричним методом. Для цього систему запишемо у вигляді матричного рівняння АхХ=В, де А – матриця коефіцієнтів при змінних, Х – матриця -  стовпець при невідомих, В – матриця стовпець вільних членів. Розв’язком системи методом оберненої матриці буде матриця – стовпець Х=А^-1 х В. Таким чином, для розвязування системи необхідно знайти обернену матрицю коефіцієнтів і помножити її справа на вектор вільних членів. Розглянемо ці операції в пакеті Excel.

Розв’язування :

1.Введемо матрицю А в діапазон А2:С4, а стовпець вільних членів в діапазон D2:D4.

2.Знайдемо обернену матрицю А^-1 . Для цього:

- виділяємо блок комірок під обернену матрицю. Наприклад А7:С9.

- натисніть на панелі інструментів кнопку «вставка функції»

- в діалоговому вікні «Мастер функции» в робочому полі «Категорія» вибираємо «Математичні», а в робочому полі функція – ім’я функції МINVERS. Після цього натисніть кнопку «ОК».

- в діалоговому вікні що з’явилось введіть діапазон матриці А2:С4 в робоче поле «Масив». Натисніть комбінацію клавіш «CTRL+SHIFT+ENTER»

- якщо обернена матриця не з’явилася в заданому діапазоні, то необхідно клацнути «мишкою» в рядку формул і повторити комбінацію клавіш  «CTRL+SHIFT+ENTER».

Розв’язування має  вигляд (див.рис.)

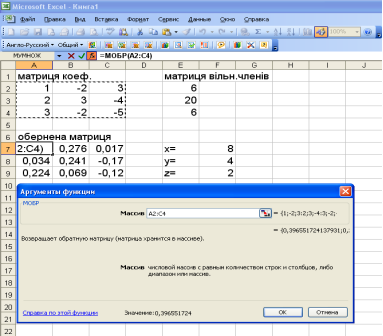
3.Множенням оберненої матриці А^-1 на матрицю В знайдемо матрицю Х. Для цього:

- виділимо блок комірок під результативну матрицю (під матрицю Х). Наприклад

- натисніть на панелі інструментів кнопку «вставка функции»

- в діалоговому вікні «Мастер функции» в робочому полі «Категорія» вибираємо «Математичні», а в робочому полі функція – ім’я функції МMULT. Після цього натисніть кнопку «ОК».

- в діалоговому вікні що з’явилось введіть діапазон оберненої матриці A7:C9 в робоче поле «Масив 1», а матриці В робоче поле «Масив 2». Натисніть комбінацію клавіш «CTRL+SHIFT+ENTER»

- якщо матриця Х не з’явилася в заданому діапазоні, то необхідно клацнути «мишкою» в рядку формул і повторити комбінацію клавіш  «CTRL+SHIFT+ENTER».

 

 

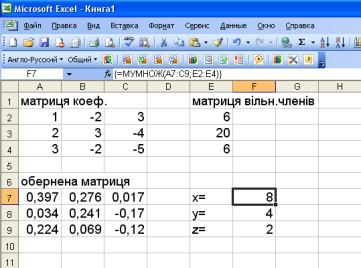
Можна виконати перевірку знайденого розв’язку.

4.3Розв’яжемо систему лінійних алгебраїчних рівнянь:

                                              

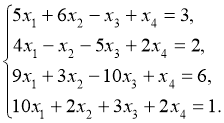
Розв’язування заключається у множенні оберненої матриці коефіцієнтів при невідомих на матрицю вільних членів. Ці операції можна виконувати послідовно, тобто спочатку визначити обернену матрицю коефіцієнтів при невідомих      за допомогою функції МINVERS, а потім отриману обернену матрицю помножити на матрицю вільних членів за допомогою функції МMULT. Але все це можна виконати скоріше: спочатку викликається функція МMULT, в діалоговому вікні якої викликається вбудована функція у першого масиву, де в свою чергу викликається функція обернення та вводиться матриця коефіцієнтів. Для другого масиву діалогового вікна функції МMULT вводиться діапазон матриці вільних членів. Введення закінчується комбінацією клавіш «CTRL+SHIFT+ENTER». Наприклад, якщо матриця коефіцієнтів записана в діапазоні А2:D5, а матриця вільних членів в діапазоні G2:G5, то формула має вигляд:

Розв’язування системи рівнянь має вигляд:  

 

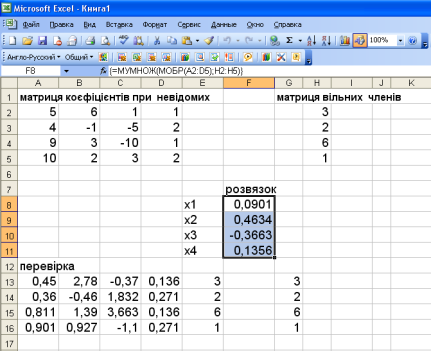
4.4 При прогнозах і оцінках функціонування підприємств, планування мікроекономіки підприємств використовуються задачі такого типу.

Задача 1: Підприємство випускає три види продукції використовуючи при цьому три види сировини. Характеристики виробництва задані таблицею:

 

Вид сировини	Витрати сировини за видами, на од.прод.			Запаси сировини
	A	B	C
1 2 3	6 4 5	4 3 2	5 1 3	2400 1450 1550

 

Визначити план випуску продукції кожного виду використавши всі запаси.

Розв’язання. Нехай х₁ , х₂ , х₃ – невідомі, поки що, об’єми випуску продукції. При умові повного використання запасів, можна забезпечити балансові співвідношення, які задовольняють систему рівнянь :

        

                              

 

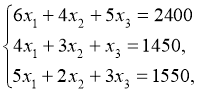
Самостійно розв’язуємо  систему  рівнянь. Розв’язок може  мати  вигляд: 

 

 

 

4.4Задача 2. Розглянемо спрощену модель фінансової математики, яку умовно називають «портфельними інвестиціями».

У реальному житті одним із багатьох джерел фінансування є міжнародні інвестиції. Країна може одержувати й надавати міжна­родні займи, приймати та інвестувати за кордон капітал. Продаж ак­тивів у будь-якій формі (права власності, цінні папери, золото тощо) означає приплив капіталу в країну. Серед інвестицій є портфельні — вкладення капіталу в іноземні цінні папери, які не дають інвестору права реального контролю над об'єктом інвестування. Такі інвестиції базуються переважно на приватному капіталі.

Припустимо, що інвестори можуть вкладати гроші в активи: в об­лігації (які дають точний фіксований прибуток), акції (які дають при­буток, що може змінюватися), в землю. Нехай після виборів у даній країні до влади може прийти одна з двох політичних партій Х₁ або Х₂. Зрозуміло, що доход від капіталовкладень залежатиме від державного устрою країни. Так, уряд партії Х₁ може збільшити ціну на землю й зменшити ціну акцій, а уряд партії Х₂ — навпаки. Наприклад, маємо таблицю:

 

Активи	Партія Х1	Партія Х2
Земля Облігації Акції	1,25 1,05 0,90	0,95 1,05 1,15

Дану таблицю можна записати як матрицю R = (r_ij), і = 1, 2, 3; j - 1,2 розміру 3x2, що визначає доход від кожного активу:  

Нехай інвестори вирішили вкласти $50 000 у землю, $100 000 — в облігації і $40 000 — в акції. Тоді дістанемо матрицю - рядок розміру 1 х 3: Р = (50 000 100000 40 000), яка характеризує портфельні інвестиції.

Добутком матриць PR буде матриця розміру 1 х 2, яка характеризує можливі вартості портфельних інвестицій, якщо на виборах переможе партія X₁ чи Х₂Отже,

 

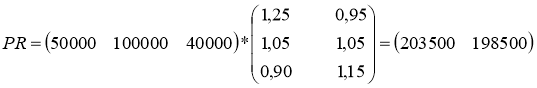
Можна зробити висновок: якщо на виборах переможе партія Х₁ , то вартість портфеля становитиме $203500, а якщо партія Х₂  то $1985000.

 

5.Підсумок  заняття.

5.1Фронтальне опитування.

5.2.Оцінювання.

6.Домашне завдання(практична  робота)