Тема уроку:

Застосування похідної до розв’язування задач прикладного   змісту

Мета уроку:

ознайомитися з різними типами прикладних задач та методами їх розв’язування за допомогою похідної; поглибити знання про моделювання процесів дійсності за допомогою апарата похідної; розвивати пізнавальний інтерес, навички колективної праці; виховувати організованість, працьовитість, увагу, інтерес до наук через звернення до історичних джерел.

Тип уроку: узагальнення та систематизація знань, умінь, навичок.

Наочність та обладнання: комп’ютер, проектор, інтерактивна дошка, презентація.

                                     Хід уроку

Ι. Перевірка домашнього завдання

Перевіряємо наявність домашньої роботи та правильність виконання, називавши відповіді до завдань.

ΙΙ. Актуалізація опорних знань

1.Знайти похідну функції   f(x) = 2х³ + 3х²

2.Знайти похідну функції  f(x) = 3х⁴ – 2х² +1

3.Знайти похідну функції  f(x) = + х²⁰ - 4

4.Знайти похідн у функції  f(x) = 2 + 4х³ +7

5.Повторення похідних функцій, правил обчислення похідних, рівняння дотичної до графіка функції в точці х₀:

Похідні функцій хⁿ,  , ,,   ,,   ctgх.

Похідна суми, добутку, частки, похідна складеної функції.

ЙЙЙ. Повідомлення теми і мети (слайди №1, 2).

ΙV. Сприйняття і засвоєння нових знань ( слайд №3).

     Похідна – одне з фундаментальних понять математики. Похідна характеризує швидкість зміни функції. Похідна та диференційованість функції.  Неперервність функції.    У 1670 -  1671 роках англійський математик і механік Ісаак Ньютон (1643 – 1727) і дещо пізніше (1673 – 1675) німецький філософ і математик Готфрід Вільгельм Лейбніц (1646 – 1716)незалежно один від одного побудували теорію диференціального числення.  

Нагадати фізичний і геометричний зміст похідної. Виступи учнів з історичною інформацією.       (Слайди №4, 5).    

           1.  Ньютон і диференціальне числення

       Диференціальне числення — розділ математики, в якому вивчаються похідні, диференціали та їх застосування в дослідженні властивостей функцій. Формування диференціального числення пов'язано з іменами Ісаака Ньютона та Ґотфріда Лейбніца. Саме вони чітко сформували основні положення та вказали на взаємообернений характер диференціювання та інтегрування. Створення диференціального числення відкрило нову епоху у розвитку математики. Методи математичного аналізу знайшли використання у всіх розділах математики. Дуже поширилася область застосування математики у природничих науках та техніці.

       Серед геніїв 17 ст. Ньютон і Лейбніц височать як недосяжні вершини. З ними пов’язано завершення формування математичної теорії, яка зумовила небачені раніше зрушення в історії математики і дала необмежені можливості для математизації теоретичного знання і практичної діяльності людини.

       Ньютон справді вмів захоплюватися обчисленнями і, забувши про все, думати над поставленими задачами, доки не бачив виходу з логічного лабіринту.  У галузі математики він завершив героїчний марафон пошуку і вдосконалення методів розв’язування знаменитих задач обчислення площ криволінійних фігур і проведення дотичних до кривих ліній у заданій точці.

       Для розв’язання задач фізики і астрономії потрібно було знати геометричні властивості фігур: механікам потрібні були алгоритми обчислення площ і центра ваги фігур, астрономам – об’ємів тіл обертання.

        Аналіз найважливіших задач природознавства виявив, що всі вони зводяться до відшукання дотичної за заданою кривою. Ньютон розв’язав їх у механічній формі, досліджуючи змінні біжучі величини, які назвав флюентами ( функціями) у взаємозв’язку зі швидкостями змін флюент – флюксіями (похідними). Усі флюенти Ньютона залежали від одного аргументу – часу t. Відшукання флюксії, коли задано флюенту – основна задача диференціального числення, тобто обчислення похідної даної функції.

        Ньютон на 10 років раніше за Лейбніца прийшов до відкриттів з математичного аналізу, Лейбніц на 28 років раніше за Ньютона опублікував свої результати. Вони починали незнайомцями, мали стати друзями, а завершили шлях ворогами.

 

 

           2. Лейбніц і диференціальне числення

         Диференціальне числення дає апарат для дослідження функцій, поведінка яких у досить малому околі кожної точки близька до поведінки лінійної функції чи многочлена. Таким апаратом слугують центральні поняття диференціального числення: похідна і диференціал. 

         У 1675 році Лейбніц створює диференціальне й інтегральне числення і згодом опубліковує головні результати свого відкриття, випередивши Ньютона, який ще раніше прийшов до схожих результатів і писав про них Лейбніцу у приватній переписці .

В 1684 році Лейбніц публікує першу у світі велику роботу по диференціальному численню: «Новий метод максимумів і мінімумів», причому ім'я Ньютона в першій частині навіть не згадується, а в другій заслуги Ньютона описані не цілком ясно.

        Тоді Ньютон не звернув на це уваги. Його роботи

з аналізу почали видаватися тільки з 1704 року. Згодом через це виникла багаторічна суперечка між Ньютоном і Лейбніцем про пріоритет відкриття диференціального числення. Ньютон написав два листа до Лейбніца, в яких повідомив про свої дослідження з аналізу, але без викладання методів. У відповідь Лейбніц описав деякі зі своїх методів, щодо яких Ньютон зневажливо зауважив: «…не розв'язане жодне попередньо відкрите питання…».      

         Ньютон виходив в основному із задач механіки, а Лейбніц – переважно з геометричних задач. Зокрема, до означення похідної Ньютон прийшов, розв’язуючи задачу про миттєву швидкість, а Лейбніц – геометричну задачу про проведення дотичної до кривої.

        Лейбніц виклав свої дослідження з математичного аналізу у декількох мемуарах, починаючи з «Нового методу для максимумів і мінімумів, а також дотичних», надруковані  в 1684 р. Зокрема, вже перший мемуар містить  правила для диференціювання добутків, часток і степенів, оскільки жодні з результатів методу флюксій Ісаака Ньютона, який він розробляв принаймні з 1671 р., ще не було надруковано. Вони з'явились лише у 1687 р.   

        Ці публікації Лейбніца згодом призвели до надзвичайно лютої і тривалої суперечки щодо пріоритету у створенні диференціального та інтегрального числення. Так чи інакше, ідеї Лейбніца та його нотація мали набагато більший вплив на розвиток математичного аналізу протягом наступного століття, особливо на континенті.

 

Вчені, які досліджували поняття похідної. (Слайд №6)

Де і як можна використовувати знання про похідну?   (Слайд №7)         

 Учні дають відповідь.          

V.  Набуття умінь та навичок розв’язування прикладних задач.

         1.  П о х і д н а  у  ф і з и ц і                 (Слайд №8).                      

         Тіло масою m₀    рухається   прямолінійно  за  законом

S(t) =   .      Довести, що сила, яка діє на тіло,   пропорційна кубу пройденого шляху.                                                     

         2. П о х і д н а  в  е л е к т р и ц і       (Слайд №9).

         Нехай  в момент  часу t через поперечний переріз провідника         проходить кількість електрики          q  =   .

Знайти силу струму в момент часу t = 2 с.

 

3. П о х і д н а  у  п о б у т і            (Слайд №10).

 

         Нехай маємо квадратний лист заліза із стороною a. Треба в кожному куті його відрізати такі квадрати, щоб після згинання країв отримати ящик найбільшої місткості.

4. З а в д а н н я  з  ЗНО                 (Слайд №11).

 

        Обчисліть f ‘(1), якщо кут між дотичною, проведеної до графіка функції  y = f(x)   у точці з абсцисою   x₀ = 1    і  додатнім напрямом осі OX,  дорівнює   30°  .

5. П о х і д н а  у  г е о м е т р і ї     (Слайд №12).

      у

                                              

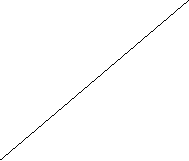
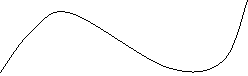
                                                                                 На малюнку зображений графік  функції у = f(x)   та дотичні до нього

                                                                       в точках   x₁  та  х₂.  

 х₁             45                 х₂                   х

                                                         Користуючись геометричним змістом

                                           похідної,  знайдіть   f ‘(x₁) + f ‘(x₂).

      6. Р і в н я н н я  д о т и ч н о ї   в точці х = х₀   (Слайд №13) .

       Знайдіть, при яких значеннях  параметра  а  дотична до графіка функції   у = х³ + ах²    у точці з абсцисою    х₀  = -1           проходить через точку  N(3;4).

      7.П а р а л е л ь н і с т ь  п р я м и х                     (Слайд №14)

      На параболі  y =  4 – х²    вибрано дві точки  з   абсцисами x= -1    і     x=3.      Через ці точки   проведено січну.     Знайти рівняння    дотичної  до параболи,  яка паралельна січній.

VΙ. Самостійне опрацювання тестів.

                                              

 

  Ι варіант

1. Знайти  кут, який утворює з додатним напрямом осі  х  дотична до графіка функції    у = х⁴    у  точці  х₀ = -1.

 

А	Б	В	Г	Д
30°	45°	120°	135°	150°

 

2. Рівняння дотичної  до кривої   у = 2х² – 4х – 1  має вигляд:   у = 8х – 19.  Визначити  абсцису точки дотику.

 

А	Б	В	Г	Д
2	3	4	-4	8

 

3. На кривій  f(x) = х² – х + 1  знайти точку, в якій дотична до кривої паралельна до прямої  у = 3х – 1.

А	Б	В	Г	Д
(2; 3)	(0; 3)	(0; 1)	2	3

 

4. Матеріальна точка рухається прямолінійно за законом  s(t) = 2,5t² – 15t,

 s – шлях  у метрах, t – час у секундах. Через який час від початку руху ця точка зупинилася?

А	Б	В	Г	Д
1с	2с	3с	3,5с	4с

 

5. Знайти критичні точки функції   f(x) = - х² – 3х.

 

А	Б	В	Г	Д
0	-3 і -1	-3 і 1	1 і 3	-1 і 3

 

6. Визначити проміжок зростання функції  у = х² – 1.

А	Б	В	Г	Д
(-	[0;	[1;	(- -1)	(-

 

7. Установити  відповідність між функціями  (1 – 4) та їхніми похідними  (А – Д).

 

1. у = + 5                                                                   А  у' = -3

                                                                                                         Б   у' = 5

2. у = 5 -                                                                      В  у' = -

 

3. у = 3 + 5х                                                                   Г  у' = -5

 

4. у = 5 – 3х                                                                   Д  у' =

 

8. Установити відповідність між залежностями відстані S від часу t руху матеріальних тіл  (1 – 4)  та їх швидкостями в момент часу  t = 1  (А – Д).

 

1. S(t) =8 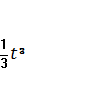+ 5t                                                          A   4

                                                                                    Б   5

2. S(t) = 4t + 1                                                                В  5

 

3. S(t) = + 5t                                                              Г  5

 

4. S(t) =2t² + t                                                                 Д  30

 

 

                               ΙΙ варіант

 

1.Знайти  кут, який утворює з додатним напрямом осі  х  дотична до графіка функції    у = х³    у  точці  х₀ = 1.

А	Б	В	Г	Д
30°	45°	120°	135°	150°

 

  2.Рівняння дотичної  до кривої   у = 3х² – 2х + 1  має вигляд:   у = 4х  + 9.       Визначити  абсцису точки дотику.

А	Б	В	Г	Д
2	3	4	-4	1

 

3.На кривій  f(x) = х² + х - 2  знайти точку, в якій дотична до кривої паралельна   до   прямої  у = 3х + 1.    

А	Б	В	Г	Д
(2; 3)	(0; 3)	(1; 0)	2	3

 

  4. Матеріальна точка рухається прямолінійно за законом  s(t) = 1,5t² – 9t,  s – шлях  у метрах, t – час у секундах. Через який час від початку руху ця точка зупинилася?

А	Б	В	Г	Д
1с	2с	3с	3,5с	4с

 

5.Знайти критичні точки функції   f(x) = - 2х² + 3х.

А	Б	В	Г	Д
0	-3 і -1	-3 і 1	1 і 3	-1 і 3

 

   6.Визначити проміжок спадання функції  у = х² – 1.

 

А	Б	В	Г	Д
(-	[0;	[1;	(- -1)	(-

 

7. Установити  відповідність між функціями  (1 – 4) та їхніми похідними  (А – Д).

 

1. у = + 5                                                                   А  у' = 5

                                                                                                 Б   у' = -3

2. у = 5 -                                                                      В  у' = -

 

3. у = 3 + 5х                                                                   Г  у' = -5

 

4. у = 5 – 3х                                                                   Д  у' =

 

8. Установити відповідність між залежностями відстані S від часу t руху матеріальних тіл  (1 – 4)  та їх швидкостями в момент часу  t = 1  (А – Д).

 

1. S(t) =8 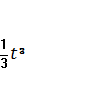+ 5t                                                       A   5                                                                                                                                                                         

                                                                                 Б  30

2. S(t) = 4t + 1                                                             В  5

 

3. S(t) = + 5t                                                            Г  5

 

4. S(t) =2t² + t                                                               Д  4

VΙΙ. Підсумок уроку.

VΙΙΙ. Домашнє завдання.