Довідковий матеріал до теми "Елементи комбінаторики"

А Л Г Е Б Р А,  11            ТЕМА 6.  ЕЛЕМЕНТИ  КОМБІНАТОРИКИ,

                                    ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ І МАТЕМАТИЧНОЇ СТАТИСТИКИ

Комбінаторика – розділ математики, присвячений розв’язанню задач вибору і розташування елементів
                                      скінченної множини відповідно до заданих правил.

Операції  над  множинами

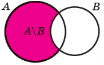
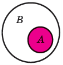
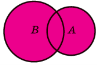
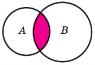
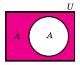
                A \ B                          А  В                        A  B                           A  B                        = U \ A

                                                                     Правило суми

Якщо елемент множини А можна вибрати m способами,
а елемент множини В – n способами,
то А або В можна вибрати m + n способами.

Правило добутку

Якщо елемент множини А можна вибрати m способами,
а після цього елемент множини В – n способами,
то А і В можна вибрати m  n способами.

     Приклад. Від селища А до селища В можна доїхати трьома дорогами, а від В до С – двома.

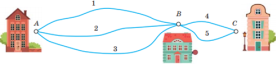
Скільки існує маршрутів, Скільки існує маршрутів,

щоб виїхати з селища В?                                                                                                                                 щоб дістатися від А до С?

Сполуки  без  повторень

Впорядкована множина -  скінченна множина з n елементів, кожному елементу якої поставлено у
                                                       відповідність будь-яке натуральне число від 1 до n (номер елемента).

    Перестановки                                     Розміщення                                            Комбінації

Будь-яка впорядкована                   Будь-яка n-елементна впорядкована                                    Будь-яка n-елементна

множина з m елементів            підмножина даної m-елементної множини            підмножина даної m-елементної множин

Приклад 1. У класі навчається 30 дітей. Скількома способами із цього класу можна вибрати …

                                                        …старосту і його заступника?                                               …двох чергових?

Розв’язання

                                  Обов’язки різні! Порядок має значення.            Обов’язки однакові! Порядок не має значення.

Відповідь. 870; 435.

                                   Приклад 2. Із вази з фруктами, в якій лежить 10 різних яблук і 5 різних груш, потрібно
                                                         вибрати 2 яблука і 3 груші. Скількома способами можна зробити такий вибір?

Розв’язання

Вибрати 2 яблука з 10 можна способами. При кожному виборі яблук груші можна вибрати способами. З За правилом добутку вибрати потрібні фрукти можна способами.
Таким чином,

Відповідь. 450.

                       Трикутник  Паскаля                                                        Біном  Ньютона

                     1                                                                                                        (a + b)⁰ = 1;

                  1   1                                                                                          (a + b)¹ = 1·a + 1·b;

               1   2   1                                                                             (a + b)² = 1·a² + 2ab + 1·b²;

             1   3   3   1                                                             (a + b)³ = 1·a³ + 3a²b + 3ab² + 1·b³;

         1   4    6   4   1                                               (a + b)⁴ = 1·a⁴ + 4a³b + 6a²b² + 4ab³ + 1·b⁴;

      1   5   10   10   5   1                            (a + b)⁵ = 1·a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + 1·b⁵;

   1 =            = 1                  = 1                  (a + b)^m = a^m +a^m-1b +…+ a^m-nbⁿ +…+ b^m.