Застосування похідної та інтеграла у природничо – математичних науках
Застосування похідної
та інтеграла у природничо –
математичних науках
Інтегрований урок , брейн - ринг ( з використанням групової роботи ).
Алгебра 11 клас
Вчитель математики Дунаївської ЗОШ І – ІІІ ступенів
Федак О.Я.
Тема уроку: Застосування похідної та інтеграла у природничо –математичних науках
Мета уроку: Показати зв'язок математичного аналізу з
природничими науками, поглибити зміст похідної і інтеграла.
Епіграф уроку: Природничі науки досягають тоді досконалості,
коли їм вдається користуватися математикою.
Тип уроку: Інтегрований урок , брейн - ринг ( з використанням
групової роботи ).
Хід уроку
Сьогодні наш урок проходить у дні святкування 200річчя з дня народження видатного поета, митця, пророка українського народу Т.Г. Шевченка, адже
у математиці є своя поезія, своя філософія. Вона дає людині силу мислення. Якщо відкрити тайни математики, тоді і природничі науки і фізика стануть для вас легкими. Це на все життя вас зробить сильними духом. Сьогоднішній урок не просто урок математичного аналізу, а урок зв’язку диференціального інтегрального числення з принципами механіки із законами фізики, економіки Отже у класі наш урок сьогодні інтегрований, це урок Брейн – ринг на кращу команду, яка продемонструє знання з алгебри і початків аналізу та фізики, має наступний план, який складається з 5 – геймів .(Гейм – вид завдання, форма роботи). Особливість цих завдань полягає в тому, що результати всіх відповідей певною мірою міститимуть деякі відомості про життя та творчість великого українського поета Т.Г. Шевченка.
Розминка
Учітеся, брати мої,
1) 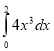 ; ( 16) 2)
; ( 16) 2) ![]() ; (180) думайте, читайте…
; (180) думайте, читайте…
3) 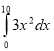 ; (1000)
; (1000)
4)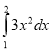 ; (5)
; (5)
1.План
1) «Первісна, похідна, інтеграл.»
2)«Фізичний етюд.»
3)«Похідна і закони фізики»
4)«Інтеграл у природничих науках.»
5)«Підведення підсумків»
І. Актуалізація опорних знань і умінь учнів.
1. Таблиця похідних.
2. Таблиця по формулах первісних.
ІІ. Знайди похідні функції (Завдання на дошці)
Скільки років було Т.Г. Шевченкові, коли вийшла його збірка поезій «Кобзар», яка поклала початок новому періоду в історії української літератури?
1. І команда ІІ команда ІІІ команда
y =5 y=-2 y=0.5
y=x2+4 y=4-2x6 y=![]() x3+7
x3+7
y=x![]() -2
-2![]()
![]() y=3x
y=3x![]() +1 y=4-2x
+1 y=4-2x![]()
y=cos x+26х y=2 sin x -5,5+26х y=3 tg x- 34+26х
2. Знайти первісні функцій у точці (ЗНАЧЕННЯ С)
Шевченко із 47 років життя …….. років був на засланні……..роки –був кріпаком і лише ……… років був на волі
М(-1;6) К(1;3) В(2;12)
1) y=4 (10р) y=-21 (24р) y=-0,5;(13р)
2) y= cos x y=sin x y=![]()
![]()
3) y=x y=2-x y=x-5
3. Знайти інтеграли.
![]()
![]()
![]()
![]()
![]()
![]()
ІІІ. Розв’язування задач із записом на дошці
(задачі в конвертах розв’язуються)
У цьому завданні кількість букв у назві відомого твору Т.Шевченка (3б. «Сон»)
1)Задача.
Знайти масу стержня завдовжки 1м, якщо його лінійна густина змінюється за законом
р(l)=(4l+1)(кг/м)
Розв`язання.
т=![]() =(2t2+l)
=(2t2+l)
=3кг
Відповідь:3кг
№2. Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лініями: у= 4х+1 х=1, х=2, у=0
Відповідь: 3м3
№3 Продуктивність праці: f (t) =2t -2; t- робочий час (у годинах).
Знайти обсяг продукції за третю годину робочого дня.
Відповідь: (3одиниці).
ІV. Завдання по темі застосування диференціального рівняння в біології, економіці.
1)Задача з розмноження мікроорганізмів.
У лабораторній посудині знаходяться К0 мікроорганізмів і є вдосталь поживних речовин для їх розмноження.
Знайти закон розмноження.
2)Задача з економіки
Дано:
Продуктивність праці: f (t) = -0,0033t -0,089t+20,96
- t- робочий час (у годинах)
- Тривалість робочого дня – 8 годин
- К-ть робочих днів – 22(на місяць)
Знайти
Обсяг продукції,випущеної потягом місяця.(презентація)
Яка з команд розв’яже швидше ( задачу )
Швидкість руху тіла змінюється за законом ![]()
![]() .Знайти шлях пройдений за 2год. від початкового руху.
.Знайти шлях пройдений за 2год. від початкового руху.
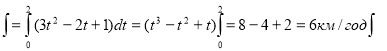 кількість букв у назві твору у якому співаємо пісню про дерево
кількість букв у назві твору у якому співаємо пісню про дерево
V. Відомості з історії виникнення диференціального числення.
Виступи, оцінення рефератів. Історичні довідки.
- Евдокс Кнідський (бл. 408-355 рр. до н. е.) - старогрецький вчений. Дав повний доказ теореми про обсяг піраміди; теореми про те, що площі двох кіл відносяться як квадрати їх радіусів. При доведенні він застосував так званий метод «вичерпання», який знайшов своє використання (з деякими змінами) у працях його послідовників. Через дві тисячі років метод «вичерпання» був перетворений у метод інтегрування, за допомогою якого вдалося об'єднати різні завдання - обчислення площі, об'єму, маси, роботи, тиску, електричного заряду, світлового потоку і багато, багато інших.
VІ. Підбиття підсумків.
Встановити відповідність між інтегралами та їх значеннями
Яка з фігур не є криволінійною трапецією
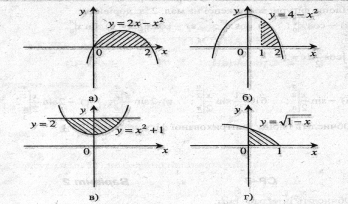 (в) (ЗА)
(в) (ЗА)
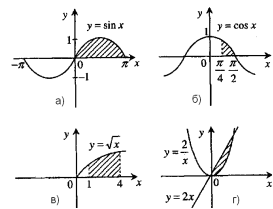
- Площа фігури, зображеної на мал. б), дорівнює:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() (а) (ПО)
(а) (ПО)
- Площа фігури, зображеної на мал. а), дорівнює:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() (а) (ВІТ)
(а) (ВІТ)
VІІ. Домашнє завдання №27.2(2), № 27.3 ст.273
Підсумок: Отже поет, музикант повинен бачити, відчувати те, чого не бачать інші, бачити глибше, відчувати тонше як і математик. Математика, як музика вона облагороджує людину, робить її душу ніжнішою не позбавляє її тонкого почуття.
Тож нехай диференціюється в наших душах зло, а інтегрується добро.
Теорема Піфагора
8 клас
урок узагальнення і систематизації знань учнів.
Вчитель математики Дунаївської ЗОШ І – ІІІ ступенів
Федак О.Я.
Тема уроку: Теорема Піфагора.
Мета уроку: Формування вміння самостійно розв’язувати
задачі на застосування теореми Піфагора і наслідків з неї. Розвивати увагу, логічне мислення, просторову уяву. Показати застосування набутих знань в практичній діяльності.
Епіграф уроку: «Світ, що нас оточує, це світ геометрії. Тож
давайте його пізнавати!»
Тип уроку: урок узагальнення і систематизації знань учнів.
Хід уроку
І. Організаційний момент.
І. Актуалізація опорних знань і умінь учнів.
На даному уроці ми підведемо підсумки основних знань по
вивченій темі.З метою повторення вивченого теоретичного матеріалу. Ви розгадаєте кросворд і знайдете ключове слово до основної теми.
1) В якому трикутнику сума двох кутів дорівнює першому.
2) В прямокутному трикутнику будь-який із катетів менший за……….?
3) Що означає запис ![]() ?
?
 4)
4)
![]() що означає
що означає ![]() для кута ?
для кута ?
5) Трикутник із сторонами: 3; 4; 5?
6) ![]() відносяться до кута є?
відносяться до кута є?
7) Синуси, косинуси, і тангенси яких кутів розглянемо?
1) Хто такий Піфагор?
2) Як читається теорема Піфагора?
3) Як знайти катет знаючи гіпотенузу і косинус прилеглого кута?
4) Як знайти катет знаючи гіпотенузу і синус протилежного кута?
5) Як знайти катет знаючи tq прилеглого кута і катет до кута.(учні записують на дошці)

![]()
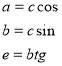
ІІ. Перевірка домашнього завдання ( фронтальна)
(оголошення теми і мети уроку)
Усний рахунок.
1)

![]()
2)
![]()
3)

![]()
4)
![]()
Чи може sin =1 cos =1 ?Чому?
ІІІ. Повідомлення теми і мети уроку.
Колективно:
В прямокутному трикутнику з кутом ![]() .Гіпотенуза дорівнює 10 см: Знайти
.Гіпотенуза дорівнює 10 см: Знайти ![]() трикутника.
трикутника.

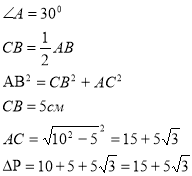
![]() Завдання самостійно по групах:
Завдання самостійно по групах:
І група
2) Відповіді: c=10, ![]() R=5
R=5
3) x=109.
ІІ група
1) Відповіді: ![]()
2) a=32; 60
3) NP =5 см; NQ=9 см; різниця 4см.
І. група
1) ![]()
2)![]()
![]()
3)Діагональ ![]()
ІІІ. Розв’язання цікавої задачі.
Задача індійського вченого Бхаскара.
(Задачі складались у віршовій формі, щоб добре запам’ятовувались.)
Так як сказав М.М.Мойсеєв
«Математика – один з листків, що об’єднують гуманітарне і природничо - наукове мислення».
А відомий вчений математик наш А.М.Колмогоров сказав:
«Ми абсолютно впевнені, що сьогодні віршознавство без математики вже не можливе»
На березі річки тополя росла,
Та вітру порив її стовбур зламав,
Тополя упала, і стовбур її
Кут прямий з течією ріки утворив.
Пам’ятай, в тому місці ріка
4 фути була шириною.
Верхівка схилилась до краю,
Залишивши 3 фути всього над водою.
Прошу, тепер швидше скажи мені ти:
Тополя якої була висоти?
IV.Практична задача:
Знайти висоту будівлі.
Знайти ![]()
![]()
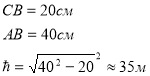
V.Підсумок уроку:
Чи потрібна теорема Піфагора В практичній діяльності людини?
Де застосовують теорему Піфагора?
Теорема Піфагора - основа евклідової геометрії. Завдяки їй доводиться більшість теорем геометрії.
Коли була відома ця теорема?
За 1000 років до Піфагора в Древньому Вавилоні та Єгипті. А Піфагору належить лише заслуга у доведенні і широке застосування при розв’язуванні задач.
V.Домашнє завдання:
Скласти задачу на теорему Піфагора з своєї практики.
№57


про публікацію авторської розробки
Додати розробку
