Застосування теореми Вієта

1. Доведіть, що корені рівняння    a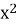+ bx + a = 0  -  обернені один до одного.

Якщо рівняння має корені, то за теоремою Вієта   * = = 1.

 За означенням, і – обернені числа.

2. При якому значенні m різниця коренів рівняння 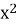+ mx + 1 = 0    дорівнює 1?

За теоремою Вієта 

=,

  ₊ 2 + = ,

 ( - 2 + ) + 4 =

=, 

= – 4.

За умовою = 1, то – 4 = 1, 

= 5,

= + .

Відповідь. + .

3.При якому значенні m сума квадратів коренів рівняння - 5mx + 4= 0

 дорівнює 68 ?

За теоремою Вієта   

₊ 2 + =25

+ = 25 - 8 = 17 .

За умовою 17 = 68,

= 4,

m = + 2.

Відповідь. + 2.

4. При якому значенні m один з коренів рівняння 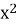- 12x + 9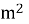= 0  є квадратом другого кореня ?

За теоремою Вієта 

За умовою =  , то   + = 12,

+ – 12 = 0,    

   або  

= .

-4 * 16 = - не має розв’язку.

3*9 = ,

= 3,

= + .

Відповідь. + .

5. При якому значенні m сума квадратів коренів рівняння 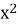+ mx + m - 2 = 0 найменша?

За теоремою Вієта  

+ = – 2 ( ) = - 2 + 4 = ( - 2 + 1 ) + 3 = ( + 3.

Оскільки  ( + 3 ˃ 0, то найменше значення буде  при = 1.

Відповідь. 1.