Завдання для підготовки до ДПА у форматі ЗНО
ВАРІАНТ 1
Частина перша
Завдання 1.1 – 1.20 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Запишіть 7
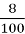 км у метрах.
км у метрах.
|
А) 7008 м |
Б) 7800 м |
В) 7080 м |
Г)7800 м |
- Обчисліть значення виразу -0,1+9m , якщо m= -0,1
|
А) 1 |
Б) -1 |
В) 0,9 |
Г) -0,9 |
- Розв’яжіть рівняння -10|x|+13=38.
|
А) 2,5 |
Б) -2,5 |
В) 2,5;-2,5 |
Г) немає розв’язку |
- Знайдіть нулі функції y=x2-5x+4.
|
А) -5;4 |
Б) -1 |
В) 0,9 |
Г) -0,9 |
1.5 Скоротіть вираз ![]() :
:![]()
|
А) x+5 |
Б) x-5 |
В) 1 |
Г) 0 |
- Знайти площу паралелограма,якщо відомо,що його сторони дорівнюють 5 см і 8 см,а кут між ними 135º.
|
А) 20 см2 |
Б) |
В) 10 |
Г) 10 |
- Знайти найбільший кут трикутника 5см,12см і 13 см?
|
А) 60º |
Б) 90º |
В) 115º |
Г) 135º |
-
Чому дорівнює скалярний добуток двох перпендикулярних векторів
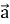 та
та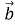 ?
?
|
А) -1 |
Б) 0 |
В) 1 |
Г) невідомо |
-
Внесіть під корінь -8
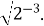
|
А) |
Б) |
В) |
Г) 1 |
- Знайдіть відстань між точками А(0;1) та В(2;-5).
|
А) 4 |
Б) 40 |
В) 2 |
Г) |
- У корзині 12 куль,з них три білі,сім червоних,дві чорного кольору.Яка ймовірність витягнути білу або чорну кулю?
|
А) |
Б) |
В) |
Г)Визначити неможливо |
1.12 Знайдіть радіус кола,якщо його довжина 16π.
|
А) 8 |
Б) 16 |
В) |
Г) |
1.13 Розв’язати нерівність –x2+2x-5 > 0.
|
А) (-∞;+∞) |
Б) [-1; +∞) |
В)[ -∞;+∞] |
Г) немає розв’язку |
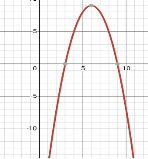
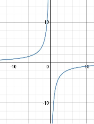
1.14 Вказати графік зображений на малюнку.
|
А) y=(x+6)2 +9 |
Б) y=-(x+6)2 +9 |
В)y=(x-6)2 +9 |
Г) y=-(x-6)2+9 |
1.15 Знайти суму абсцис точок перетину двох графіків y=2x+1 та у=![]() .
.
|
А) 1 |
Б) 0,5 |
В)-0,5 |
Г) -1 |
-
1.16 Чому дорівнює кутовий коефіціент для графіка y=-2x+5.
|
А) 2 |
Б) -2 |
В)-2,5 |
Г) 5 |
1.17 На уроці з гімнастики учитель записував результати минулих змагань і отримав таку вибірку 1 місце,3 місце,2 місце,1 місце,1 місце,3 місце,2 місце,2 місце,1 місце.Знайдіть моду даної вибірки.
|
А) 0 |
Б) 1 |
В)2 |
Г) 3 |
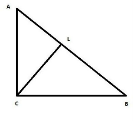 1.18 Дано прямокутний трикутник АВС,його катет АС=4 см,а проекція цього катета AL=2 см,СL-висота проведена до гіпотенузи. Знайти довжину гіпотенузи.
1.18 Дано прямокутний трикутник АВС,його катет АС=4 см,а проекція цього катета AL=2 см,СL-висота проведена до гіпотенузи. Знайти довжину гіпотенузи.
|
А) 16 |
Б) 8 |
В)4 |
Г) 3 |
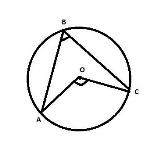 1.19 Дано коло та
1.19 Дано коло та ![]() ABC=76º.Знайти
ABC=76º.Знайти ![]() АОС.
АОС.
|
А) 38º |
Б) 114º |
В)152º |
Г) невідомо |
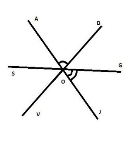 1.20 Дано
1.20 Дано ![]() AOD=84º,а
AOD=84º,а ![]() GOJ=53º.Знайти кут SOV.
GOJ=53º.Знайти кут SOV.
|
А) 43º |
Б) 96º |
В)127º |
Г) невідомо |
Частина друга
У завданнях 2.1 – 2.4 до кожного з чотирьох рядків інформації підберіть ЛИШЕ ОДИН ПРАВИЛЬНИЙ ВАРІНТ ВІДПОВІДІ.
2.1 Встановіть відповідність між функцією (1-4) та її графіком (А- F) .
1. y = ![]() ;
;
2. y=|x|;
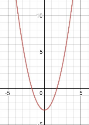
![]()
![]() 3. y=
3. y=![]() ;
;
![]()
![]()
![]() 4. y=
4. y=![]() -3;
-3;
![]()
|
|
А |
B |
C |
D |
F |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
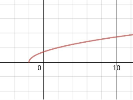
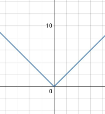
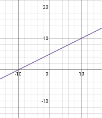
2.2 Встановіть відповідність між виразами (1-4) та їх значеннями(А- F) при а=3.
|
|
А |
B |
C |
D |
F |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
1.![]() A) 2;
A) 2;
2. (а2)5:а7 B)27;
3. 2а-4 C) 16;
4. а2+2а+1 D) ![]() ;
;
F) 1;
2.3 Встановіть відповідність між формулами площ (1-4) та фігурами (А- F) для яких їх застосовують.
|
|
А |
B |
C |
D |
F |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
-
S=
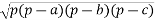 A)прямокутник;
A)прямокутник;
- S=πR2 B)трикутник;
-
S=
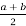 h C)трапеція;
h C)трапеція;
- S=ab D)коло;
F)квадрат;
2.4 Встановіть відповідність,між (1-4) та (А- F)
|
|
А |
B |
C |
D |
F |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
1. сos 30° А) sin 60° ;
2. sin 45° B) sin 30° ;
3. cos 60° C) 1;
4. sin 90° D) cos 45° ;
F) sin 0 ;
Частина третя
У завданнях 3.1 – 3.9 запишіть одержанні числові розв’язки у бланк відповідей.
3.1 На одній стороні трикутника взяли n точок, на другій – m точок і на третій k точок, причому жодна з них не збігається з вершинами трикутника.
1.Скільки є трикутників з вершинами в цих точках ?
2.Скільки є чотирикутників з вершинами в цих точках ?
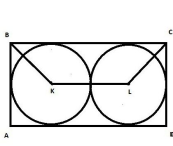 3.2 У прямокутник ABCD вписано два кола із центрами K та L,кожне з яких дотикається до трьох сторін прямокутника та одне до одного.Сума довжин вписаних кіл дорівнює 32π.
3.2 У прямокутник ABCD вписано два кола із центрами K та L,кожне з яких дотикається до трьох сторін прямокутника та одне до одного.Сума довжин вписаних кіл дорівнює 32π.
1.Визначте довжину відрізка KL.
2.Визначте площу чотирикутника BKLC.
3.3 Третій член арифметичної в чотири рази більший за перший член.Визначте різницю арифметичної прогресії,якщо сума перших п’яти членів дорівнює 220.
3.4 Майстер виготовляє 80 деталей у 8 разів швидше,ніж учень виготовсяє 480 сторінок.Скільки сторінок виготовить учень за той самий час,за який майстер зробить 320 деталей.
3.5 Розв’яжіть систему нерівностей
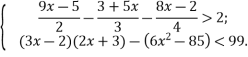
3.6 Знайдіть суму цілих значень x,що входять до області визначення функції y=![]() .
.
3.7 Діагональ рівнобічної трапеції ділить навпіл її тупий кут,а середню лінію трапеції на відрізки 6 см і 7 см. Знайдіть периметр трапеції.
3.8 Розв’яжіть нерівність ![]() ,але у відповідь запишіть найменший цілий розв’язок.
,але у відповідь запишіть найменший цілий розв’язок.
3.9 При якому найменшому додатному значенні параметра a система 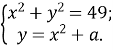 має єдиний розв’язок.
має єдиний розв’язок.


про публікацію авторської розробки
Додати розробку
