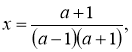Завдання І етапу Всеукраїнських учнівських олімпіад з математики

Про матеріал

Даний матеріал стане у нагоді вчителям математики ,при підготовці учнів до учнівської олімпіади з математики в 5-11 класах.

Перегляд файлу

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 5 клас

У гаманці в Семена три купюри : 1 гривня, 2 гривні і 5 гривень. Яку ціну, із запропонованих у відповіді, Семен не може заплатити без здачі? Відповідь поясни.

А : 3 гривні; Б : 4 гривні; В : 6 гривень; Г: 7 гривень; Д : 8 гривень.

7 б

За квадратний стіл можуть сісти четверо людей ( з кожного боку по одному ). Школярі до дня іменинника зсунули разом сім однакових столів так, що вони утворили один довгий прямокутний стіл. Скільки учнів може сісти за цей стіл?

7 б

Куб, виміри якого 10 см х 10 см х 10 см помістили в посудину з фарбою. Після того , як він висох, його розрізали на кубики з ребром 1 см . Скільки кубиків мають тільки дві пофарбовані грані?

7 б

Відновити пропущені цифри.

7 б

(рос)

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 5 клас

В кармане у Семёна три купюры: 1 гривна, 2 гривны и 5 гривен. Какую из предложенных вариантов цены он не сможет заплатить без сдачи. Ответ обоснуй.

А : 3 грн; Б : 4 грн; В : 6 грн ; Г: 7 грн ; Д : 8 грн .

7 б

За квадратным столом могут сесть 4 человека(с каждой стороны по одному). Школьники на день именинника сдвинули 7 столов.Сколько человек может поместиться за этим большим столом?

7 б

Куб, измерения которого 10 см х 10 см х 10 см поместили в посудину с краской. После того как он высох,его разрезали на кубики с ребром 1см. Сколько кубиков имеют только две окрашенные грани?

7 б

Восстанови пропущенные цифры.

7 б

(рос)

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 6 клас

	В феврале какого-то года 2419200 секунд. Высокосный ли этот был год? ( В високосном году 366 дней, в других – 365 дней).	7б
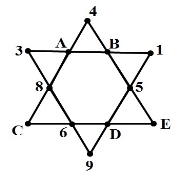
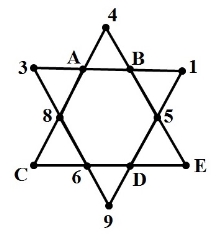
	Натуральные числа от 1 до 12 размещены на вершинах фигуры,таким образом, что суммы четырёх чисел на одной прямой равны. На какой вершине будет находиться число 7? $C:\Users\User\Pictures\UJJDJKJVRF.jpg$	7б
	На аллее от дома до озера растет 17 деревьев. Юрий, уходя из дома к озеру, отметил мелом первое дерево, а затем каждое второе дерево. На обратном пути к дому он снова отметил первое дерево (от озера), а затем каждое третье дерево. Сколько деревьев осталось неотмеченный?	7б
	Есть две кучки камней по 13 в каждой. За ход разрешается взять любое количество камней, но только с одной кучки. Проигрывает тот, кому нечего брать. Кто обеспечит себе победу в этой игре?	7б

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 6 клас

1	У лютому деякого року 2419200 секунд. Чи високосним був цей рік? (У високосному році 366 днів, в інших – 365 днів).	7б
2	$C:\Users\User\Pictures\UJJDJKJVRF.jpg$ Натуральні числа від 1 до 12 розміщені на вершинах фігури, зображеної на малюнку таким чином, що суми довільних чотирьох чисел, розміщених на одній прямій, є однаковими. Де знаходиться число 7?	7б
3	На алеї від будинку до озера росте 17 дерев. Юрко, ідучи з дому до озера, відмітив крейдою перше дерево, а потім кожне друге дерево. На зворотному шляху до будинку він знову відмітив перше дерево (від озера), а потім кожне третє дерево. Скільки дерев залишилось невідміченими?	7б
4	Є дві купки камінців по 13 в кожній. За хід дозволяється взяти будь-яку кількість камінців, але тільки з однієї купки. Програє той, кому нема що брати. Хто може забезпечити собі перемогу в цій грі?	7б

(рос)

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 7 клас

Есть две кучки камней по 13 в каждой. За ход разрешается взять любое количество камней, но только с одной кучки. Проигрывает тот, кому нечего брать. Кто обеспечит себе победу в этой игре?

7б

Какой день недели был вчера, если четверг был за четыре дня до послезавтра ?

7б

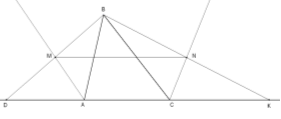
Фигуры 1, 2, 3, 4, 5 - квадраты. Периметр квадрата 1 равна 12 см. Найдите периметр квадрата 5.

7б

Решите уравнение: |14 - |2x+3||=5.

7б

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 7 клас

Є дві купки камінців по 13 в кожній. За хід дозволяється взяти будь-яку кількість камінців, але тільки з однієї купки. Програє той, кому нема що брати. Хто може забезпечити собі перемогу в цій грі?

7б

Який день тижня був учора, якщо четвер був за чотири дні до післязавтра?

7б

Фігури 1, 2, 3, 4, 5 – квадрати. Периметр квадрата 1 дорівнює 12 см. Знайдіть периметр квадрата 5.

7б

Розв’язати рівняння: |14 - |2x+3||=5.

7б

(рос)

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 8 клас

	Клоун сказал, что количество котят, которые живут у него равно их количества и еще котенка. Слова «котенка» вызвали смех. Однако клоун сказал правду. Сколько котят живет у нем?	7б
	Саша, Борис и Василий собирали грибы. Борис нашел грибов на 20% больше, чем Саша, но на 20% меньше, чем Василий. На сколько процентов больше грибов нашел Василий, чем Саша?	7б
	Решите уравнение: *в зависимости от* а.	7б
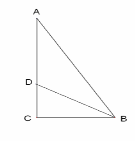
	В прямоугольном треугольнике катет длиной 12см прилегает к углу Найти длину биссектрисы второго острого угла треугольника.	7б

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 8 клас

1	Клоун сказав, що кількість кошенят, які мешкають у нього дорівнює їх кількості і ще кошеняти. Слова « кошеняти» викликали сміх. Проте клоун сказав правду. Скільки кошенят мешкає у нього?	7б
2	Сашко, Борис і Василь збирали гриби. Борис знайшов грибів на 20% більше, ніж Сашко, але на 20% менше, ніж Василь. На скільки відсотків більше грибів знайшов Василь, ніж Сашко?	7б
3	Розв’язати рівняння: *залежно від а.*	7б
4	У прямокутному трикутнику катет завдовжки 12см прилягає до кута Знайти довжину бісектриси другого гострого кута трикутника.	7б

Завдання І етапу Всеукраїнських учнівських олімпіад з математики 9 клас

	Зал кінотеатру містить місць, які поділені між трьома секторами – центральним та двома однаковими – правим та лівим. Усі сектори містять по рядів. В центральному секторі по 28 місць в кожному ряду. Скільки місць у кожному ряду в правому та лівому секторах, якщо їх однакова кількість у кожному ряду?	7б
	При яких значень параметра а рівняння 2х²-4(+1)х+4+1=0 має єдиний розв’язок?	7б
	На автомобілі нові шини. Шина на задньому колесі витримує пробіг 16000 км, а на передньому – 24000 км. Який максимальний шлях можна проїхати на цих шинах?	7б
	Дано трикутник АВС зі сторонами Провели бісектриси зовнішніх кутів при вершинах А та С і з вершини В на них опустили перпендикуляри ВМ і BN. Знайти довжину відрізка MN.	7б

Завдання І етапу Всеукраїнських учнівських олімпіад з математики

10клас

1.	Четверо хлопців помітили, що якщо вони складуть всі свої гроші без першого, то зберуть 90 грн, без другого - 85, без третього - 80, без четвертого - 75 грн.. Скільки у кожного грошей?	7б
2.	Розв’яжи рівняння \|x-1\|+\|x-2\|=x+3.	7б
3.	При яких значень параметра а рівняння 2х²-4(+1)х+4+1=0 має єдиний розв’язок?	7б
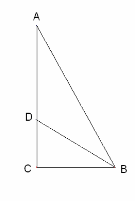
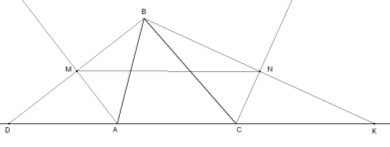
4.	Дві висоти ромба, проведені з вершин його тупих кутів, перетинаються та діляться у відношенні 1:2. Знайти кути ромба.	7б

ВІДПОВІДІ:

клас

№ завдання

Відповідь

клас

12*8=96 Вказівки:у кожного ребра 8 (10-2=8два при вершині у них зафарбовано 3 сторони) таких кубів,всього ребер 12.

Відповідь:

			4	1	5
			3	8	2
			8	3	0
	3	3	2	0
1	2	4	5
1	5	8	5	3	0

клас

Відповідь: ні,не високосний. Число 2419200 ділиться на 7 (перевіряється безпосередньо). Отже, у лютому 28 днів, а рік – звичайний.

В точці Е

Другий гравець. Розв’язання. Другий гравець буде повторювати ходи першого, але братиме камінці з іншої купки. (Метод симетричної стратегії).

клас

П’ятниця

Відповідь: 96 см.

Розв’язання: Якщо периметр квадрата 1 дорівнює 12 см, то його сторона – 3 см (12 см : 4). Тоді сторона квадрата 2 – 6 см (3 см + 3 см), а сторона квдрата 3 – 9 см (6 см + 3 см). Сторона квадрата 4 – 15 см (9 см + 6 см). Тоді сторона квадрата 5 – 24 см (15 см + 9 см). Периметр квадрата 5 дорівнює 96 см

(24 см ∙ 4).

Відповідь: x=3, x= –6, x=8, x= –11

клас

3 кошеняти. Вказівка. Складемо рівняння: . Звідки .

на 50%. Вказівка. Нехай Борис зібрав х грибів, тоді Сашко – 0,8х, а Василь – 1,2х грибів. Василь зібрав на більше грибів, ніж Сашко.

Запишемо рівняння у вигляді:.Добуток дорівнює нулю при або , тому розглянемо такі випадки:1) при рівняння набуває вигляду , яке коренів не має;2) при дістанемо рівняння , корені якого - всі числа;3) при , тому .Відповідь. При ; при корені рівняння — всі числа; при коренів немає.

Рисунок3 Вказівка. Нехай в , бісектриса кута В, тобто , тоді рівнобічний і . З тому см, см, см

клас

Відповідь: .

Розв’язання.У центральному секторі усього місця. Тому в двох інших секторах – місць, тобто у кожному по . Оскільки там рівно однакових рядів, то у кожному по місць.

Розв’язання. Оскільки в умові не сказано, що рівняння є квадратним, то спочатку розглянемо випадок =0, тобто рівняння -4х+1=0, яке має один розв’язок х =.

Решту значень а отримаємо з умови D=0:

D=16(+1)²-4^.2^.(4+1),

2²-3-2=0; ₁= - і ₂=2.

Відповідь: при -, 0; 2.

RIS_88_1 Оскільки трикутники прямокутні, мають спільний катет та рівні кути, то вони рівні. Звідси випливає, що . Аналогічно, що . Отже, середня лінія .

Відповідь:

10 клас

Розв’язання. Хай в першого - x грн., в другого - y, в третього - z, в четвертого - t. Умови завдання визначають, що має місце система рівняння

y + z + t = 90 x + z + t = 80 x + y + t = 85 x + y + z =75 (3б)

Склавши всі рівняння , отримуємо, що 3(х + y + z + t) = 330,(4б) так що х + y + z + t = 110. Віднімаємо з 110 послідовно 90, 85, 80, 75 знаходимо х, y, z, t. (5б) (Відповідь: 20, 25, 30, 35 )

Решение. Корни выражений, стоящих под модулем, — 1 и 2. Числовая ось разбивается точками 1 и 2 на три промежутка,

Рассмотрим каждый из этих случаев.

1) Поскольку оба выражения, стоящие под модулем, неотрицательны на рассматриваемом промежутке, исходное уравнение преобразуется к виду x-1+x-2=x+3. Решение этого уравнения x=6. Этот корень попадает на промежуток и поэтому является решением исходного уравнения.

2) Поскольку первое выражение, стоящее под модулем, положительно, а второе отрицательно на рассматриваемом промежутке, то исходное уравнение преобразуется к виду x-1+2-x=x+3. Решение этого уравнения x=-2. Поскольку -2 не попадает на рассматриваемый промежуток [1,2), то этот корень — посторонний.

3) Поскольку оба выражения, стоящие под модулем, отрицательны на рассматриваемом промежутке, исходное уравнение преобразуется к виду 1-x+2-x=x+3. Решение этого уравнения x=0. Этот корень принадлежит промежутку и является решением исходного уравнения.

Ответ. {0;6}.

Решту значень а отримаємо з умови D=0:

D=16(+1)²-4^.2^.(4+1),

2²-3-2=0; ₁= - і ₂=2.

Відповідь: при -, 0; 2.

Розв’язання. Розглянемо . В нього катет вдвічі менше за гіпотенузу , тому . Тому друга пара кутів ромба складає . ( Відповідь: . )

Орієнтовні критерії оцінювання олімпіадної роботи

7	Повне правильне розв’язання завдання
6	Повне правильне розв’язання. Є недоліки, які в цілому не впливають на розв’язання
5	Розв’язання в цілому вірне. Однак воно містить ряд помилок, або не розглянуті окремі випадки. Але воно може стати правильним після невеликих виправлень або доповнень
4	Правильно розглянуто один з істотних випадків, вірно проведене дослідження або пояснення, частково розв’язане завдання
3	Доведені допоміжні твердження, вірно розпочато розв’язування
2	Розглянуто окремі важливі елементи розв’язання, або почато розв’язування завдання з подальшим невірним розв’язком
1	Розв’язуване завдання виконано з грубими помилками, які призвели до неправильного результату або присутня лише ідея розв’язку
0	Початок виконання завдання неправильний або до виконання завдання не приступав

docx

Завантажити

Зберегти на потім

Додав(-ла)

Шандиба Ірина Анатоліївна

Пов’язані теми

Математика, 7 клас, Інші матеріали

Додано

1 листопада 2021

Переглядів

9280

Оцінка розробки

Відгуки відсутні