Відділ освіти

П’ятихатської районної адміністрації

Дніпропетровської області

Комісарівська загальноосвітня школа І-ІІІ ступенів

П’ятихатської районної ради

Дніпропетровської області

 

 

 

 

 

 

 

 

 

 

Укладач : Гаркуша Н.Д.– вчитель математики  Комісарівської ЗШ  І-ІІІ ст.

 

 

 

 

 

 

 

 

 

 

 

 

 

Сучасна математика знає безліч функцій, і в кожної свій неповторний вигляд, як неповторний вигляд кожного з мільярдів людей, що живуть на Землі. Однак при всій несхожості однієї людини на іншу у кожної є руки і голова, вуха і рот. Точно так же вигляд кожної функції можна представити складеним з набору характерних деталей. Функції - це математичні портрети стійких закономірностей, пізнаваних людиною. В запропонований збірці  описані властивості усіх функцій  навчальної програми курсу математики 7-11  класів, а також їх практичне застосування.

Використання представленого матеріалу  сприяє  підвищенню зацікавленості та розвиток креативного мислення учнів, формуванню  їх пізнавальних інтересів, формуванню компетенцій саморозвитку та самоосвіти.

 

 

Між планетами, між породами,

Між рослинами, між народами

Випадково чи з необхідності –

Скрізь простежуються відповідності.

Поміж зграями і кошарами,

Між суспільствами і державами,

І в конструкціях, і в інструкціях -

Відповідності, тобто функції.

Від мікробини до безмежності

Скрізь залежності і залежності.

Від ціни на газ, на одежину

Ми залежимо, ще й як залежимо!

Там – від долара, там – від унції…

А залежності – також функції.

 

 

 

 

 

   Поняття функції пройшло складний шлях від функцій, які лише з малим ступенем точності моделювали кількісні закономірності найпростіших ситуацій, до функцій, які характеризують закономірності надзвичайно складних явищ на різних рівнях організації матерії.

   Ще в 16 столітті в математиці не було загальної символіки. Кожна операція записуваласьповністю словами або спеціальними знаками – скороченнями, що використовував тільки один або кілька вчених. Інші вчені усе писали словами або застосовували свої скорочення. Невідомі коефіцієнти і вільний член рівняння також не мали загальновизнаних умовних позначень.

З 17 століття починається суттєво новий період розвитку математики. Французькі вчені Франсуа Вієт і Рене Декарт розробили буквену математичну символіку, що незабаром дістала загальне визнання.

Введено було спільне позначення невідомих – останніми буквами латинського алфавітуx, y, zвідомих – початковими буквами того ж алфавіту a, b, c,… і т. ін.

Під кожною буквою стало можливим розуміти не тільки те, що дано в умові задачі, але і багато інших значень, допустимих змістом задачі. Після введення буквеної символіки стало можливим записати розв’язок цієї задачі у вигляді загальної формули. Наприклад, s=vt, де під s слід розуміти шлях, пройдений екіпажем, під v – швидкість,t - час.

Таким чином, разом з буквеною символікою в математику прийшла ідея змінних, оскільки під кожною буквою стало можливим розуміти різні значення.

Розвиток капіталізму в Європі, перехід від ремесла і ручного мануфактурного виробництва до виробництва з машинною технікою, розвиток мореплавання – усе це надавало життю руху вперед. Тож від математики очікували відповідей на ряд важливих запитань. Багатих купців цікавили найкоротші і безпечні шляхи в Америку, збільшення швидкості і вантажності суден, точні способи орієнтування у відкритому морі і т. ін..

Дати вірні і переконливі відповіді на ці запитання можна було тільки за допомогою математики.

Але математика була не в змозі задовольнити такі потреби життя, бо методи, якими вона користувалася виявилися недостатніми. Потрібний був значний поворот, необхідні були нові прийоми дослідження, за допомогою яких вона б відповідала запитам життя.

І нове велике відкриття було зроблено.

До початку 17 століття алгебра була вже досить розвинутою наукою. Працями багатьох поколінь учених були підготовлені умови для нового великого відкриття в науці, що послужили б поштовхом до її подальшого розвитку. Таким відкриттям стало введення в математику поняття змінної величини і прямокутної системи координат.

Увів у математику функціональну залежність французький вчений Рене Декарт. Він був великим і різнобічним ученим: займався філософією, фізіологією, фізикою, математикою. У математиці він зробив багато різних відкриттів і нововведень, але найбільшою його заслугою є введення в математику поняття змінної величини і функції, що він їх виклав у книзі «Геометрія», виданій у 1637 році. Це відкриття назвали «поворотним пунктом у математиці». Декарт ввів систему прямокутних координат, якою користуємося ми, в широке застосування і поклав початок розвиткові важливої математичної науки – аналітичної геометрії. Працями Декарта алгебру було значно вдосконалено. Термін «функція», що в перекладі з латинської мови означає виконання, здійснення Р.Декарт не вживав.

Термін «функція» вперше зустрічається в листі німецького математика Г. В. Лейбніца до голландського математика Х. Х. Гюйгенса в 1694 році. У загальне вживання термін введено на початку 18 століття Йоганном Бернуллі. З цього часу починає розвиватись ціла теорія функцій З’явилось вчення про тригонометричні функції, яке набуло сучасного вигляду в працях Леонарда Ейлера (1707 -1783). Л.Ейлер також ґрунтовно досліджував показникові й логарифмічні функції.

Найзагальніше сучасне означення функції сформульовано в працях Ніколя Бурбакі. Це псевдонім, під яким велика група французьких математиків друкувала свої праці в 1937 – 1968рр.

На початку 19 століття ученим довелося досліджувати явища, які було зручніше описувати мовою недиференційованих функцій. Так, надзвичайно нерегулярні траєкторії частинок у броунівському русі нагадують неперервні криві без похідних. Виявилося,що поняття неперервності й розривності функцій мають безліч прообразів у природі і відображають істотні моменти руху різних матеріальних утворень. Народження і смерть живого організму, спалах наднової, вибух ядра галактики і розпускання бутона, зміна агрегатного стану речовини і безліч інших явищ живої і неживої природи являють собою якісний стрибок, для вивчення кількісних характеристик якого і служать розривні функції. Нині бурхливо розвивається теорія катастроф – математичний апарат для вивчення стрибкоподібних змін у русі певних систем, порушення неперервності якогось процесу.Була розвинута теорія еліптичних функцій Н.Абелем і К.Якобі. Надалі геометричні ідеї Б.Рімана стали більш визнаними як стиль мислення в області теорії функцій комплексної змінної. За допомогою даної теорії було розв’язано багато задач аеро- і гідродинаміки, теорії пружності, радіотехніки і багато ін..

В період захоплення теорією функцій комплексної змінної найбільш видатним представником у питаннях теорії функцій дійсного числа був російський математик П.Л.Чебишев.

Ф.Клейн і А.Пуанкаре створюють теорію автоморфних функцій, в якій знаходить застосування геометрія М.Лобачевського. Ж.Адамар, Е.Борель глибоко розробляють теорію цілих функцій.

Якщо раніше систематично вивчались лише функції, що виникають «безпосередньо» з тих чи інших спеціальних задач, для теорії функцій дійсного числа типовим є інтерес до повного вияснення всього об’єму загальних означень і узагальненню основних понять.

Основи сучасної теорії функцій дійсного числа були закладені математиками французької школи: К.Жорданом, Е.Борелем, А.Лебегом, Р.Бером. Вироблені методи теорії функцій дійсного числа виявились особливо необхідними при побудові основ функціонального аналізу.

Ініціатором уведення поняття функції у шкільний курс математики був відомий український математик Михайло Васильович Остроградський (1801-1862), уродженець с.Пашенна Кобеляцького повіту на Полтавщині.Ще в середині 19 ст., майже на 50 років раніше від німецького математика Ф.Клейна, він висловив ідеї, які згодом лягли в основу міжнародного руху за реформу навчання в школах. Оригінальні підручники з тригонометрії надрукував відомий український математик Микола Андрійович Чайковський (1887-1970), який народився в м.Бережани Тернопільської області. Плідно працював у галузф теорії функцій український математик Михайло Пилипович Кравчук(1892-1942рр.), що народився в с. Човниці на Волині.

Розвиток сучасної математики неможливо уявити без диференціального та інтегрального числення та без теорії функцій вцілому.

 

 

Лінійна функція

Лінійною називається функція, яку можна задати формулою y = kx+b , де х — аргумент, а k і b — дані числа.

Графік лінійної функції — пряма. k називається кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до осі абсцис,— графік деякої лінійної функції.

Через дві точки можна провести одну й тільки одну пряму, тому для побудови графіка лінійної функції досить знати координати двох його точок (дуже добре, якщо це будуть точки перетину графіка з осями). Точка перетину графіка з віссю абсцис має ординату 0, а точка перетину графіка з віссю ординат має абсцису 0.

Лінійна функція є аналітичним записом:
	Залежність між швидкістю і часом для рівномірно прискореного руху
	Залежність довжини стержня від його температури
	Закон Гей-Люссака, де V – об’єм газу зі сталим тиском, -біном об’ємного розширення;
	Закон Шарля, р – тиск газу зі сталим об’ємом
	Калорійність молока, де р – жирність молока в %, к – добовий надій молока в кг, Q – кількість ккал у добовому надої
	Коефіцієнта тертя гальмівної колодки, v – швидкість руху потяга
	Опора дороги з асфальтовим покриттям, v – швидкість руху автомобіля

 

Прямa  пропорційність

Лінійну функцію, що задається формулою y = kx , де , називають прямою пропорційністю.

Графік прямої пропорційності — пряма, що проходить через початок координат. Якщо х>0, графік лежить у I і III координатних чвертях, а якщо х<0 — то у II і IV координатних чвертях.

 

 

 

 

 

 

 

 

 

 

 

Пряма пропорційність широко використовуються для аналітичного запису багатьох фізичних величин:

	Залежність між масою та об’ємом за сталої густини
	Залежність між вагою тіла і масою
	Залежність між шляхом і часом при рівномірному русі
	Залежність між вартістю і кількістю купленого товару
	Залежність між довжиною кола та діаметром	C
	Залежність сили пружності від деформації
	Залежність заряду конденсатора від напруги в ньому
	Залежність напруги на кінцях провідника від сили струму
	Залежність потоку магнітної індукції, який пронизує контур, від сили струму в ньому

 

 

 

Обернена пропорційність

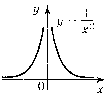
Функцію, задану формулою y=k/x, де х — незалежна змінна, k≠0 — дане число, називають  оберненою пропорційністю.

Область визначення функції y=k/x — множина всіх чисел, крім 0.

Графік функції y=k/x, ( k≠0) — гіпербола, симетрична відносно початку координат. Коли k>0, гілки такої гіперболи розміщені в I і III координатних кутах, коли k<0 — у II і IV.

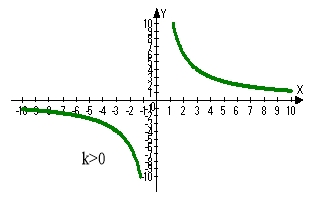
Графік функції  нескінченно наближається до осей координат, але не перетинає їх. Дійсно, x=0 не входить до області визначення, отже точки перетину з віссю Oy немає. k/x≠0 ні при якому значенні х, значить, якщо x≠0, точки перетину з віссю Ox немає.

 

 

 

Функція у=k/х виражає залежності між різними змінними:

а) часу від швидкості при рівномірному русі;

 б) кількості купленого товару на задану суму грошей від ціни товару;

 в) сили струму від опору провідника при сталій напрузі;

 г) між тиском газу і об’ємом, який він заповнює та ін...

 

 

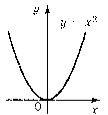
Функція у=х²

Область визначення цієї функції — множина всіх дійсних чисел.

Графік проходить через початок координат O(0;0).

y(x)≥0 при всіх значеннях х. Усі точки графіка розташовані не нижче осі Оx.

Протилежним значенням аргументу відповідають рівні значення функції, тобто графік симетричний відносно осі ординат.

 

 

 

 

За допомогою цієї функції виражають залежність площі квадрата від довжини його сторін. На практиці у фізиці, техніці частіше застосовують функціюy=ax², де a – число. З її допомогою виражають: а) залежність площі круга від радіуса; б) між кінетичною енергією тіла і його швидкістю;

в) шляху вільно падаючого тіла від часу і т.д.

 

 

Квадратична функція

 

Функція виду у=ax²+bx+c, де х – змінна,  а, b, с – деякі числа, причому а≠0, називається  квадратичною функцією.

 

 

 

 

 

 

 

 

 

 

 

 

Властивості квадратичної функції

 

 

 

 

 

Застосування  квадратичної функції

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Властивості показникової функції	y=ax, a>1	y=ax, 0<a<1
Графік
1. Область визначення функції	D(f) = ( - ;+)
2. Область значень функції	E(f) = ( 0; + )
3. Парність, непарність.	Функція не є ні парною, ні непарною (функція загального вигляду).
4. Перетин з осями координат	Якщо х=0, то у=1, тобто графік проходить через точку (0;1)
5.Проміжки порівняння з одиницею	Якщо х<0, то у<1; Якщо x>0, то y>1.	Якщо х<0, то у>1; Якщо x>0, то y<1.
6. Проміжки знакосталості	f(x)>0, при будь-якому значенні аргументу
7.Монотонність	Монотонно зростає на R	Монотонно спадає на R

Показникова функція

 

 

 

Застосування показникової функції

Ріст народонаселення. Зміна числа жителів країни за невеликий відрізок часу  описується формулою N=N₀*e^at , де N₀ - число людей в момент часу t=0,  N – число людей в момент часу t,  a –стала.

Діагностика захворювань. При диагностиці  ниркових хвороб, часто визначають здатність нирок виводити  з  крові  радіоактивні  ізотопи, причому їх кількість в крові  зменшується по показниковому закону.

Барометрична  формула.  При постійній температурі тиск повітря зменшується із зменшенням висоти  над рівнем моря по закону

 p = p₀*e ^h/H,  где p₀ –тиск на рівні моря (h =0), p –тиск на высоті h, H - константа, якя залежить від температури повітря .

Формула разрядки конденсатора. Якщо початкова напруга на конденсаторі рівна  U₀, то конденсатор буде розряжатись  за  законом:  U=U₀*e ^t/RC,

  де t –час , протягом якого розряжається конденсатор, R –опір, C – електроємність конденсатора.

Радіоактивний роспад.

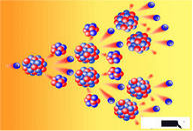Після відткриття радіоактивності в дослідах Беккереля і Кюрі  виникло питання , за яким законом відбувається розпад атомів? Виявилось, що кількість речовини, що розпадається за одиницю часу завжди  пропорційна даній кількості речовини.

Фізики назвали проміжокчасу, протягом якого роспадається половина всіх даних атомів, періодом напіврозпаду даної речовини. Цей період  різний  для різних  речовин: для урану - 238 він рівний 4,5 млрд років, для радію – 1620 років, для полонію – 84 роки, для цезію-137 – 31рік,  для йоду - 131 – 8 діб.

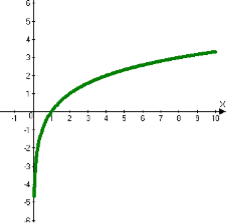
Логарифмічна функція

 

Властивості логарифмічної функції	, a>1	, 0<a<1
Графік
1. Область визначення функції	D(f) = ( 0; + ∞)
2. Область значень функції	E(f) = ( -∞;+∞)
3. Парність, непарність.	Функція не є ні парною, ні непарною (функція загального вигляду).
4. Перетин з осями координат	Якщо х=1, то у=0, тобто графік проходить через точку (1;0)
5. Проміжки знакосталості	Якщо х>1, то f(x)>0; Якщо х<1, то f(x)<0.	Якщо х>1, то f(x)<0; Якщо х<1, то f(x)>0.
6.Монотонність	Монотонно зростає на  R	Монотонно спадає на R

 

 

Застосування логарифмічної функції

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.

 Рівняння (в полярних координатах) має вигляд: .

Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.

ФІЗИКА

Фізика  завжди вимагає математичних розрахунків, тому знання математики у фізиці завжди необхідне. Ось декілька формул, де використовуються логарифми.

Робота, яку виконує газ при ізотермічному процесі

  

m – маса газу;

µ - молярна маса газу;

R – універсальна газова стала;

Т  – температура за Кельвіном;

V -  об’єм газу;

P – тиск газу.

ємність циліндричного конденсатора:

  

L – висота циліндра;

R, r – радіуси внутрішнього та зовнішнього циліндра;

 – техн. характеристики конденсатора;

Ємність дільниці одиничної довжини двох провідної лінії

  

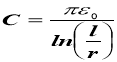
   r – радіус провідника

Зв’язок між сталою розпаду, середнім часом життя і періодом піврозпаду Т

  

    – середній час життя;

   Т – період піврозпаду;

Рівень інтенсивності звуку

  

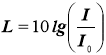
  - умовно нульовий рівень

Ентропія

  S=kln

К – стала Больцмана;

Ω - термодинамічна імовірність ;

S – ентропія;  

 

Зміна ентропії при ізотермічному стисканні газу

  

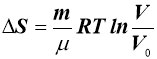
R – універсальна газова стала

µ - молярна маса газу

m – маса газу;

V – об’єм газу

 У техніці часто застосовуються ножі, що обертаються. Сила, з якою вони тиснуть на матеріал, що розрізається, залежить від кута розрізання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того, щоб тиск був сталим, потрібно щоб залишався сталим кут розрізання, а це буде у  тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Завдяки цьому лезо ножа сточується рівномірно.

    Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

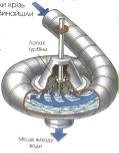
 У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

Хімія

  Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну,що характеризується різною концентрацією йонів Гідрогену С( Н⁺).Для зручності датським біохіміком С.Сьоренсеном у 1909 році було введено термін «водневий показник» (рН), –це значно спростило роботу багатьом поколінням хіміків. Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену

рН= - lg С( Н⁺)

 Значення рН може змінюватись від 1 до 14

 Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5. Відповідний вміст у них катіонів Н⁺ оптимальний для нашої шкіри.

   

 У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7).

БІОЛОГІЯ

 Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

       

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

МУЗИКА Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах: logNmp= m+ . Номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина).

Степенева функція

Значення параметра  р	Схематичне зображення графіка	Область визначення функції D(y)	Область значень функції E(y)	Парність (непар-ність)	Зростання (спадання)
р – додатне ціле парне, р = 2, 4, 12...		R	[0; +)	парна	спадає, якщо x(–;0], зростає, якщо x[0;+)
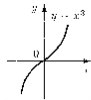
р -додатне ціле непарне, р = 1, 3, 9...		R	R	непарна	зростає
р –від’ємне ціле парне, р = -2; -4 ...		х0	(0; +)	парна	зростає, якщо x(–;0), спадає, якщо x(0;+)
р – відємне ціле непарне, р = -1; -3		х0	у0	непарна	спадає на проміжках (–; 0), (0; +)
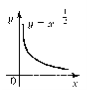
р – додатне раціональне, р = .		[0; +)	[0; +)	ні парна, ні непарна	зростає
р –від’ємне раціональне,р = - -		(0; +)	(0; +)	ні парна, ні непарна	спадає

 

Тригонометричні функції

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

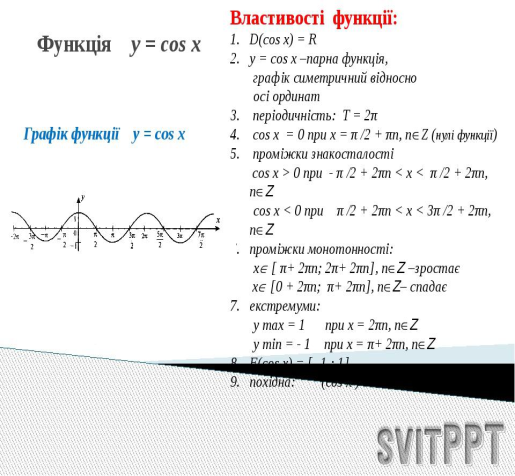
Різні коливання зустрічаються нам на кожному кроці. Механічні коливання застосовуються для швидшої закладки бетону спеціальними  машинами, для просіювання матеріалів на віброситах і навіть для майже безболісного свердлення дірок в зубах.

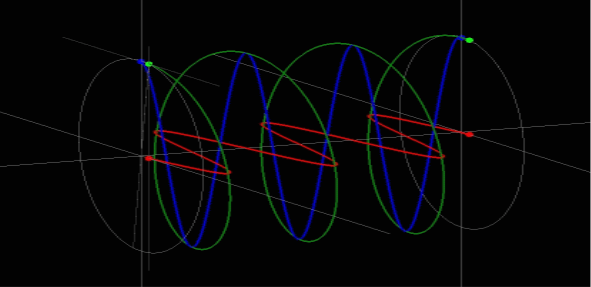
Акустичні коливання потрібні для прийому і одержання звуку, а електромагнітні  - для радіо, телебачення, зв’язку з космічними ракетами. Електромагнітні коливання доносять до нас звістки про складні процеси, які проходять всередині зірок, про вибухи у віддалених галактиках, про такі дивовижні речі, як пульсари, чорні дири і т.д. З допомогою електромагнітних  коливань вченими були одержані знімки зворотної сторони Місяцяи і вічно закритої хмарами Венери.

Коливання супроводжують і біологічні процеси, наприклад, слух, зір, передача збудження по нервовій тканині, роботу серця і мозку. Записуючи роботу серця і мозку, лікарі одержують електрокардіограми і енцефалограми.

 

Застосування тригонометричних функцій