Збірник "Застосування інтегралу до розв"язування задач практичного змісту"

Застосування інтегралу  до розв'язування задач практичного змісту

ПЕРВІСНА

Означення первісної

1.   Крапля дощу падає зі сталим прискоренням g = 9,8 м/с². Знайдіть вираз, який описує швидкість її падіння.
2.   Після удару м'яч рухається з прискоренням а(t) = 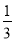t² (м/с²). Знайдіть вираз, який описує швидкість його руху.
3.   Куля вилетіла із ствола гвинтівки зі сталим прискоренням 5 м/с². Знайдіть вираз, який описує швидкість руху кулі.

Основна властивість первісної

1.   Швидкість приземлення парашутиста змінюється за законом V(t) = 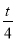- 1. Знайдіть залежність шляху S парашутиста від часу t , якщо за першу хвилину він знизився па 400 м.
2.   Спостерігач побачив падаючий метеорит, який впав на землю через 15 с. Швидкість метеорита змінювалася за законом V(t) = t²+ t і за першу секунду він пролетів 10 м. На якій висоті був метеорит, коли його побачив спостерігач ?
3.   Під час польоту лелеки його прискорення змінювалося за законом а(t) = t ² + t. Знайдіть залежність швидкості лелеки від часу, якщо в момент часу t = 3 хв. його швидкість становила 4 м/с.

Три правила знаходження первісних

1.   Швидкість руху тіла змінюється за законом V(t) = t²- t +1. Знайдіть закон руху тіла.
2.   Метелик рухається з прискоренням  а(t) = 3 соst. Знайдіть закон зміни швидкості руху метелика.
3.   Велосипедист рухається по прямій дорозі зі сталим прискоренням 12 м/с² Знайдіть швидкість руху велосипедиста, якщо в початковий момент відліку швидкість  V₀=  1 м/с.
4.   Швидкість руху потяга задається рівнянням V(t) = t²-4 t + 5. Знайдіть закон руху потяга.
5.   Швидкість руху ластівки задасться рівнянням V(t) = 7t²- - 1. Знайдіть рівняння руху ластівки, якщо в момент часу t = 2с шлях S = 12 м.             

ІНТЕГРАЛ

Формула Ньютона-Лсйбніца

1.    Cнаряд після вистрілу з гармати летить зі швидкістю V = (2,5 + 0,2 t)м/c. Яку відстань пролетить снаряд за 10с руху?
2.    З вертольота скинуто вантаж, який рухається прямолінійно зі швидкістю                            V = (t + 6 t²) м/с. Який шлях пройде ватаж за третю секунду?
3.    Швидкість автомобіля під час гальмування задасться формулою V = (18 - 1,2 t) м/с. Який гальмівний шлях пройде автомобіль, якщо він зупинився через 15с після початку гальмування?
4. Bизначте кількість електрики, яка проходить через поперечний переріз провідника за 3с. якщо сила струму змінюється за законом                            I(t) = (4 t ² + 7t + 9) А.
5.    Два боліди на старті гонок почали рухатися одночасно по прямій. Перший болід рухається зі швидкістю V = 3t² м/с, другий - зі швидкістю V= (6 t² - 10) м/с. На якій відстані один від одного вони будуть через 10с ?
6.    Обчисліть площу аркуша паперу, який мас форму криволінійної трапеції, обмеженої лініями у = 4х - х², у = 0, х = 5.
7.    Знайдіть момент інерції відносно центра мас однорідного стержня завдовжки І.
8.    Ширина річки дорівнює 10м. Контур поперечного перерізу річки мас вигляд параболи у= 0,12х². Визначте об'єм води, яка проходить через поперечний переріз за 1с, якщо швидкість течії дорівнює 1,1 м/с.
9.    Ділянка землі обмежена з одного боку дорогою, а з іншого - річкою, яка має форму параболи у = 8/17 х². Дорога перетинається з річкою в двох місцях, відстань між якими 3 км. Знайдіть площу ділянки землі.
10. Тіло рухається з прискоренням а =7 м/с². Який шлях пройде тіло за перші 20с ?

11. Однорідний мідний стержень завдовжки 1м рівномірно обертається навколо вертикальної осі, яка проходить через один з його кінців. За якої швидкості обертання стержень розірветься ?

12. Опора, виготовлена з десяти міліметрового сталевого листа, мас форму криволінійної трапеції, обмеженої лініями у = 8 - 2х² і у = 4 – х². Знайдіть масу опори, якщо густина сталі 7760 кг/м³.
13. Санки рухаються горизонтально по льоду зі швидкістю 5 м/с і виїжджають на дорогу. Визначити шлях, який пройдуть санки по дорозі, якщо їхня довжина 1м, а коефіцієнт тертя саней по дорозі 0,5. Тертям саней по льоду знехтувати.
14. Експериментально встановлено, що залежність витрати бензину на 100 км шляху від швидкості автомобіля визначається формулою Q = 18 – 03V+ 0,003V², де

30  V  110. Визначте середню витрату бензину за швидкості руху 50 - 60 км/год.

ІНТЕГРАЛ

Площа криволінійної трапеції.

1. Обчисліть площу ігрового майданчика, який має форму криволінійної трапеції, обмеженої лініями у = 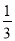 х²,    х = 2, х = 4, у = 0.
2. Обчисліть площу земельної ділянки , яка мас форму криволінійної трапеції, обмеженої лініями у=х²-2х+2, х=-1, х=2, у=0.

3. Квітами засіяно ділянку, яка мас форму криволінійної трапеції, обмеженої лініями у=5х-х²-4, у = 0. Знайдіть її площу.

4. Обчисліть площу лапи культиватора, форму якої можна описати лініями у=х² х=3, у=0.
5. Сад займає ділянку, що має форму криволінійної трапеції, обмеженої лініями

у = х² + 3. у= х + 1, х = 1, х= 3. Знайдіть площу саду.

6. Яка площа лемеша плуга, якщо його форму можна описати лініями

у₁= х² + 4,  у₂= х,  х₁= 1, х₂=2?

7. Поперечний переріз провідника мас форму, яку можна описати перетином ліній у₁ = х²,  у₂ = 1- х².                  Обчисліть              площу              цього перерізу.
8. Жолоб, по якому тече вода, мас форму криволінійної трапеції, обмеженої лініями у= 1/3 х², у = 3. Обчисліть площу поперечного перерізу жолоба.
9. Шматок тканини мас форму криволінійної трапеції, обмеженої лініями

у = х² + 6х+ 12,   у = 2 х.  Обчисліть площу шматка тканини.

10. Лист жерсті мас форму криволінійної трапеції, обмеженої лініями у = х² + 3, у = 1. х = 1, х=3. Обчисліть площу цього листа.
11. Форму китобійного гарпуна можна описати лініями: у₁ = 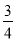х² , у₂ = 0,

у₃ = - х- , у₄ =-; у₅ = х² - 1,5, у₆= - 1,5; х = 2. Обчисліть площу бічної' поверхні гарпуна..

12.        Петля  гістерезисну феромагнетика (намагнічування-рочмагнічування) описується функціями у₁ = х³+ х² – 4,  у₂ = х³ - х² + 4. Знайдіть площу ції фігури.

Застосування інтеграла

1.   Обчисліть об'єм тіла, утвореного обертанням фігури, обмеженої однією півхвилею синусоїди у = sinх і відрізом 0 x   навколо осі ОХ.
2.   Обчислить об'єм клина, відрізаного від циліндра площиною, що проходить через діаметр основи і нахилена до основи під кутом α. Радіус основи циліндра дорівнює R.
3.   Знайдіть роботу, яку потрібно виконати, щоб стиснути пружину на 20 см. якою відомо, що сила пропорційна стиску пружини, а жорсткість її дорівнює 29,4 Н/см.
4.   Пружина терезів під дією сили 1 Н розтягується на 1 см. Яку роботу треба виконати, щоб розтягти її на 4 см ?
5.   Сила пружності пружини динамометра, розтягнутої на 5 см, дорівнює 0,2 Н. Яку робочу треба виконати, щоб розтягти її на 6 см ?
6.   Обчисліть роботу, яку треба виконати, щоб викачати воду з ями завглибшки 4 м, що мас квадратний переріз зі стороною 2 м. Густина води р = 10³ кг/м³.

7.Обчисліть масу металевого стержня з густиною р(х) і завдовжки n, де n [0,4].

8. Сила стуму I в провіднику змінюється з часом t за законом I= 4 + 2 t (А). Який заряд пройде через провідник за час з другої до шостої секунди ?

9.  Вхід до ангара має форму лапки синусоїди. Скільки треба фарби для фарбування дверей ангара, якщо його висота 10 м. а на 1 м²  витрачається 0,3 л фарби ?

10. Знайдіть кількість теплоти, що виділяється під час проходження електричного струму через провідник через 5 с після ввімкнення струму, якщо опір задано функцією від часу

R= 5 t²- 2 (Ом), а сила струму І= 10 А.

11. Котел, що має форму півсфери радіуса R, заповнено водою. Яку роботу треба виконати, щоб викачати воду з цього котла ?

11. Знайдіть кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила струму змінюється за законом I (t) = (4 t + 1) (А).
12. Залежність кутової швидкості лопастей гелікоптера від часу можна описати формулою

      W= 2 + 2 t (рад/с). Скільки обертів зроблять лопасті гелікоптера за 20 с після запуску

двигуна ?

13. Знайдіть роботу, яку викопують сили гравітаційного поля Землі, якщо тіло масою 1 кг падає на її поверхню з висоти, що дорівнює радіусу Землі

(R_З = 6.37 .10⁶ м, т_З = 5.98 ·10²⁴  кг).

14. Вертикальна циліндрична цистерна діаметра 4 м заввишки 6 м заповнена водою. Визначте час. за який може витекти вся вода через круглий отвір діаметра 1/6 м, що розміщений у дні.
15. Знайдіть густину гриба, шляпка якого має форму тіла, яке утворюється в результаті обертання частини синусоїди навколо горизонтальної осі, а ніжка - циліндричне тіло заввишки 2 см і радіуса 0,8 см. маса гриба 0,03 кг.

Література 1. Бевз Г.П. Алгебра (алгебра і початки аналізу):підруч. для 11 кл. загальноосвіт. навч. закл.:рівень стандарту, академ. рівень, проф. рівень / Г.П. Бевз, В.Г. Бевз, Н.Г. Владімірова – К.: Освіта, 2019.-400 с

2. . Мерзляк А.Г. Алгебра і початки аналізу: підруч. для 11 кл. загальноосвіт. навч. закладів: академ. рівень, проф.. рівень / А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2019-331 с.

3. Навчальна програма з математики для учнів 10-11 класів загальноосвітніх навчальних закладів (для класів з рівнем стандарту.

4. Соколенко Л.О. Прикладна спрямованість шкільного курсу алгебри і початків аналізу: Навч. посібник. -Чернігів:Сіверянська думка,2002.-128с. 11.

5. Соколенко Л.О., Філон Л.Г., Швець В.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу: практикум. Навчальний посібник. –Київ: НПУ імені М.П. Драгоманова, 2010.-128с.

6. Cоколенко Л.О. Збірник прикладних задач з алгебри і початків аналізу: Навч.- метод. посібник для вчителів і учнів 10-11 кл. середн. шк., ліцеїв та гімназій фізико-математичного спрямування. – Київ: ”Тираж”, 1997.-127с. 13. 7. 7. Соколенко Л.О. Прикладні аспекти математики: інтеграл та його застосування в класах природничого профілю // Вісник ЧДПУ імені Т.Г. Шевченка. Серія: Педагогічні науки,- 2006, Вип. 42, -С. 74-77.

8. Соколенко Л.О., Швець В.О. Різні типи прикладних задач, що призначені для вивчення похідної та її застосувань у курсі алгебри і початків аналізу // Математика в рідній школі, - 2014, №9, - С.2-10.

9. Ткач Ю.М. Математика. Задачі економічного змісту в математиці: Навчально-методичний посібник / Ю.М. Ткач. – Х.: Вид-во ”Ранок”, 2011.-176с.

10. Шкіль М.І. та ін. Алгебра і початки аналізу: Підруч. для 11 кл. загальноосвіт. навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. -К.: Зодіак-ЕКО, 2002.-384 с.

Різні типи прикладних задач, що призначені для вивчення інтеграла та його застосувань у курсі алгебри і початків аналізу