Зведення дробів до НСЗ. Порівняння дробів
Тема. Зведення дробів до НСЗ. Порівняння дробів
Мета: доповнити знання учнів правилом порівняння дробів з різними знаменниками; систематизувати вивчений з приводу порівняння дробів матеріал, завершити формування вмінь знаходити НСЗ і зводити дроби до найменшого спільного знаменника.
Тип уроку: засвоєння та систематизація знань.
Хід уроку
I. Перевірка домашнього завдання і актуалізація опорних знань
Ця тема є основою теми «Додавання і віднімання дробів», тому треба ретельно перевірити виконання домашнього завдання учнями, щоб своєчасно виправити можливі помилки.
Роботу можна виконати в ігровій формі «Знайди помилку».
Учитель заздалегідь записує на відкидній дошці розв'язання домашніх вправ, «припустившись» кількох найтиповіших помилок (неправильно знайдено спільний знаменник, неправильно обчислений додатковий множник; не виконано множення чисельника на додатковий множник тощо).
Завдання учнів при цьому — звірити свої розв'язання з тим, що вони бачать на дошці, та знайти помилки й пояснити їх причину.
Після такої роботи можна ще раз повторити основні поняття, терміни та алгоритми, що їх було вивчено на попередньому уроці й перейти до наступного етапу уроку.
II. Завершення формування нових знань, систематизація раніше набутих знань
Завдання 1. Порівняйте дріб ![]() з дробом: а)
з дробом: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Якими правилами ви скористалися, щоб виконати це завдання?
Завдання 2. Порівняйте дріб ![]() з дробом: а)
з дробом: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Чи зможете ви виконати це завдання, скориставшись яким-небудь з правил, використаних у завданні 1?
Після обговорення проблеми деякі учні можуть рамі запропонувати такий шлях виконання або звести дроби до спільного знаменника або (можуть бути й такі) до спільного чисельника. Вчителю слід наголосити на тому, що зведення дробів до спільного знаменника є традиційним способом порівняння дробів з різними знаменниками, і обов'язково наголосити на тому, що це правило не відміняє, а доповнює вивчене раніше.
Результатом усіх міркувань може стати конспект 10.
|
Конспект 10 Порівняння звичайних дробів
а) з однаковими знаменниками:
б) з однаковими чисельниками: в) правильного з неправильним: п < н;
г) з різними знаменниками: щоб порівняти
Приклад: а)
в)
г) |
* Якщо є учні, що цікавляться математикою, можна ознайомитись з іншими способами порівняння звичайних дробів (наприклад, 1) за доповненням дробів до 1: ![]() і
і ![]() мають доповнення до 1:
мають доповнення до 1: ![]() і
і ![]() відповідно, отже,
відповідно, отже, ![]() (див. приклад б), тому
(див. приклад б), тому ![]() - згідно із властивістю віднімання;
- згідно із властивістю віднімання;
2) порівняння з половиною: ![]() , бо
, бо ![]() ,
, ![]() іт. ін.)
іт. ін.)
III. Формування вмінь
На уроці, в основному, продовжується робота з формування вмінь знаходити НСЗ для кількох звичайних дробів і зводити дані дроби до НСЗ за алгоритмом. Тому доцільним буде розв'язати такі вправи:
- Зведіть до найменшого спільного знаменника дроби:
а) ![]() ,
, ![]() і
і ![]() ; б)
; б) ![]() ,
, ![]() і
і ![]() ; в)
; в) ![]() ,
, ![]() ,
, ![]() і
і ![]() .
.
-
Порівняйте дроби: а)
 і
і 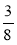 ; б)
; б) 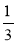 і
і 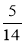 ; в)
; в) 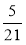 і
і 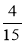 ; г)
; г) 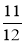 і
і 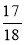 .
.
-
Розмістіть у порядку зростання дроби:
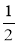 ;
; 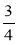 ;
; 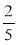 ;
;  ;
; 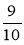 ;
; 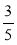 .
.
-
Розмістіть дроби в порядку спадання:
 ;
; 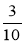 ;
; 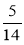 ;
; 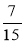 ;
; 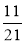 ;
; 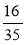 .
.
Додатково можна запропонувати учням такі завдання:
-
Дано три цифри: 2; 5; 7. З них можна скласти правильні дроби, наприклад:
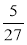 і т. д. Складіть з цих цифр найбільший та найменший правильний дріб.
і т. д. Складіть з цих цифр найбільший та найменший правильний дріб.
-
Скоротіть: а)
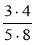 ; б)
; б) 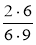 ; в)
; в) 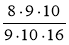 ; г)
; г) 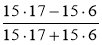 ; д)
; д) 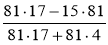 .
.
-
Виконайте дії і скоротіть результат:
а)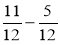 ; б)
; б) 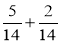 ; в)
; в)  ; г)
; г) 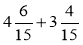 .
.
IV. Підсумки уроку
Оберіть найзручніший спосіб порівняти числа:
![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() .
.
V. Домашнє завдання
-
Порівняйте дроби: а)
 і
і 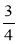 ; б)
; б) 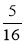 і
і 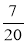 ; в)
; в)  і
і 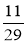 ; г)
; г) 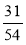 і
і 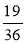 .
.
-
Зведіть до найменшого спільного знаменника дроби:
а)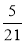 ,
, 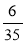 і
і 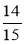 ; б)
; б)  ,
, 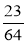 і
і 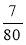 ; в)
; в) 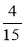 ,
, 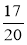 ,
, 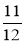 і
і 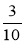 .
.
-
Розмістіть дроби в порядку зростання:
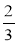 ;
; 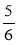 ;
; 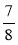 ;
; 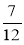 ;
; 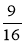 ;
; 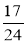 .
.
-
Виконайте дії: а)
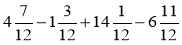 ; б)
; б) 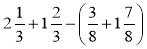 .
.


про публікацію авторської розробки
Додати розробку
