Діофантові рівняння.
1
.
Автор - упорядник:
Михальчук Оксана Олександрівна, вчитель, Ізюмська загальноосвітня школа І-ІІІ ступенів
№ 11 Ізюмської міської ради Харківської області, спеціаліст вищої категорії.
Діофантові рівняння.
Дана робота – спроба розробити серію факультативних занять із математики для учнів 6-9 класів за темою « Діофантові рівняння», які містять різнорівневі завдання з теми і ознайомлять дітей із основними способами розв’язання таких рівнянь . Задачі, які зводяться до розв’язання діофантових рівнянь, часто зустрічаються на олімпіадах різних рівнів і є однією з найулюбленіших тем у теоретико-числових дослідженнях математиків. Розв’язання діофантових рівнянь сприяє розвитку теоретичного та логічного мислення школярів.
Робота призначена для вчителів математики середніх і старших класів.
Зміст.![]()
Вступ…………………………….…………………………………………………..4
- Математичні основи розв’язування діофантових рівнянь………………….…6
1.1.Рівняння першого степеня з двома невідомими……………………………….6
1.2. Рівняння другого степеня………………………………………………………7
1.2.1. Приклад розв’язування рівняння другого степеня з трьома невідомими…7
1.2.2. Рівняння другого степеня з двома невідомими……………………………..9
1.3. Рівняння з двома невідомими степеня вище другого……………………...…9
2. Методика підготовки учнів до розв’язання олімпіадних задач, пов’язаних із діофантовими рівняннями………………………………..…………………..10
2.1. Принципи відбору теоретичного матеріалу………………………………..10
2.2. Найпростіші методи розв’язування діофантових рівнянь………………….11
3. Додатки…………………………………………………………………………...11
3.1. Розробки факультативних занять за темою «Діофантові рівняння»….…..11
3.1.1. Заняття № 1……………………………………………………………….….11
3.1.2. Заняття № 2…………………………………………………………………..14
3.1.3. Заняття № 3……………………………………………………………….….18
3.1.4. Заняття № 4………………………………………………………………..…20
3.1.5. Заняття № 5………………………………………………………………....24
3.1.6. Заняття № 6………………………………………………………………….29
Висновки……………………………………………………………………………33
Література………………………………………………………………………….34
Вступ.
Теорія чисел вивчає насамперед арифметичні властивості чисел натурального ряду, іншими словами, цілих додатних чисел, і належить до старовинних розділів математики. Однією із центральних задач так званої аналітичної теорії чисел є задача про розподіл простих чисел у натуральному ряду. Простим числом називається будь – яке ціле додатне число, більше одиниці, що поділяється тільки на себе і одиницю. Задача про розподіл простих чисел у натуральному ряду полягає у вивченні правильності поведінки кількості простих чисел, менших деякого числа ![]() , при великих значеннях
, при великих значеннях ![]() . Перший результат у цьому напрямку ми знаходимо ще у Евкліда (
. Перший результат у цьому напрямку ми знаходимо ще у Евкліда (![]() ст. до н.е.), саме доведення нескінченності ряду простих чисел; другий результат після Евкліда був отриманий видатним російським математиком П.Л.Чебишевим у другій половині
ст. до н.е.), саме доведення нескінченності ряду простих чисел; другий результат після Евкліда був отриманий видатним російським математиком П.Л.Чебишевим у другій половині![]() ст. Інша основна задача теорії чисел - це задача про подачу цілих чисел у вигляді суми цілих чисел певного типу, наприклад, проблема подачі непарних чисел у вигляді суми трьох простих чисел, яка була розв’язана сучасним представником теорії чисел - радянським математиком І.М.Віноградовим .
ст. Інша основна задача теорії чисел - це задача про подачу цілих чисел у вигляді суми цілих чисел певного типу, наприклад, проблема подачі непарних чисел у вигляді суми трьох простих чисел, яка була розв’язана сучасним представником теорії чисел - радянським математиком І.М.Віноградовим .
Дана робота присвячена одному із найбільш цікавих розділів теорії чисел, а саме - розв’язуванню рівнянь у цілих числах або діофантових рівнянь.
Розв’язок у цілих числах алгебраїчних рівнянь з цілими коефіцієнтами більш ніж із одним невідомим являє собою одну із складніших проблем теорії чисел. Цими задачами багато займались самі видатні математики давнини: грецький математик Піфагор (![]() ст. до н.е. ); кращі математики більш близької до нас доби –П.Ферма (
ст. до н.е. ); кращі математики більш близької до нас доби –П.Ферма (![]() ст.), Л.Ейлер (
ст.), Л.Ейлер (![]() ст. ), Ж.Л.Лагранж (
ст. ), Ж.Л.Лагранж ( ![]() ст.) та інші.
ст.) та інші.
Одним із математиків, що займались цією проблемою, був давньогрецький математик Діофант Олександрійський, праці якого мали велике значення для алгебри та теорії чисел. До нашого часу не з’ясовані ні рік народження, ні дата смерті Діофанта ; вважають, що він жив у ![]() ст. н.е. В одному із давніх рукописних збірників задач у віршах життя Діофанта описується у вигляді наступної алгебраїчної загадки, що являє собою надпис на його могилі:
ст. н.е. В одному із давніх рукописних збірників задач у віршах життя Діофанта описується у вигляді наступної алгебраїчної загадки, що являє собою надпис на його могилі:
Прах Диофанта гробница покоит; дивись ей – камень,
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Задача – загадка зводиться до складання і розв’язування рівняння:
![]() ,
,
звідки ![]() - ось скільки років жив Діофант.
- ось скільки років жив Діофант.
Із робіт Діофанта найважливішою є „Арифметика”, з 13 книг якої тільки 6 збереглися до наших днів. Ці книги були відкриті у Венеції у 1463 р. Регіомонтаном, котрий у зв’язку з цим писав, що у праці Діофанта зосереджено „увесь колір арифметики, мистецтва невідомої”.
У збережених книгах Діофанта міститься 189 задач із розв’язанням. У першій книзі викладені задачі, що зводяться до визначених рівнянь першого та другого степенів. Інші п’ять книг містять в основному невизначені рівняння. У цих книгах ще нема систематичної теорії невизначених рівнянь, методи розв’язування змінюються від випадку до випадку. Діофант задовольняється будь – яким одним розв’язком, цілим або дробовим, аби він було додатнім.
Методи розв’язання невизначених рівнянь складають основний вклад Діофанта у математику. Відомо, що у символіці Діофанта був один тільки знак для невідомого. Розв’язуючи невизначене рівняння, він використовував у якості декількох невідомих довільні числа, замість яких можна було взяти і будь – які інші, що і зберігало характер загальності його розв’язку .
Не дивлячись на зусилля багатьох поколінь видатних математиків, у цій області відсутні загальні методи. Проблема розв’язування рівнянь у цілих числах вирішена до кінця тільки для рівнянь другого степеня з двома невідомими. Слід зазначити, що для рівнянь будь – якого степеня з одним невідомим вона не представляє суттєвого інтересу, бо ця задача може бути розв’язана за допомогою кінцевого числа спроб. Для рівнянь вищих степенів із двома та більше невідомими дуже складна не тільки задача знаходження усіх розв’язків у цілих числах, але і більш проста задача встановлення існування кінцевої або нескінченної множини таких розв’язків.
Розв’язання рівнянь у цілих числах має не тільки теоретичний інтерес. Такі рівняння іноді зустрічаються у фізиці та практиці людини. Крім того діофантові рівняння і задачі, які зводяться до діофантових рівнянь досить часто зустрічаються в завданнях математичних олімпіад різних рівнів . Оскільки діофантові рівняння не вивчаються в основному курсі математики в школі, доцільно організовувати знайомство учнів з основними ідеями, пов’язаними з діофантовими рівняннями, на факультативних заняттях.
Тому, метою роботи було розробити серію факультативних занять, на яких учні зможуть оволодіти методами розв’язування олімпіадних задач, пов’язаних із діофантовими рівняннями. Для досягнення цієї мети було поставлено такі завдання:
- проаналізувати математичні основи теорії діофантових рівнянь і відібрати теоретичний матеріал, з яким доцільно познайомити учнів;
- виділити основні методи розв’язування задач, пов’язаних із діофантовими рівняннями;
- підібрати різнорівневу систему завдань для відпрацювання кожного методу;
- розробити систему занять по ознайомленню учнів із завданнями, які зводяться до діофантових рівнянь і розробити методичні рекомендації по проведенню цих занять.
1. Математичні основи розв’язування діофантових рівнянь.
1.1. Рівняння першого степеня з двома невідомими.
Спочатку розглянемо рівняння першого степеня з одним невідомим
![]() (1)
(1)
Нехай коефіцієнти рівняння ![]() та
та ![]() – цілі числа. Зрозуміло, що розв’язок цього рівняння
– цілі числа. Зрозуміло, що розв’язок цього рівняння ![]() буде цілим числом тільки в тому випадку, коли
буде цілим числом тільки в тому випадку, коли ![]() буде ділитись на
буде ділитись на ![]() без залишку. Таким чином, рівняння (1) не завжди має розв’язки у цілих числах.
без залишку. Таким чином, рівняння (1) не завжди має розв’язки у цілих числах.
Так само і рівняння, степінь яких вище одиниці. Але питання про знаходження цілих коренів рівняння n-го степеня з цілими коефіцієнтами
![]() (2)
(2)
розв’язується легко.
Дійсно, нехай ![]() – цілий корінь цього рівняння.
– цілий корінь цього рівняння.
Тоді ![]() ,
, ![]() .
.
З останньої рівності видно , що а0 ділиться на а без залишку ; отже, кожний цілий корінь рівняння (2) є дільником вільного вільного члена рівняння. Для знаходження цілих розв’язків рівняння треба вибрати ті з дільників ![]() , котрі при підстановці у рівняння перетворюють його у тотожність.
, котрі при підстановці у рівняння перетворюють його у тотожність.
Значно більший інтерес являє розв’язання у цілих числах рівнянь з багатьма невідомими.
Отже, розглянемо рівняння першого степеня з двома невідомими
![]() , (3)
, (3)
де ![]() і
і ![]() - цілі числа, відмінні від нуля, а
- цілі числа, відмінні від нуля, а ![]() - довільне ціле. Будемо вважати, що коефіцієнти
- довільне ціле. Будемо вважати, що коефіцієнти ![]() та
та ![]() не мають спільних дільників, крім одиниці. Дійсно, якщо найбільший спільний дільник цих коефіцієнтів
не мають спільних дільників, крім одиниці. Дійсно, якщо найбільший спільний дільник цих коефіцієнтів ![]() відмінний від одиниці, то справджуються рівності
відмінний від одиниці, то справджуються рівності ![]() ,
, ![]() ; рівняння (3) приймає вигляд
; рівняння (3) приймає вигляд ![]() і має мати цілі розв’язки тільки в тому випадку, коли
і має мати цілі розв’язки тільки в тому випадку, коли ![]() ділиться на
ділиться на ![]() . Таким чином, у випадку
. Таким чином, у випадку ![]() усі коефіцієнти рівняння (3) повинні ділитись на
усі коефіцієнти рівняння (3) повинні ділитись на ![]() без залишку, і, скоротивши (3) на
без залишку, і, скоротивши (3) на ![]() , прийдемо до рівняння
, прийдемо до рівняння ![]() ,
,![]() , коефіцієнти якого
, коефіцієнти якого ![]() та
та ![]() взаємно прості.
взаємно прості.
Розглянемо спочатку випадок, коли ![]() . Рівняння (3) матиме вигляд:
. Рівняння (3) матиме вигляд:
![]() (3’).
(3’).
Розв’язуючи це рівняння відносно ![]() , отримаємо
, отримаємо ![]() . Зрозуміло, що
. Зрозуміло, що ![]() буде приймати цілі значення лише в тому випадку, коли
буде приймати цілі значення лише в тому випадку, коли ![]() ділиться на
ділиться на ![]() без остачі. Але будь-яке ціле
без остачі. Але будь-яке ціле ![]() , що кратне
, що кратне ![]() , можна записати у вигляді:
, можна записати у вигляді: ![]() , де
, де ![]() приймає довільні цілі значення
приймає довільні цілі значення ![]() . Підставимо це значення
. Підставимо це значення ![]() у попереднє рівняння , тоді
у попереднє рівняння , тоді ![]() , і ми отримаємо формули, що містять всі цілі розв’язки рівняння (3’) :
, і ми отримаємо формули, що містять всі цілі розв’язки рівняння (3’) :![]()
![]() .
.
Перейдемо до випадку ![]() . Для знаходження всіх цілих розв’язків рівняння (3) достатньо знайти будь-який один його розв’язок , тобто знайти такі цілі числа
. Для знаходження всіх цілих розв’язків рівняння (3) достатньо знайти будь-який один його розв’язок , тобто знайти такі цілі числа ![]() , для яких
, для яких ![]() .
.
Теорема I. (без доведення) Нехай ![]() і
і ![]() взаємно прості і
взаємно прості і ![]() - будь-який розв’язок рівняння
- будь-який розв’язок рівняння ![]() (3). Тоді формули
(3). Тоді формули ![]() (4) при
(4) при ![]() дають усі розв’язки рівняння (3).
дають усі розв’язки рівняння (3).
1.2.Рівняння другого степеня.
1.2.1. Приклад розв’язування рівняння другого степеня з трьома невідомими.
Приклад. Розглянемо рівняння другого степеня з трьома невідомими:
![]() (5)
(5)
Геометрично розв’язок цього рівняння у цілих числах можна подати як знаходження всіх піфагорових трикутників, тобто прямокутних трикутників, у яких катети ![]() і гіпотенуза
і гіпотенуза ![]() виражені цілими числами.
виражені цілими числами.
Позначимо через ![]() найбільший спільний дільник чисел
найбільший спільний дільник чисел ![]() та
та ![]() :
:![]() . Тоді
. Тоді ![]() ,
,![]() і рівняння (5) прийме вигляд
і рівняння (5) прийме вигляд
![]()
![]()
Звідси випливає, що ![]() ділиться на
ділиться на ![]() і, значить
і, значить ![]() кратне
кратне ![]() :
: ![]()
Тепер рівняння (5) можна записати у вигляді
![]()
![]()
Скоротивши на ![]() , одержимо
, одержимо
![]() =
=![]() .
.
Ми прийшли до рівняння того ж виду, що і початкове, причому тепер величини ![]() не мають спільних дільників, крім 1. Таким чином, при розв’язанні рівняння (5) можна обмежитись випадком, коли
не мають спільних дільників, крім 1. Таким чином, при розв’язанні рівняння (5) можна обмежитись випадком, коли ![]() взаємно прості. Отже, нехай НСД
взаємно прості. Отже, нехай НСД![]() . Тоді, хоча б одна з величин
. Тоді, хоча б одна з величин ![]() та
та ![]() (наприклад,
(наприклад, ![]() ) буде непарною.
) буде непарною.
Перенесемо ![]() у праву частину рівняння (5), отримаємо
у праву частину рівняння (5), отримаємо
![]() ;
; ![]() (6)
(6)
Позначимо через ![]() найбільший спільний дільник виразів
найбільший спільний дільник виразів ![]() та
та ![]() , тоді
, тоді
![]() ,
, ![]() , (7)
, (7)
де ![]() і
і ![]() взаємно прості.
взаємно прості.
Підставляючи в (6) значення ![]() та
та ![]() , отримаємо
, отримаємо ![]() . Так як числа
. Так як числа ![]() і
і ![]() не мають спільних дільників, то одержана рівність можлива лише у випадку , коли
не мають спільних дільників, то одержана рівність можлива лише у випадку , коли ![]() і
і ![]() будуть повними квадратами:
будуть повними квадратами: ![]() ,
,![]()
Але тоді
![]() і тоді
і тоді ![]() (8)
(8)
Знайдемо тепер ![]() та
та ![]() із рівностей (7) . Додавання цих рівностей дає
із рівностей (7) . Додавання цих рівностей дає
![]()
![]()
![]() ;
; ![]() (9)
(9)
Віднімаючи другу рівність (7) від першої отримаємо
![]()
![]()
![]() ;
; ![]() (10)
(10)
В силу непарності ![]() із (15) маємо, що
із (15) маємо, що ![]() і
і ![]() також непарні. Більш того,
також непарні. Більш того, ![]() так як інакше з рівностей
так як інакше з рівностей ![]() та
та ![]() випливало б, що величини
випливало б, що величини ![]() та
та ![]() мають спільний дільник
мають спільний дільник ![]() , що суперечить припущенню про їх взаємну простоту. Числа
, що суперечить припущенню про їх взаємну простоту. Числа ![]() та
та ![]() пов’язані із взаємно простими числами та рівностями і в силу цього самі взаємно прості;
пов’язані із взаємно простими числами та рівностями і в силу цього самі взаємно прості;![]() ,бо
,бо ![]() ,що зрозуміло із рівностей (7).
,що зрозуміло із рівностей (7).
Підставляючи у рівності (8) – (10) ![]() ,отримаємо формули:
,отримаємо формули:
![]() ,
, ![]() ,
, ![]() , (11)
, (11)
що дають при непарних взаємно простих ![]() та
та ![]() усі вільні від спільних дільників трійки цілих додатних чисел
усі вільні від спільних дільників трійки цілих додатних чисел ![]() , що задовольняють рівнянню (5) . Простою підстановкою
, що задовольняють рівнянню (5) . Простою підстановкою ![]() та
та ![]() у рівняння (5) легко перевірити, що при будь- яких
у рівняння (5) легко перевірити, що при будь- яких ![]() та
та ![]() числа (11) задовольняють цьому рівнянню.
числа (11) задовольняють цьому рівнянню.
Звідси випливають рівності, які часто зустрічаються:
![]() (
(![]() ),
),
![]() (
(![]() ),
),
![]() (
(![]() ).
).
Як вже було сказано, формули (11) дають тільки ті розв’язки рівняння ![]() , в яких числа
, в яких числа![]() та
та ![]() не мають спільних дільників. Всі інші цілі додатні розв’язки цього рівняння можна отримати, якщо помножити розв’язки, що містяться у формулах (11), на довільний спільний множник
не мають спільних дільників. Всі інші цілі додатні розв’язки цього рівняння можна отримати, якщо помножити розв’язки, що містяться у формулах (11), на довільний спільний множник ![]() .
.
Тим самим шляхом , яким ми одержали усі розв’язки рівняння (5), можуть бути одержані і всі розв’язки інших рівнянь того ж типу.
1.2.2. Рівняння другого степеня з двома невідомими.
Теорема II(без доведення). Будь – який розв’язок рівняння ![]() (12) при додатному
(12) при додатному ![]() та ірраціональному
та ірраціональному![]() має вигляд
має вигляд
![]() , де
, де
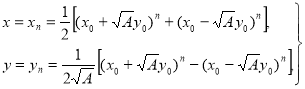 (13)
(13)
а ![]() - найменший розв’язок.
- найменший розв’язок.
Наприклад, найменшим розв’язком рівняння ![]() буде
буде ![]() ,
, ![]() , усі розв’язки цього рівняння будуть міститись у формулах:
, усі розв’язки цього рівняння будуть міститись у формулах:
![]() ,
,
![]() ,
,
Звідки при ![]() , ми отримуємо розв’язки:
, ми отримуємо розв’язки: ![]() .
.
Відмітимо, що числа ![]() та
та ![]() із зростанням n зростають із швидкістю геометричної прогресії із знаменником
із зростанням n зростають із швидкістю геометричної прогресії із знаменником ![]() ,так як внаслідок рівності (
,так як внаслідок рівності (![]() )(
)(![]() )=1 ми можемо стверджувати, що 0<
)=1 ми можемо стверджувати, що 0<![]() <
<![]() <1 і тому
<1 і тому
(![]() )
)![]() завжди прямує до 0 із зростанням n.
завжди прямує до 0 із зростанням n.
ТЕОРЕМА III(без доведення). При будь-якому цілому додатному А та ірраціональному ![]() рівняння (12)
рівняння (12) ![]() має розв`язок
має розв`язок ![]() ,
, ![]() ,
, ![]() .
.
У випадку другого степеня пари цілих чисел, які можуть бути розв’язками рівняння, зустрічаються значно рідше, ніж пари цілих чисел, що можуть бути розв’язками рівняння першого степеня.
1.3. Рівняння з двома невідомими степеня вище другого.
a0xn + a1xn-1y + a2xn-2y2 + … + anyn , (14)
де n – ціле число, більше за 2, і всі числа a0, a1, a2, …, an, c – цілі числа.
Рівняння з двома невідомими степеня вище другого майже завжди можуть мати тільки кінцеву кількість розв’язків у цілих числах х та у.
- .Алгебраїчні рівняння вищих порядків із трьома невідомими.
Якщо для рівнянь з двома невідомими ми можемо дати відповідь на питання про існування кінцевої або нескінченої кількості розв’язків у цілих числах, то для рівнянь вищих порядків з кількістю невідомих більше ніж два дати відповідь на це питання ми можемо лише для деяких окремих класів рівнянь. Видатний французький математик П’єр Ферма висловив твердження, що рівняння
xn + yn = zn (15)
при цілому n ![]() 2 не має розв’язків у цілих додатніх числах x, y та z (випадок xyz = 0 виключається додатністю x, y, z.
2 не має розв’язків у цілих додатніх числах x, y та z (випадок xyz = 0 виключається додатністю x, y, z.
Таким чином, загальна теорія розв’язування рівнянь у цілих числах повністю розроблена тільки для рівнянь першого та другого степенів із двома невідомими. Для рівнянь вищих степенів з двома та більш невідомими дуже складна не тільки задача знаходження усіх розв’язків у цілих числах, але і більш проста задача встановлення існування кінцевої або нескінченної множини таких розв’язків.
На факультативних заняттях доцільно познайомити учнів з найпростішими випадками діофантових рівнянь та методами їх розв’язування, із загальними методами розв’язування лінійних діофантових рівнянь.
2. Методика підготовки учнів до розв’язання олімпіадних задач, пов’язаних із діофантовими рівняннями.
2.1. Принципи відбору теоретичного матеріалу:
- Принцип науковості та посильної складності, який передбачає відповідність запропонованого матеріалу рівню сучасної науки, збереження наукової системи у певній послідовності, а також міжпредметних зв’язків разом із врахуванням у процесі навчання вікових та індивідуальних особливостей учнів.
- Принцип розвитку теоретичного мислення. Передбачає розвиток теоретичного та логічного мислення учнів.
- Принцип систематичності. Реалізується за допомогою цільової і логічної систематизації, які повинні допомогти учням оволодіти системними знаннями.
- Принцип переходу від навчання до самонавчання і розвиток пізнавальних сил учнів. Сутність цього принципу полягає у пристосуванні навчання до змісту та рівня знань та вмінь, навичок кожного учня з метою виховання творчого підходу при вивченні кожного питання, вміння критично оцінювати результати своєї роботи, здатність до самоконтролю та самонавчання.
- Практична важливість і зв’язок матеріалу із досвідом учнів. Передбачає можливість подання матеріалу на основі вивченого учнями раніше та можливість запропонувати учням нові нестандартні методи розв’язання математичних задач з метою активізувати процес навчання.
- Перспективне значення матеріалу. Передбачає можливість використовувати його у подальшій учбовій діяльності.
2.2. Найпростіші методи розв’язування діофантових рівнянь.
- Метод повного перебору.
- Використання властивостей подільності.
- Виділення цілої частини.
3. Додатки.
3.1. Розробка факультативних занять за темою «Діофантові рівняння».
3.1.1. Заняття № 1.
Тема уроку: Діофант та діофантові рівняння. Розв’язування діофантових рівнянь методом повного перебору.
Тип уроку : Засвоєння нових знань, вмінь
Мета уроку: - ознайомити учнів із поняттям діофантового рівняння;
- сформувати вміння розв’язувати діофантові рівняння,
використовуючи метод повного перебору.
Хід уроку:
Перший етап даного уроку треба присвятити ознайомленню учнів із питаннями історії діофантових рівнянь. Для цього доцільно запропонувати учням самостійно підготувати реферат за темою «Про Діофанта та діофантові рівняння».
Означення: Діофантові рівняння – алгебраїчні рівняння або системи рівнянь із раціональними коефіцієнтами, розв’язки яких знаходять у цілих або раціональних числах. Зазвичай припускають, що діофантові рівняння мають кількість невідомих більшу, ніж кількість рівнянь, у зв’язку з цим вони також називаються невизначеними рівняннями.
Найпростішими методами розв’язування діофантових рівнянь є:
- метод повного перебору;
- метод, пов’язаний із використанням властивостей подільності чисел;
- метод, пов’язаний із виділенням цілої частини або метод розсіювання.
Найбільш простим методом розв’язання діофантових рівнянь є метод повного перебору, тому заняття слід почати із розгляду декількох рівнянь, що розв’язуються за допомогою цього методу.
Задача 1: знайти двозначне число, яке дорівнює подвоєному добутку його цифр.
Розв’язання:
Позначимо шукане двозначне число через ![]() (риска над значенням числа, що записане за допомогою цифр
(риска над значенням числа, що записане за допомогою цифр ![]() та
та ![]() , ставиться для того, щоб відрізнити цей запис від запису добутку
, ставиться для того, щоб відрізнити цей запис від запису добутку ![]() ). Так як число
). Так як число ![]() містить
містить ![]() десятків і
десятків і ![]() одиниць, то:
одиниць, то: ![]() .
.
За умовою задачі : ![]() або
або ![]() .
.
Звідки ![]() .
.
Враховуючи, що ![]() та
та ![]() - цифри
- цифри ![]() , шуканий результат можна отримати за допомогою повного перебору усіх можливих значень
, шуканий результат можна отримати за допомогою повного перебору усіх можливих значень ![]() , тобто у останню рівність треба просто послідовно підставити замість
, тобто у останню рівність треба просто послідовно підставити замість ![]() значення
значення ![]() . Виконавши підстанови, впевнюємося, що лише одне значення
. Виконавши підстанови, впевнюємося, що лише одне значення ![]() задовольняє рівність. В цьому випадку
задовольняє рівність. В цьому випадку ![]() , тобто:
, тобто:
![]()
![]() .
.
Відповідь : шукане число 36.
Отже, метод повного перебору полягає в наступному: у рівняння треба підставити послідовно усі можливі значення невідомих і вибрати ті, що дають цілі розв’язки рівняння.
Після розгляду задачі 1 слід розглянути більш складну задачу, пов’язану із повним перебором.
Задача 2: Знайти усі двозначні числа, кожне з яких на 9 більше суми квадратів його цифр.
Розв’язання: Позначимо шукане двозначне число через ![]() . Тоді за умовою задачі:
. Тоді за умовою задачі:
![]() або
або ![]() (
(![]() ,
, ![]() - цифри).
- цифри).
Перепишемо це рівняння у вигляді:
![]()
Вважаємо, що це квадратне рівняння відносно ![]() . Воно буде мати розв’язок тільки при невід’ємному дискримінанті:
. Воно буде мати розв’язок тільки при невід’ємному дискримінанті:
![]()
![]() при умові
при умові
![]()
Розв’язуючи цю нерівність, отримуємо:
![]()
Цій умові задовольняють лише цифри ![]() .
.
Цю нерівність розв’язувати зовсім необов’язково, можна просто перевірити, що із всіх цифр цій нерівності задовольняють лише цифри ![]() .
.
Розглянемо, чи має це рівняння розв’язки в цілих числах при таких значеннях ![]() :
:
-
При
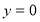 рівняння має вигляд:
рівняння має вигляд: 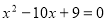
Тоді ![]() ;
; ![]() , тобто умові задачі задовольняють числа 10 і 90.
, тобто умові задачі задовольняють числа 10 і 90.
-
При
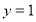 рівняння має вигляд:
рівняння має вигляд: 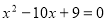
Тоді ![]() ;
; ![]() , тобто умові задачі задовольняють числа 11 і 91.
, тобто умові задачі задовольняють числа 11 і 91.
-
При
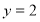 рівняння має вигляд:
рівняння має вигляд: 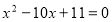
Тоді ![]() , тобто в цьому випадку рівняння не має розв’язків в цілих числах.
, тобто в цьому випадку рівняння не має розв’язків в цілих числах.
-
При
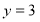 рівняння має вигляд:
рівняння має вигляд: 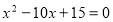
Тоді ![]() і в цьому випадку рівняння не має розв’язків в цілих числах.
і в цьому випадку рівняння не має розв’язків в цілих числах.
-
При
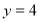 рівняння має вигляд:
рівняння має вигляд: 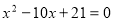
Тоді ![]() ;
; ![]() , тобто умові задачі задовольняють числа 34 і 74.
, тобто умові задачі задовольняють числа 34 і 74.
Відповідь: шукані двозначні числа: 10, 11, 34, 74, 90, 91.
Дослідження цього рівняння можна організувати іншим способом:
Перепишемо це рівняння у вигляді:
![]()
Послідовно підставляємо замість ![]() значення:
значення: ![]() .
.
При ![]() :
: ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
При ![]() :
: ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
При ![]() :
: ![]() ;
; ![]() -
- ![]() не має цілих значень.
не має цілих значень.
При ![]() :
: ![]() ;
; ![]() -
- ![]() не має цілих значень.
не має цілих значень.
При ![]() :
: ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
При ![]() значення виразу
значення виразу ![]() , тобто рівняння
, тобто рівняння ![]() не має дійсних розв’язків.
не має дійсних розв’язків.
Учням треба показати обидва способи, і обов’язково зробити висновок про раціональність.
Домашнє завдання:
Задача 3: Два двоцифрові числа 46 і 96 мають цікаву особливість: їх добуток не змінює величину, якщо цифри чисел переставити.
Дійсно, ![]() . Треба з’ясувати чи існують ще інші пари двозначних чисел з аналогічною властивістю. Як відшукати їх всі?
. Треба з’ясувати чи існують ще інші пари двозначних чисел з аналогічною властивістю. Як відшукати їх всі?
Розв’язання:
Позначимо цифри шуканих чисел через ![]() і
і ![]() ,
, ![]() і
і ![]() . Складемо рівняння:
. Складемо рівняння:
![]()
Розкриваємо дужки та спрощуємо:
![]() , де
, де
![]() ,
, ![]() ,
, ![]() ,
, ![]() - цілі числа
- цілі числа ![]() .
.
Для пошуку розв’язків складаємо із 9 цифр усі пари із рівними добутками.
Прибравши всі добутки, вибираємо тільки потрібні:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Усього рівностей 9. Із кожної можна скласти одну або дві шукані групи чисел. Наприклад, із рівності ![]() складаємо одне рішення:
складаємо одне рішення:
![]()
Із рівності ![]() знаходимо два рішення:
знаходимо два рішення:
![]() ,
, ![]()
Таким чином відшукуємо наступні 14 розв’язків :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: Пари двоцифрових чисел, добуток яких не змінюється при перестановці цифр чисел, наступні 12 і 42, 12 і 36, 12 і 84, 13 і 62, 13 і 93, 14 і 82, 23 і 64, 23 і 96, 24 і 63, 24 і 84, 26 і 93, 34 і 86, 36 і 84, 46 і 96.
Цій приклад треба почати на уроці: розібрати умову задачі, скласти рівняння, розглянути ідею розв’язування, а вже громіздкі обчислення та безпосередній перебір залишити додому.
3.1.2. Заняття № 2.
Тема уроку: Розв’язування діофантових рівнянь, використовуючи властивості подільності.
Мета уроку: формування вміння розв’язувати діофантові рівняння за допомогою властивостей подільності чисел; продовження формування вміння розв’язувати тестові задачі.
Хід уроку:
Почати урок слід з перевірки домашнього завдання.
Далі доцільно підвести дітей до висновку, що вивчений ними на минулому уроці метод не завжди раціональний, займає багато часу. Його зручно використовувати лише у випадках невеликого перебору.
Більш поширеним та дієвим найпростішим методом розв’язування діофантових рівнянь є метод, пов’язаний із властивостями подільності чисел.
Рівняння, що розв’язуються таким методом можна поділити на окремі групи. Кожній групі доцільно присвятити по цілому уроку. Метод доцільно детально розбирати на конкретних прикладах. Спочатку треба розглянути приклад з попереднього уроку.
Задача1. Знайти двозначне число, яке дорівнює подвоєному добутку його цифр.
Розв’язання: Склавши рівняння, маємо:
![]()
Звідси ![]()
Якщо уважно придивиться, то можна побачити, що вираз ![]() - ціле число.
- ціле число.
Отже, ![]() - парна цифра (ділиться на 2), більша 5 (
- парна цифра (ділиться на 2), більша 5 (![]() , бо інакше отримаємо
, бо інакше отримаємо ![]() ), тобто необхідно перевірити тільки значення
), тобто необхідно перевірити тільки значення ![]() ,
, ![]() . При
. При ![]() отримуємо
отримуємо ![]() . Не задовольняє умові задачі і
. Не задовольняє умові задачі і ![]() , бо у цьому випадку рівність
, бо у цьому випадку рівність ![]() дає
дає ![]() .
.
Відповідь : шукане число 36.
Треба звернути увагу учнів на те, що проста оцінка виразу (використали властивість подільності) звела перебор до мінімуму.
Отже, метод використання подільності чисел при розв’язуванні діофантових рівнянь полягає у наступному: треба рівняння представити у такому вигляді, щоб можна було легко оцінити вираз, використовуючи властивості подільності чисел, і вже потім конкретно перебирати декілька значень.
Задача2: Хлопці збирали гриби. Один з них знайшов 6 грибів, а інші по 13 грибів кожний. На наступний день кількість хлопців була іншою, один з них знайшов 5 грибів, а інші по 10 грибів кожний. Скільки хлопчиків збирали гриби у перший і другий день, якщо кількість зібраних грибів у обох була однакова? Відомо, що це ціле число більше за і менше за 200.
Розв’язання:
Для розв’язання цієї задачі достатньо введення двох невідомих.
Нехай у перший день збирали гриби ![]() хлопців, а у другий -
хлопців, а у другий - ![]() хлопців.
хлопців.
Тоді за умовою задачі отримуємо рівняння:
![]()
Виразимо одне невідоме через інше (у даному випадку зручніше виразити ![]() через
через ![]() , так як коефіцієнт біля
, так як коефіцієнт біля ![]() дорівнює 10, а подільність на 10 легко перевірити):
дорівнює 10, а подільність на 10 легко перевірити):
![]() .
.
Далі можна використати метод повного перебору, а саме послідовно перебрати натуральні значення ![]() і шукати ті з них, для яких значення
і шукати ті з них, для яких значення ![]() буде цілим. Однак цей шлях дуже громіздкий.
буде цілим. Однак цей шлях дуже громіздкий.
Легко бачити, що для подільності на 10 число ![]() повинно закінчуватися цифрою 0, але тоді число
повинно закінчуватися цифрою 0, але тоді число ![]() повинно закінчуватися цифрою 2. Так як останню цифра добутку одержуємо, коли множимо останні цифри множників,значить, число
повинно закінчуватися цифрою 2. Так як останню цифра добутку одержуємо, коли множимо останні цифри множників,значить, число ![]() повинно закінчуватись цифрою 4, тобто число
повинно закінчуватись цифрою 4, тобто число ![]() може бути рівним 4; 14; 24; ...
може бути рівним 4; 14; 24; ...
Але з умови задачі відомо, зо кількість грибів, зібраних у перший день, більша, ніж 100 і менша, ніж 200.
Підставляємо у вираз ![]() виділені значення
виділені значення ![]() , бачимо, що цій умові задовольняє лише
, бачимо, що цій умові задовольняє лише ![]() . Тоді
. Тоді ![]() .
.
Відповідь : у перший день збирали гриби 14 хлопців, а у другий 18 хлопців.
Задача 3. «Продаж курей» (старовинна задача). Три сестри прийшли на ринок із курьми. Одна принесла на продаж 10 курей, друга 16, третя 26. До полудня вони продали частину своїх курей за однією і тією ж ціною. Після полудня, побоюючись, що не всі кури будуть продані, вони знизили ціну та розпродали залишишок курей знов по однаковій ціні. Додому усі троє повернулися з однаковою виручкою: кожна сестра отримала від продажу 35 карбованців.
За якою ціною вони продавали курей до і після полудня?
Розв’язання:
Позначимо кількість курей, що продала кожна сестра до полудня через ![]() ,
, ![]() ,
, ![]() . У другій половині дня вони продали
. У другій половині дня вони продали ![]() ,
, ![]() ,
, ![]() курей. Ціну до полудня позначимо через
курей. Ціну до полудня позначимо через ![]() , після полудня через
, після полудня через ![]() .
.
|
Кількість проданих курей |
Ціна |
|||
|
До полудня |
|
|
|
|
|
Після полудня |
|
|
|
|
Перша сестра виручила:
![]() , отже,
, отже, ![]() .
.
Друга: ![]() , отже,
, отже, ![]() .
.
Третя: ![]() , отже,
, отже, ![]() .
.
Перетворимо ці три рівняння:
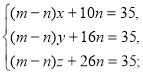
Віднімемо від третього рівняння перше, потім друге, отримаємо послідовно:
![]()
або
![]()
Розділимо перше із цих рівнянь на друге:
![]() , або
, або ![]() .
.
Так як ![]() ,
, ![]() ,
, ![]() - цілі числа, то і різниця
- цілі числа, то і різниця ![]() ,
, ![]() - теж цілі числа.
- теж цілі числа.
Отже, для існування рівності ![]() необхідно, щоб
необхідно, щоб ![]() ділилось на 8, а
ділилось на 8, а ![]() на 5. Отже
на 5. Отже ![]() .
.
Звідки: ![]()
![]() .
.
Відмітимо, що число ![]() - не тільки ціле, але й додатне, бо
- не тільки ціле, але й додатне, бо ![]() (у протилежному випадку перша сестра не могла б отримати грошей стільки ж, скільки третя).
(у протилежному випадку перша сестра не могла б отримати грошей стільки ж, скільки третя).
Так як ![]() , то
, то
![]() .
.
При цілих і додатних ![]() і
і ![]() остання нерівність задовольняється тільки в одному випадку: коли
остання нерівність задовольняється тільки в одному випадку: коли ![]() і
і ![]() .
.
Підставимо ці значення у рівняння:
![]() ,
, ![]() , знаходимо:
, знаходимо: ![]() ,
, ![]() .
.
Тепер повертаючись до рівняння:
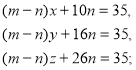
і підставляючи у них знайдені значення ![]() ,
, ![]() ,
, ![]() визнамо ціни зі якими продавали курей:
визнамо ціни зі якими продавали курей:
![]() крб.,
крб., ![]() крб..
крб..
Отже, курей продавали до полудня по 3 крб. 75 коп., після полудня по 1 крб. 25 коп.
Для самостійної роботи учнів:
Задача 4: який прямокутник? Сторони прямокутника виражаються цілими числами. Якої довжини повинні вони бути, щоб периметр прямокутника чисельно дорівнює його площі?
Розв’язання:
Позначимо сторони прямокутника через ![]() та
та ![]() , складаємо рівняння:
, складаємо рівняння:
![]()
Звідси випливає :
![]() .
.
Так як ![]() і
і ![]() мають бути додатними, то додатним повинно бути і число
мають бути додатними, то додатним повинно бути і число ![]() , тобто
, тобто ![]()
![]() 2.
2.
Перетворимо вираз так :
![]()
Так як ![]() повинно бути цілим числом, то вираз
повинно бути цілим числом, то вираз ![]() повинен бути цілим.
повинен бути цілим.
Але при ![]() це можливо лише, якщо
це можливо лише, якщо ![]() . Відповідними значеннями
. Відповідними значеннями ![]() будуть
будуть ![]() .
.
Відповідь : шукана фігура є або прямокутник зі сторонами 3 та 6, або квадрат із стороною 4.
Домашнє завдання:
Задача 5 : Знайти всі натуральні ![]() , при яких дріб
, при яких дріб ![]() буде цілим числом.
буде цілим числом.
Розв’язання :
Перепишемо наш дріб:
![]() .
.
За умовою це ціле число, отже ![]() - ціле число.
- ціле число.
Тоді ![]() цілий дільник числа 10. Цілими дільниками числа 10 є числа
цілий дільник числа 10. Цілими дільниками числа 10 є числа ![]() ;
;![]() ;
; ![]() ;
; ![]() . Прирівнюючи
. Прирівнюючи ![]() послідовно до кожного з цих чисел та вибираючи тільки натуральні розв’язки отриманих рівнянь, одержуємо, що при натуральних
послідовно до кожного з цих чисел та вибираючи тільки натуральні розв’язки отриманих рівнянь, одержуємо, що при натуральних ![]() дріб
дріб ![]() буде цілим числом.
буде цілим числом.
3.1.3 . Заняття № 3.
Тема уроку: Розв’язування діофантових рівнянь із використанням властивостей подільності чисел.
Мета уроку: формування вміння розв’язувати діофантові рівняння, використовуючи властивості подільності чисел.
Хід уроку:
На цьому уроці слід розглянути ще одну групу рівнянь, що розв’язуються методом використання властивостей подільності чисел.
Урок слід почати із розгляду приклада та детального його пояснення.
Задача 1. Знайти усі пари цілих чисел, що задовольняють рівнянню:
![]()
Розв’язання:
Представимо число 7 у вигляді добутку його дільників:
![]() ;
; ![]() .
.
Тепер перше рівняння можна переписати у вигляді двох систем:
а) ![]() б)
б) ![]()
Розв’язком системи а) є пара чисел: ![]() ,
, ![]() . Розв’язком системи б) є пара чисел:
. Розв’язком системи б) є пара чисел: ![]() ,
, ![]() .
.
Друге рівняння можна переписати теж у вигляді двох систем:
в) ![]() г)
г) ![]()
Розв’язком системи в) є пара чисел: ![]() ,
, ![]() . Розв’язком системи г) є пара чисел:
. Розв’язком системи г) є пара чисел: ![]() ,
, ![]() .
.
Отже, розв’язками вихідного рівняння є пари чисел: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Однак вже у другому прикладі одразу такий метод застосувати неможливо. Спочатку треба перетворити вираз, а вже потім застосовувати запропонований метод.
Задача 2. ![]() . Знайти цілі розв’язки.
. Знайти цілі розв’язки.
Розв’язання:
![]()
Перенесемо ![]() у ліву частину рівняння:
у ліву частину рівняння:
![]()
Легко бачити, що у лівій частині маємо різницю квадратів:
![]()
Отже, наше рівняння має вигляд:
![]() .
.
Замінимо дане рівняння рядом систем:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
д) ![]() е)
е) ![]() ж)
ж) ![]() з)
з) ![]()
Розв’язавши ці системи, можна переконатися, що рівняння не має розв’язків у цілих числах.
Ці системи розв’язувати зовсім не обов’язково. Слід тільки уважно придивитись і побачити, що сума та різниця тих самих цілих чисел у відповіді дають числа однієї парності (або сума та різниця це парні числа, або сума та різниця це непарні числа), а в нашому випадку жодна із систем не відповідає цій властивості, тобто одразу видно, що жодна із систем немає розв’язків у цілих числах.
Засвоєння учнями розглянутих прикладів, дозволяє розглянути більш складні приклади цього типу.
Задача 3. Розв’язати рівняння ![]() в цілих числах.
в цілих числах.
Розв’язання:
Зробимо доцільні перетворення рівняння, що вже більш складні, ніж у попередньому прикладі:
![]()
![]()
![]()
![]()
Тепер залишилося тільки перебрати усі можливі розкладення числа 4 у добуток цілих множників.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
д) ![]() є)
є) ![]()
Розв’язками цих систем, та нашого вихідного рівняння є пари чисел:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Приклади для самостійної роботи учнів:
Задача 4. Знайти усі пари натуральних чисел, що задовольняють рівнянню:
![]()
Розв’язання:
Перетворимо ліву частину нашого рівняння:
![]() .
.
Розкладемо число 105 на множники:
![]() .
.
Така рівність (при натуральних значеннях ![]() і
і ![]() ) можлива тільки у наступних випадках:
) можлива тільки у наступних випадках:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
(при натуральних значеннях ![]() і
і ![]()
![]() , тому система
, тому система
![]()
не може мати розв’язків у натуральних числах).
Розв’язуючи ці системи, отримуємо наступні розв’язки вихідного рівняння:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Задача 5. Знайти цілі розв’язки рівняння:
![]()
Розв’язок:
Перетворимо дане рівняння:
![]()
![]()
![]()
Дане рівняння можна замінити на такі системи:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
Розв’язками цих систем і нашого вихідного рівняння є пари чисел:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
Домашнє завдання:
Розв’язати рівняння в цілих числах:
а) ![]() .
.
б) ![]() у цілих натуральних числах.
у цілих натуральних числах.
Відповіді:
1) Рівняння перетворюється:![]()
Відповідь: ![]() ;
; ![]()
2) Відповідь: ![]() .
.
3.1.4.Заняття № 4.
Тема уроку: Задачі, що зводяться до розв’язування рівнянь із одним невідомим у цілих числах, використовуючи властивості подільності чисел.
Мета уроку:
- продовження формування вміння розв’язувати текстові задачі
- сформувати вміння розв’язувати задачі, що зводяться до розв’язування рівнянь у цілих числах.
Хід уроку:
На початковому етапі уроку слід перевірити домашнє завдання.
Сформувати алгоритми розв’язування діофантових рівнянь, використовуючи властивості подільності чисел.
Задача 1: Фірма заказала 143 комп’ютери, для того щоб розподілити їх між своїми філіями порівну. Однак потім фірма вирішила відкрити ще дві філії, і в результаті кожна філія отримала на 2 комп’ютери менше.
Скільки у фірми стало філій?
Розв’язання:
Позначимо початкову кількість філій через ![]() . Тоді за умовою задачі кожна філія повинна була отримати
. Тоді за умовою задачі кожна філія повинна була отримати ![]() комп’ютера. Але філій стало
комп’ютера. Але філій стало ![]() , і, отже кожна філія отримала
, і, отже кожна філія отримала ![]() комп’ютери.
комп’ютери.
За умовою задачі кожна філія отримала на 2 комп’ютери менше.
Складемо рівняння:
![]() .
.
Згадаємо, що ![]() - кількість філій фірми і, отже – це натуральне число. Крім того
- кількість філій фірми і, отже – це натуральне число. Крім того ![]() та
та ![]() - теж натуральні числа, оскільки кожне із них – це кількість комп’ютерів.
- теж натуральні числа, оскільки кожне із них – це кількість комп’ютерів.
Отже, числа ![]() та
та ![]() - дільники числа 143. Залишається знайти усі дільники числа 143 та вибрати такі два дільники, один із яких на 2 більше другого.
- дільники числа 143. Залишається знайти усі дільники числа 143 та вибрати такі два дільники, один із яких на 2 більше другого.
У числа 143 лише чотири дільники:
![]() .
.
Перебравши усі можливі пари дільників, легко побачити, що умові задовольняє лише пара чисел 11; 13.
Отже ![]() , а
, а ![]() .
.
Відповідь: у фірмі стало 13 філій.
Задача 2: Андрійко задумав деяке натуральне число. Борис запропонував йому піднести це число до другого степеня, після цього додати задумане число і назвати результат. Результат дорівнював 90. Як Борису дізнатись, яке число задумав Андрій?
Розв’язання:
Позначимо задумане число через ![]() . Тоді можна скласти рівняння:
. Тоді можна скласти рівняння:
![]() або
або ![]() .
.
Тепер ясно, що треба знайти натуральне число ![]() таке, що при множенні його на наступне натуральне число у добутку будемо мати 90. Такі два натуральні числа неважко підібрати – це 9 та 10.
таке, що при множенні його на наступне натуральне число у добутку будемо мати 90. Такі два натуральні числа неважко підібрати – це 9 та 10.
Отже, ![]() .
.
Здається, що задача розв’язана, але це не так. Раптом є ще будь-яке натуральне число, що задовольняє умові ![]() ? Бо в даному випадку ми не перебирали усі можливі варіанти розв’язків, а лише підібрали відповідь.
? Бо в даному випадку ми не перебирали усі можливі варіанти розв’язків, а лише підібрали відповідь.
Для того, щоб впевнитись у відсутності іншого такого числа, треба провести додаткові міркування: якщо ![]() то
то ![]() , тоді добуток
, тоді добуток ![]() більше
більше ![]() , тобто більше 90.
, тобто більше 90.
Аналогічно: ![]() не може бути менше 9, бо в цьому випадку добуток
не може бути менше 9, бо в цьому випадку добуток ![]() . Отже могло бути задумане лише число 9.
. Отже могло бути задумане лише число 9.
Відповідь: задумане число 9.
Дуже часто в олімпіадних задачах зустрічаються такі, що зводяться до розв’язування системи нелінійних рівнянь, що мають кількість невідомих більшу ніж кількість рівнянь, у цілих числах. Тому у курс обов’язково треба включити такі завдання для загального ознайомлення. Деякі системи зводяться до розв’язування діофантового рівняння, використовуючи властивості подільності чисел. Пропонуємо включити декілька систем у цей урок.
Приклад 1: Розв’язати в натуральних числах:
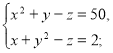
Розв’язання:
Віднімемо почленно із першого рівняння системи друге:
В результаті отримаємо:
![]()
Тепер треба перетворити ліву частину таким чином, щоб отримати добуток многочленів:
![]()
![]()
![]()
Тепер за звичною системою: розглянемо усі розкладення числа 48 на дільники.
Маємо ряд систем:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]() 7)
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
Розв’язавши ці системи, знаходимо два розв’язки у натуральних числах рівняння:
![]() .
.
![]() ;
; ![]() .
.
Тепер треба повернутися до вихідної системи, з метою її розв’язків. Для цього у будь-яке рівняння системи підставляємо отримані пари чисел і знаходимо розв’язки самої системи, а саме:
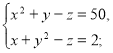
Підставимо наші пари чисел у перше рівняння системи:
Якщо ![]() ,
, ![]() , то
, то ![]() . Тобто, розв’язком системи в цьому випадку є трійка чисел:
. Тобто, розв’язком системи в цьому випадку є трійка чисел: ![]() .
.
Якщо ![]() ,
, ![]() , то
, то ![]() . Тобто, розв’язком системи в цьому випадку є трійка чисел:
. Тобто, розв’язком системи в цьому випадку є трійка чисел: ![]() .
.
Для самостійної роботи учнів:
Приклад 2: Знайти усі натуральні ![]() ,
, ![]() ,
, ![]() , що задовольняють системі:
, що задовольняють системі:
![]()
Розв’язок:
Віднімемо перше рівняння від другого:
![]()
Перетворимо ліву частину у добуток многочленів:
![]()
![]()
З цього рівняння отримуємо дві системи:
1) ![]() 2)
2) ![]()
Для першої системи:
![]()
Підставляємо ці значення ц вихідну систему і отримаємо, в цьому випадку, розв’язок у вигляді: ![]() .
.
Приклад: Знайти натуральний розв’язок рівняння: ![]() .
.
Розв’язок:
Дільники числа 6: ![]() .
.
Нас задовольняють два числа, які відрізняються на одиницю і у добутку дають число 6. Легко бачити, що це числа 3 і 2.
Отже, ![]() .
.
Приклад 3: знайти натуральні розв’язки рівняння:
![]()
Відповідь: ![]() .
.
Домашнє завдання:
1) Знайти натуральний корінь рівняння:
![]()
Відповідь: ![]()
2) Знайти усі цілі корені рівняння:
![]()
Відповідь: ![]() ;
; ![]() .
.
3) Знайти натуральні корені рівняння:
![]()
Відповідь: ![]() .
.
3.1.5.Заняття № 5.
Тема уроку: Розв’язування діофантових рівнянь методом виділення цілої частини.
Мета уроку:
- сформувати вміння розв’язувати діофантові рівняння методом виділення цілої частини.
- продовження формування вміння розв’язувати текстові задачі.
Хід уроку:
Метод виділення цілої частини – є загальним методом для розв’язання у цілих числах невизначених (діофантових) рівнянь. Він був названий у Індії методом розсіювання (роздроблення). Натяки саме на таке розв’язування зустрічаються вперше у працях індійського астронома Аріабхатти, подібне розв’язування виклали індійські математики Брахмагупта та Бхагкара, бо саме у Індії невизначені рівняння розв’язувалися із астрономічними запросами та календарними розрахунками, тому ними займались астрономи та математики.
Використаємо цей метод для розв’язування наступних задач.
Задача 1: Знайти два цілих числа, якщо відомо, що різниця добутків першого на 19 і другого на 8 дорівнює 13.
Розв’язок:
У задачі треба знайти усі цілі розв’язки рівняння: ![]() (1).
(1).
Виразимо ![]() - невідоме з найменшим за абсолютною величиною коефіцієнтом- через
- невідоме з найменшим за абсолютною величиною коефіцієнтом- через ![]() , отримаємо:
, отримаємо: ![]() (2).
(2).
Тепер треба дізнатись, при яких цілих значеннях ![]() відповідні значення
відповідні значення ![]() є також цілими числами. Перепишемо рівняння (2) у наступному вигляді:
є також цілими числами. Перепишемо рівняння (2) у наступному вигляді: ![]() (3).
(3).
З таким прийомом ми вже зустрічалися при розгляді попереднього метода. Із (3) випливає, що ![]() при цілому
при цілому ![]() приймає цілі значення тільки в тому випадку, якщо вираз
приймає цілі значення тільки в тому випадку, якщо вираз ![]() є цілим числом, наприклад
є цілим числом, наприклад ![]() .
.
Поклавши ![]() (4), питання зводимо до розв’язку у цілих числах рівняння (4) з двома невідомими
(4), питання зводимо до розв’язку у цілих числах рівняння (4) з двома невідомими ![]() і
і ![]() ; його можна записати так:
; його можна записати так:
![]() (5).
(5).
Це рівняння у порівнянні із вихідним має перевагу: 3 – найменша із абсолютних величин коефіцієнтів при невідомих – менша, ніж у (1), тобто 8. Це було досягнуто завдяки тому, що коефіцієнт при ![]() (19) було замінено залишком від ділення на 8.
(19) було замінено залишком від ділення на 8.
Продовжуючи аналогічним способом, ми із (5) отримаємо:
![]() (6)
(6)
Отже, невідоме ![]() при цілому
при цілому ![]() тільки тоді приймає цілі значення, коли
тільки тоді приймає цілі значення, коли ![]() є ціле число, скажемо
є ціле число, скажемо ![]() :
:
![]() (7)
(7)
або ![]() (8)
(8)
Далі,
![]() (9)
(9)
Покладемо
![]() (10)
(10)
отримаємо рівняння:
![]() (11)
(11)
Це саме просте із всіх розглянутих невизначених рівнянь, бо один із коефіцієнтів дорівнює одиниці.
Із (11) отримаємо:
![]() (12)
(12)
Звідси видно, що ![]() приймає цілі значення при будь яких цілих значеннях
приймає цілі значення при будь яких цілих значеннях ![]() . Із рівностей (6), (9), (12), (3) шляхом послідовних підстановок можна знайти наступні вирази для невідомих
. Із рівностей (6), (9), (12), (3) шляхом послідовних підстановок можна знайти наступні вирази для невідомих ![]() і
і ![]() рівняння (1):
рівняння (1):
![]()
![]()
Таким чином формули:
![]()
![]() , при
, при ![]() дають цілі розв’язки рівняння (1).
дають цілі розв’язки рівняння (1).
Наведемо приклади розв’язків у таблиці.
|
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
7 |
15 |
23 |
31 |
39 |
47 |
55 |
63 |
71 |
|
|
15 |
34 |
53 |
72 |
91 |
110 |
129 |
148 |
167 |
Цей прийом майже повністю співпадає із методом індійців і був названий ними методом розсіювання саме тому, що невизначене рівняння зводиться до ланцюга рівнянь із все меншими, за абсолютною величиною, коефіцієнтами.
Цей приклад треба розглядати дуже детально, записувати пояснення до кожного кроку, бо розв’язання є алгоритмом розв’язку діофантових рівнянь таким методом.
До розв’язування таких невизначених рівнянь зводяться іноді задачі, пов’язані із практикою і повсякденною діяльністю людини.
Задача 2: Чоловік купує у магазині річ вартістю у 19 крб. У нього є лише 15 купюр по три крб., у касира лише 20 купюр по п’ять крб. Чи можна розрахуватися і як?
Розв’язання:
Задача зводиться до розв’язку у цілих додатних числах числах діофантового рівняння:
![]() , де
, де ![]() ,
, ![]()
Більш того ![]() , бо
, бо ![]()
![]()
Далі,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Звідки ![]() ,
, ![]() .
.
В силу того, що ![]() і
і ![]() повинні бути додатними, та враховуючи умову задачі, легко встановити, що
повинні бути додатними, та враховуючи умову задачі, легко встановити, що
![]() ,
,
тобто ![]() може приймати тільки два значення: 0; 1. Звідси випливають два можливі розв’язки.
може приймати тільки два значення: 0; 1. Звідси випливають два можливі розв’язки.
|
|
8 |
13 |
|
|
1 |
4 |
Для самостійного розв’язку учнів:
Задача 3: Чи можна зважити 28 г деякої речовини на терезах, маючи тільки чотири ваги масою 3 г і сім - масою 5г?
Розв’язання:
Розв’яжемо діофантове рівняння:
![]()
Маємо:
![]() ,
,
![]() ,
, ![]() ,
,
![]()
Отже,
![]()
![]()
Із умови задачі випливає, що ![]() не може набувати від’ємні значення (бо це призведе до від’ємного
не може набувати від’ємні значення (бо це призведе до від’ємного ![]() ).
).
Також ![]() , отже,
, отже, ![]() .
.
Однак ![]() і
і ![]() суперечить умові задачі, тобто за умовою
суперечить умові задачі, тобто за умовою ![]() . Таким чином, можливо лише
. Таким чином, можливо лише ![]() . При цьому
. При цьому ![]() ,
, ![]() єдиний розв’язок задачі.
єдиний розв’язок задачі.
Багато старовинних способів відгадування чисел і дат народження засновано на розв’язанні діофантових рівнянь.
Задача 4:
Ви пропонуєте товаришу помножити число дати його народження на 12, а номер місяця – на 31. Він повідомляє вам суму обох добутків, а ви розраховуєте по ній дату народження друга.
Якщо, наприклад, товариш ваш народився 9 лютого, то він робить наступне:
![]() ,
, ![]() ,
,
![]()
Це останнє число, 170, він вам повідомляє, а ви з’ясовуєте задуману дату. Як?
Розв’язання:
Задача зводиться до розв’язку невизначеного рівняння:
![]()
У цілих і додатних числах, причому число місяця ![]() не більше 31, а номер місяця
не більше 31, а номер місяця ![]() не більше 12.
не більше 12.
![]() ,
,
![]()
![]()
![]() ,
, ![]()
![]()
![]()
Знаючи, що ![]() і
і ![]() знаходимо границі для
знаходимо границі для ![]() :
: ![]() .
.
Отже: ![]() ,
, ![]() ,
, ![]() .
.
Дата народження 9-е число другого місяця, тобто 9 лютого.
Для самостійного розв’язку учнів:
Задача 5: Знайти дату народження, якщо сума добутків дорівнює 330.
Розв’язання:
Розв’яжемо невизначене рівняння:
![]()
За допомогою метода розсіювання отримаємо:
![]()
![]()
Із умови
![]()
![]()
Легко констатувати, що єдине рішення
![]() ,
, ![]() ,
, ![]() .
.
Отже, дата народження: 12-е число, 6-го місяця, тобто 12 червня.
Домашнє завдання:
Задача 6: Треба на один карбованець купити 40 штук поштових марок: по одній копійці – по 4-и копійки і по 12 копійок. Скільки марок кожної ціни можна купити?
Розв’язання:
У даному випадку маємо два рівняння із трьома невідомими:
![]()
![]()
де: ![]() - кількість марок по копійці;
- кількість марок по копійці;
![]() - по 4 копійки;
- по 4 копійки;
![]() - по 12 копійок.
- по 12 копійок.
Віднімемо із першого рівняння друге, одержимомо одне рівняння з двома невідомими:
![]()
Знаходимо ![]() :
:
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Підставимо вирази для ![]() і
і ![]() у друге із вихідних рівнянь:
у друге із вихідних рівнянь:
![]()
Одержуємо:
![]()
Так як ![]() ,
, ![]() ,
, ![]() .
.
![]()
Тобто ![]() ,
, ![]()
|
|
0 |
1 |
|
|
20 |
28 |
|
|
20 |
9 |
|
|
0 |
3 |
Перевірка:
![]()
![]()
Отже, марки можна купити двома способами.
Перед тим як задати цю задачу додому треба зробити коментар до неї, а саме пояснити як скласти систему рівнянь.
Другу аналогічну задачу задати без коментарю.
Задача 7:
На 5 крб. купити 100 різних фруктів. Ціни на фрукти такі:
|
кавун |
шт. |
50 коп. |
|
яблуко |
шт. |
10 коп. |
|
слива |
шт. |
1 коп. |
Скільки фруктів кожного роду було куплено?
Відповідь: 1 кавун, 39 яблук, 60 слив.
3.1.6. Заняття № 6.
Тема уроку: Загальна схема розв’язування лінійних діофантових рівнянь.
Мета уроку:
- ознайомити учнів із поняттям лінійного діофантового рівняння та загальною схемою його розв’язання.
- сформувати вміння розв’язувати лінійні діофантові рівняння, використовуючи загальну схему їх розв’язання.
Хід уроку:
Після того, коли учні усвідомили найпростіші методи розв’язування діофантових рівнянь, слід перейти до більш складного матеріалу, а саме до специфічних методів розв’язування лінійних діофантових рівнянь.
Для більш глибокого усвідомлення учнями загальної схеми розв’язування лінійних діофантових рівнянь, розглянемо її застосування на прикладі.
Приклад 1: Розв’язати рівняння ![]() у цілих числах.
у цілих числах.
Розв’язання:
Знайдемо спочатку будь-який конкретний розв’язок цього рівняння, звичайним підбором:
Так як ![]() , то
, то
![]() і отже,
і отже,
![]() ,
, ![]() - це конкретний розв’язок нашого рівняння (один з багатьох, не більше!) отже,
- це конкретний розв’язок нашого рівняння (один з багатьох, не більше!) отже,
![]() ;
; ![]() .
.
Тепер віднімемо одне рівняння від другого:
![]() ,
,
![]() ,
,
![]() .
.
У останньому рівнянні позначимо ![]() через
через ![]() , а
, а ![]() через
через ![]() , тобто:
, тобто:
![]()
Звідси легко бачити, що ![]() ділиться на 3, а
ділиться на 3, а ![]() на 5.
на 5.
Отже, покладемо ![]() , тоді
, тоді ![]() , тут
, тут ![]() , очевидно, може бути будь-яким цілим числом. Тепер, якщо повернутися назад, до заміни, ми одержимо набір розв’язків:
, очевидно, може бути будь-яким цілим числом. Тепер, якщо повернутися назад, до заміни, ми одержимо набір розв’язків:
![]()
![]() , тобто
, тобто
![]()
![]() , де
, де ![]() може бути будь-яким цілим числом.
може бути будь-яким цілим числом.
Останні вирази для ![]() та
та ![]() і є загальним розв’язком даного лінійного рівняння в цілих числах.
і є загальним розв’язком даного лінійного рівняння в цілих числах.
Після розгляду приклада, доцільно показати учням лінійне рівняння та його розв’язки у загальному вигляді.
Теорема: Якщо пара цілих чисел ![]() ,
, ![]() задовольняє рівнянню:
задовольняє рівнянню:
![]() , де
, де ![]() ,
, ![]() ,
, ![]() - цілі числа і НСД
- цілі числа і НСД ![]() , то
, то ![]() ,
, ![]() , де
, де ![]() - довільне ціле число, є спільним розв’язком цього рівняння в цілих числах.
- довільне ціле число, є спільним розв’язком цього рівняння в цілих числах.
Приклад 2: Розв’язати рівняння у цілих числах: ![]() .
.
Розв’язання:
НСД ![]() , також 15 не ділиться на НСД
, також 15 не ділиться на НСД ![]() , тобто це рівняння не має розв’язків у цілих числах.
, тобто це рівняння не має розв’язків у цілих числах.
Звичайно, інших розв’язків рівняння ![]() не має, цей момент учні повинні дуже чітко усвідомлювати.
не має, цей момент учні повинні дуже чітко усвідомлювати.
Не розуміючи того, що пари ![]() вичерпують усі розв’язки даного рівняння, неможливо рухатися далі.
вичерпують усі розв’язки даного рівняння, неможливо рухатися далі.
Доводити цю теорему недоцільно, бо розв’язання конкретного лінійного рівняння по суті і є доведенням цієї теореми, а доцільно запропонувати самостійно розв’язати приклад з повним виведенням формул для загального розв’язку.
Приклад 3: Розв’язати рівняння ![]() в цілих числах.
в цілих числах.
Розв’язання:
Розділимо обидві частини рівняння на НСД ![]() , отримаємо рівносильне рівняння:
, отримаємо рівносильне рівняння:
![]()
НСД ![]() .
.
Знайдемо конкретний розв’язок даного рівняння:
Так як ![]() , отже
, отже ![]() ,
, ![]() - конкретний розв’язок нашого рівняння.
- конкретний розв’язок нашого рівняння.
Отже, ![]() ;
; ![]() .
.
Почленно віднімемо одне рівняння від другого:
![]()
![]()
Позначимо ![]() за
за ![]() , а
, а ![]() за
за ![]() .
.
Отже, ![]()
Тепер видно, що ![]() ділиться на 1, а
ділиться на 1, а ![]() - кратне 4, а отже можна покласти, що:
- кратне 4, а отже можна покласти, що:
![]() ;
; ![]() .
.
Повертаємося до заміни:
![]()
![]() , тобто
, тобто
![]()
![]() , де
, де ![]() може бути будь яким цілим числом.
може бути будь яким цілим числом.
Наступні приклади краще розв’язувати використовуючи сформульовану теорему.
Приклад 4: Розв’язати рівняння ![]() в цілих числах.
в цілих числах.
Розв’язання:
За теоремою, треба знайти будь-який конкретний розв’язок рівняння.
Так як ![]() , то
, то ![]() ,
, ![]() - конкретний розв’язок даного рівняння.
- конкретний розв’язок даного рівняння.
Отже, за теоремою:
![]()
![]() .
.
З нашого рівняння: ![]() ,
, ![]() .
.
Тобто: ![]()
![]() , де
, де ![]() - довільне ціле число.
- довільне ціле число.
Для самостійного розв’язку учнів:
Приклади: Знайти цілі розв’язки рівнянь:
а)![]() с)
с) ![]()
б) ![]() д)
д) ![]()
Розв’язання:
а) ![]()
Знайдемо конкретний розв’язок рівняння:
![]() , тобто
, тобто
![]() ,
, ![]() - конкретний розв’язок рівняння. Для даного рівняння
- конкретний розв’язок рівняння. Для даного рівняння ![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
б) ![]()
Знайдемо конкретний розв’язок:
![]() . Отже
. Отже ![]() ,
, ![]() - конкретний розв’язок рівняння.
- конкретний розв’язок рівняння.
Для цього рівняння ![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
с) ![]()
Конкретний розв’язок:
![]()
![]() ,
, ![]() .
.
Для даного рівняння ![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
д) ![]()
Конкретний розв’язок:
![]()
![]() ,
, ![]() .
.
Для даного рівняння ![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
Домашнє завдання:
1. Розв’язати рівняння ![]() у цілих числах (вивести формули для загального розв’язку).
у цілих числах (вивести формули для загального розв’язку).
Відповідь: ![]()
![]() ,
, ![]() .
.
2. Розв’язати рівняння у цілих числах:
а) ![]() б)
б) ![]()
Відповідь:
а) ![]() б)
б) ![]()
![]() ,
, ![]()
![]() ,
, ![]() .
.
Висновки.
Проблема розв’язування діофантових рівнянь являє собою одну з найбільш складних та цікавих проблем теорії чисел. Тому дуже багато математиків у своїх роботах приділяють особливу увагу питанням розв’язку діофантових рівнянь. Це стосується як вчених давнини: Піфагора, Діофанта Олександрійського, Брахмагупти, Пхаскари, так і вчених більш близької доби: П. Ферма, Ж.Л. Лагранжа.
Однак, ця проблема розв’язана не до кінця. Лише для рівнянь другого степеню з двома невідомими вона розв’язана повністю. Це означає, що немає такого алгоритму, користуючись яким можна було б про всяке діофантове рівняння сказати, чи розв’язане воно в цілих числах. Якби такий алгоритм існував, то достатньо було б його застосувати до рівняння Ферма, щоб питання про розв’язаність чи нерозв’язаність цього рівняння в цілих числах було з’ясоване. Але загального порядку дій немає, і теорема Ферма продовжує хвилювати уми математиків.
І все ж не слід відмовлятись від спроб знайти доведення теореми. Адже заняття математикою – це своєрідна безпрограшна лотерея. Не розв’язавши проблеми, ви, однак завжди знайдете багато важливих і корисних результатів.
Завдання, які зводяться до діофантових рівнянь, дуже часто зустрічаються на математичних олімпіадах різних рівнів. Тому доцільно познайомити учнів з основними поняттями, пов’язаними із діофантовими рівняннями та ідеями розв’язування задач, які до них зводяться.
В даній роботі виділено основні методи розв’язування задач, пов’язаних із діофантовими рівняннями; підібрано різнорівневу систему завдань для відпрацювання кожного методу; розроблено систему занять по ознайомленню учнів із завданнями, що зводяться до таких рівнянь.
За рахунок того, що в роботі підібрано різнорівневу систему вправ, розроблені матеріали можна використовувати при роботі з учнями як 6-7 так і 8-9 класів.Розроблені матеріали частково апробувалися під час підготовки до II етапу олімпіади з математики учнів 8-9 класів Ізюмської ЗОШ I-III ступенів №11.
Література
- Кованцов М.І. Математична хрестоматія. Алгебра і початки аналізу. – 1977. – с.25, 91-92.
- Миронюк В., Ясінський М. Методика розв’язування олімпіадних задач, пов’язаних з показниковими та степенево-показниковими діофантовими рівняннями. // Математика в школі. – 2005. – №3 . – с.47-49.
- Плис Т.В. Вивчення діофантових рівнянь у шкільному курсі алгебри. // Математика в школах України. – 2006. – №35. – с.21-24.
- Малинин В. Решение уравнений в натуральных числах. //Математика. – 2001. – №2. – с.25-28.
- Черепинський О. Розв’язування рівнянь у цілих числах. // Математика. – 2005. – №29-30. – с.22-26.
- Тищенко В.В. Діофантові рівняння. http://klasnaocinka.com.ua/ru/article/diafantovi-rivnyannya-tvorcha-robota.html
- Чемерис М І. http://metodportal.net/node/5645


про публікацію авторської розробки
Додати розробку
