Нестандартний урок як шлях формування компетентності учнів.
Автор- упорядник:
Мирошничекно Наталія Костянтинівна, вчитель математики, спеціаліст І категорії.
Нестандартний урок як шлях формування компетентності учнів.
Об’єктом дослідження даної роботи виступає нестандартне викладання математики в основній школі. Методика викладання математики має певні специфічні риси стосовно формування компетентностей учнів. Саме уроки математики дають виключні можливості прищеплювати інтерес до творчих пошуків, виховувати в дітей бажання шукати нові, кращі шляхи виконання дорученої справи.
Робота призначена для вчителів математики.
Зміст
Вступ………………………………………………………………...2
Розділ I . Компетентністно орієнтований підхід до навчання……..…...4
1.1.Компетентність як педагогічне явище ………………………………..4
1.2Можливості математики щодо формування основних груп компетентностей учнів…………………………………………………………….6
II. Нестандартний урок як шлях формування компетентності учнів………………………………………………………………………………...10
2.1 Урок як основна форма організації навчання………………...……..10
2.2 Підготовка до уроку…………………………………………………….13
2.3Нестандартний урок як форма організації навчання……………….14
2.4Розробка й проведення уроку-казки та уроку-гри…………………..18
Додаток А) Урок-гра………………………………………………………20
Додаток Б) Урок-подорож ………………………………………………..31
Додаток В) Урок-гра ………………………………………………………34
Література…………………………………………………………………..35
Вступ
Школа — це перше випробування в житті, і тільки вчитель може допомогти гідно пройти через нього. І вчителі намагаються. Вони роблять усе можливе. І навіть більше.
Роль учителя є вирішальною у процесах формування мислення, гартування характеру й виховання моральних якостей учня. Він генератор і джерело ідей, якими керується другий суб'єкт педагогічного процесу - учень. Від педагогічної майстерності вчителя залежить націлювання учнів на належний навчальний лад. Тоді цілі вчителя стають і цілями учнів — у них одна мета. Природно, що прагнення обох до єдиної мети прискорює її досягнення. Щоб керувати процесом формування і розвитку здібностей учнів, треба знати актуальні і потенціальні їх рівні. Водночас виникає проблема: якими повинні бути умови середовища, щоб кожен школяр міг розвинути свої творчі нахили й перетворити їх у творчі досягнення. Високий рівень успішності учнів не завжди поєднується з високим рівнем творчої обдарованості. У зв'язку з цим потрібно намагатися створити сприятливі умови для самовираження кожної дитини в різних видах діяльності, в тому числі й навчально-творчій.
Саме уроки математики дають виключні можливості прищеплювати інтерес до творчих пошуків, виховувати в дітей бажання шукати нові, кращі шляхи виконання дорученої справи.
Працюючи вшколі та спостерігаючи за школярами, я дійшла висновку, що для багатьох учнів визначальним чинником вивчення математики є її загальновизнана роль у житті та інших науках. Але є учні, які на уроці перестають слухати або, навпаки, тільки роблять вигляд, що слухають, але не чують, якщо новий матеріал їх не зацікавив з самого початку. Запобігаючи байдужості на уроці, появу нового матеріалу потрібно підпорядковувати природній допитливості школяра: новий факт не виникає з «нічого»; разом з дітьми з'ясувати можливості його застосування, а форму організації навчання обирати оптимальною. Отже, завдання, яке постало перед учителем, — збудити здібності своїх учнів, виховати в них сміливість думки і впевненість у тому, що вони розв'яжуть кожну задачу, в тому числі й творчого характеру, — без особистого захоплення справою, без наявності педагогічного такту і таланту, без умілого вибору форм навчання, методів, прийомів та засобів втілити в життя неможливо.
Для учня - посильним і успішно- результативним, для вчителя - радісним. Творчо працюючи, він завжди прагне:
-
пропонувати посильний рівень вимог відповідно до рівня навченості та научуваності;
вчити учнів концентруватися та максимально викладатися в обмежений час; - дати можливість навіть слабкому учневі отримати високу оцінку;
- створювати умови для свідомого і самостійного вибору учнями рівня засвоєння навчального матеріалу;
-
дати можливість сильним учням проявити свої творчі здібності.
Адже інтерес до діяльності має спеціальну здатність підвищувати працездатність включаючи увагу. Підтримання бажання вчитися вимагає зміни способів і форм сприйняття нового, створення різних ситуацій для застосування вивченого. Виховання ж інтересу передбачає реалізацію багатьох методичних прийомів, пошук і застосування різних технологій навчання, а головне — невтомну вчительську працю, самовдосконалення і самоосвіту.
Високий рівень успішності учнів не завжди поєднується з високим рівнем творчої обдарованості. У зв'язку з цим потрібно намагатися створити сприятливі умови для самовираження кожної дитини в різних видах діяльності, в тому числі й навчально-творчій.
Розділ I .Компетентністно орієнтований підхід до навчання
1.1.Компетентність як педагогічне явище.
Існують декілька способів формування життєвої компетентності учнів. Одним із них є цілеспрямований розвиток у сім'ї,
Умовно визначають 9 груп компетенцій, які називають ключовими. Ключові компетенції, характеризуються як такі, що:
- мають змогу вирішувати складні (не алгоритмізовані) завдання;
- є поліфункціональними (дають змогу розв'язувати різні проблемні завдання з певної діяльності);
- можуть транслюватися на різні види діяльності;
- реалізуються на різних рівнях, складно побудовані (передбачають когнітивні, операційні, аксіологічні та поведінкові утворення)..
На основі одержаних даних та спираючись на наукові погляди вчених щодо класифікацій життєвої компетентності (І. Єрмаков, В. Зарицька, Д. Пузіков, І. Родигі- на та ін.), визначили 9 складових життєвої компетенції учнів НВК (див. табл.)
1. Життєтворчі компетенції, які полягають у здатності- самостійно, свідомо і творчо визначати, проектувати і здійснювати особисте життя.
2. Життєздатні компетенції—це сукупність здібностей особистості, які пов'язані з її спроможністю розвивати та відтворювати на якісно вищому рівні свій життєвий потенціал, застосовувати його для успішного, свідомого і творчого вирішення життєвих завдань, творення свого життя.
3. Компетенції навчатися впродовж життя — це здатність і готовність ефективно використовувати і швидко поповнювати, розширювати, інтегрувати особистий досвід (зокрема знання, вміння, навички) для вирішення нестандартних життєвих завдань.
4.Соціальні компетенції — це здатність і готовність особистості до соціальної дії, соціальної активності та мобільності, набуття й виконання пов'язаних із ними соціальних ролей.
5.Комунікативні компетенції передбачають сукупність здібностей, пов'язаних з ефективним спілкуванням: володіння рідною та іноземними мовами, знання, уміння й навички, пов'язані із застосуванням засобів комунікації; наявність умінь, пов'язаних із розумінням психологічних особливостей спілкування, здатність і готовність до реалізації навичок уникнення та розв'язання конфліктів, володіння навичками самопрезентації.
6.Інформаційні компетенції — це сукупність здібностей, які визначають успішність участі особистості в різноманітних інформаційних процесах, що відбуваються в суспільстві, визначають спроможність особистості шукати, опрацьовувати, використовувати, зберігати та передавати різноманітну інформацію.
7.Політичні (політико- правові) компетенції — це сукупність здібностей, які визначають рівень політичної та правової культури особистості, міру та успішність її політичної активності, відповідність її життєдіяльності правовим нормам, встановленим державою.
8.Трудові (професійні) компетенції — це здатність і готовність особистості до продуктивної. трудової діяльності, пов'язаної з побутом, господарюванням, професійними обов'язками; набуття нових професійних навичок, здатність і готовність підвищувати свою професійну кваліфікацію, оволодівати суміжними і новими напрямами діяльності.
9.Компетенції здорового способу життя.
Критерії компетенції:
- Раціональна організація діяльності та дозвілля.
- Дотримання морально-гігієнічних та санітарно-гігієнічних норм.
- Виконання заходів особистої гігієни та психогігієни.
- Підтримання активного рухового режиму та систематичних занять фізкультурою.
- Підтримання раціонального режиму харчування.
- Опір шкідливим звичкам, негативним соціальним явищам.
1.2Можливості математики щодо формування основних груп компетентностей учнів.
Методика викладання математики має певні специфічні риси стосовно формування компетентностей учнів.
Соціальна компетентність
1.Вибір учнів завдань ,які передбачають для учнів самостійний пошук їх розв’язання .
2.Надання учням можливості обрання варіанту завдання чи шляху розв’язання задач.
3.Надання учням можливості вибору творчих чи експериментальних завдань.
4.Використання самооцінки та взаємооцінки учнів.
5.Розв’язання задач різними способами та визначення раціонального шляху розв’язання.
6.Залучення дітей до роботи в групах.Обов’язкова умова – врахування індивідуальних можливостей школярів.Завданя мають бути якщо не індивідуальними то хоча б рівневими.
7.Надання учням можливості виявленя ініціативи.
8.Практикування доручень учням ,наприклад, «відповідальний за наочність », «консультант» тощо.
9. Проведення виховних годин у формі дискусій.
10.Планування виховних заходів та заходів предметних тижнів,у яких передбачається самостійна діяльність учнів.
11.Залучення дітей до самоврядування.
Полікультурна компетентність
1.Використання інформації з історії математики .
2.Розв’язання задач, які підтверджують досліди та відкриття вчених-математиків.
3.Розв’язання задач історико-культурного змісту.
5.Розв’язання задач екологічного змісту.
6. Проведення інтегрованих уроків.
7. Виховання учнів на прикладі життєвого та творчого шляху видатних математиків.
Комунікативна компетентність
- Стимулювання вміння учнів висловлювати власну точку зору.
- Сприяння удосконаленню вмінь внести навчальний діалог.
- Використання усних та письмових, рецензій на відповідь,доповнень та зауважень до неї.
- Удосконаленя вмінь дітей формувати цілі власної діяльності та робити висновки за її результатами.
- Коментуваня учнями розв’язаних ними задач.
- Застосування взаємоопитування та взаємоперевірки з можливим подальшим коментуванням.
- Організація групової роботи.
- Проведення нестандартних уроків,уроків-змагань,КВК,уроків-судів.
- Проведення захистів робіт.
- Стимулювання спілкування учнів з ровесниками та дорослими з метою підвищення рівня навчальних досягнень та ерудиції учнів .
- Підготовка учнями нестандартних запитань однокласникам та вчителям.
- Організація шкільного лекторію,випуску радіогазет,усних журналів,з метою популяризації математики,як предмету.
- Забезпечення толерантного спілкування учнів у процесі роботи на уроці та позакласних заходах.
Інформаційна компетентність
1. Залучення вчителем додаткової інформації в процесі викладання математики.
2.Стимулювання учнів до використання додаткової інформації.
3. Створення в кабінеті відеотеки.
4. Активна співпраця з кабінетом інформатики щодо використання можливостей Інтернету та опрацювання навчальних програм.
5. Висвітлення значення навчального експерименту як джерела наукової інформації.
6. Використання малюнків,таблиць,схем,як джерел інформації та передбачення складання схем,таблиць,планів,опорних конспектів як результату роботи учнів з інформацією.
7. Навчання дітей співвідношенню інформації про математичні задачі з конкретними життєвими ситуаціями.
8. Навчання дітей інформаційному прогнозуванню.
Компетентність самоосвіти і саморозвитку
- Написання учнями повідомлень, рефератів, самостійних творчих робіт.
- Використання експериментальних завдань з поясненням та обґрунтування учнівських результатів,виступи на конференціях.
- Використання випереджальних завдань, що передбачають активну самоосвітню та самостійну діяльність учнів.
- Залучення учнів до роботи в МАН.
- Консультація учнів з питань самоосвіти.
- Організація інтелектуальних конкурсів,ігор,предметних тижнів,які передбачають самостійне опанування учнями певних питань та їх самоосвітню діяльність.
- Використання інтенсивних завдань з предмета,які передбачають пояснення учнями певних питань.
- Використання навчальних програм з метою самоосвіти учнів.
- Залучення учнів до роботи консультантами,що підтримує їх самоосвітній тонус.
- Поради щодо пізнавальних видань,телевізійних передач,навчальних програм,літератури тощо,як засобів для самоосвіти.
Компетентність продуктивної робочої праці
- Забезпечення високого наукового рівня викладання математики.
- Використання творчих завдань.
- Створення проблемних ситуацій на основі сучасного життя.
- Розв’язання задач різними способами,використання задач підвищеної складності.
- Складання та розв’язання учнями тестів,задач.
- Залучення учнів до участі в конкурсах «Кенгуру»
- Залучення учнів до участі в олімпіадах,МАН, у роботі заочних фізико-математичних шкіл,тощо.
- Залучення учнів до розробки та участі в заходах предметних тижнів творчого характеру.
II.Нестандартний урок як шлях формування компетентності учнів
2.1 Урок як основна форма організації навчання.
Основною організаційною формою навчання в сучасній школі є урок.
Урок — форма організації навчання, за якої заняття проводить учитель з групою учнів постійного складу, одного віку й рівня підготовки впродовж певного часу й відповідно до розкладу.
Урок має такі особливості:
- є завершеною та обмеженою в часі частиною навчального процесу, під час якого розв'язуються певні навчально-виховні завдання;
- кожен урок включається в розклад і регламентується в часі та за обсягом навчального матеріалу;
- на відміну від інших форм організації навчання є постійною формою, що забезпечує систематичне засвоєння учнями знань, умінь і навичок;
- відвідування уроків обов'язкове для всіх учнів, тому вони вивчають систему знань, поділених поурочно, в певній логіці;
- є гнучкою формою організації навчання, яка дає змогу використовувати різні методи, організовувати фронтальну, групову та індивідуальну навчальну діяльність учнів;
- спільна діяльність учителя й учнів, а також спілкування великої сталої групи учнів (класу) створює можливості для згуртування колективу дітей;
- сприяє формуванню пізнавальних якостей особистості (активності, самостійності, інтересу до знань), а також розумовому розвитку учнів.
У дидактиці існує кілька підходів до класифікації уроків залежно від ознак, узятих за основу. За способами проведення виділяють уроки-лекції, уроки-бесіди, уроки-диспути, уроки самостійної роботи учнів та ін. За етапами навчальної діяльності — вступні уроки, уроки первинного ознайомлення з матеріалом, уроки формування понять, виведення законів і правил, уроки застосування знань на практиці, уроки повторення й узагальнення матеріалу, контрольні уроки, комбіновані уроки.
Найбільш вдалою в сучасній теорії та практиці навчання є класифікація, в основу якої покладено дидактичну мету і місце уроку в загальній системі уроків (Б. Єсипов, М. Махмутов, В. Онищук). Перебуваючи на однакових позиціях, ці автори пропонують різну кількість типів уроків. За класифікацією В. Онищука розрізняють такі типи:
- урок засвоєння нових знань;
- урок формування вмінь і навичок;
- урок застосування знань, умінь і навичок;
- урок узагальнення і систематизації знань;
- урок перевірки, оцінювання та корекції знань, умінь і навичок;
- комбінований урок.
Кожен тип уроку має свою структуру, тобто склад (з яких елементів або етапів складається), послідовність (в якій послідовності ці елементи входять у заняття), зв'язок (як вони пов'язані між собою).
Визначаючи структуру уроку, вчитель повинен враховувати тему і зміст, найдоцільніші методичні засоби і прийоми, конкретні умови, в яких проводитиметься урок, рівень підготовленості учнів тощо.
Вдосконалення уроку відбувається за такими аспектами:
а) різноманітність видів уроків (урок ділова гра, урок прес-конференція, урок КВК, урок-змагання, урок-консиліум, урок-твір, урок-винахід, урок-залік та ін.);
б) максимальна щільність уроку;
в) насиченість уроку різними видами пізнавальної діяльності;
г) запровадження самостійної діяльності в роботі учнів; ґ) використання програмованого і проблемного навчання;
д) здійснення міжпредметних зв'язків;
е) подолання перевантаженості учнів.
Цікавими для теорії і практики є власне нестандартні уроки. Суть їх полягає в такому структуруванні змісту і форм, яке викликало б насамперед інтерес в учнів і сприяло їхньому оптимальному розвитку і вихованню. До нестандартних уроків слід віднести інтегровані, міжпредметні, театралізовані, сугестопедичні, уроки з різновіковим складом ; учнів та інші.
Інтегрованими називаються уроки, мета яких — подати матеріал кількох тем блоками .Міжпредметні — уроки, які ставлять за мету "спресувати" споріднений матеріал кількох предметів. Театралізовані уроки проводяться в умовах чинних програм і відведеного навчальним планом часу. Вони викликають емоції, збуджують інтерес до навчання, спираючись переважно на образне мислення, фантазію, уяву учнів. Сугестопедичні уроки ще досить рідкі, тому що механізми дії підсвідомого поки технологічно не розроблений щодо педагогіки та окремих методик. Уроки з різновіковим складом учнів мають на меті подати блоками матеріал одного предмета, що за програмою вивчається у різних класах.
Нестандартні уроки руйнують застиглі штампи так званих "зунів" (знання, уміння, навички).Структура нових типів уроків також відмінна від традиційних.
2.2 Підготовка до уроку
Підготовка вчителя до уроку
Успіх уроку значною мірою залежить від підготовки до нього вчителя. Така підготовка складається з двох етапів: попереднього і безпосереднього.
Потребує глибокого продумування кожного його структурного елемента і може відбуватися в такій послідовності:
Формулювання мети і завдань уроку. Мета уроку має бути: освітня — домогтися міцного засвоєння знань, формування практичних умінь і навичок з конкретного навчального матеріалу; розвиваюча — розвивати мовлення, пам'ять, увагу, уяву мислення, спостережливість, активність і самостійність учнів, прищепити їм способи пізнавальної діяльності та ін.; виховна — сприяти формуванню наукового світогляду, моральних, естетичних та інших якостей особистості кожного школяра, вихованню колективу класу.
Визначення обсягу і змісту навчального матеріалу. Опрацьовуючи програму, підручник і посібники, визначають провідні положення та ідеї і практичний матеріал для їх розкриття. Слід окреслити внутрішньоредметні та міжпредметні зв'язки, підібрати нові факти, приклади для наповнення теми новим змістом. Цей матеріал повинен мати належний виховний потенціал, сприяти формуванню навичок практичної роботи, розвивати інтереси і здібності учнів.
Вибір форм організації навчання. Підібравши тип уроку, слід попрацювати над раціональною його структурою, визначити тривалість кожного її елемента. Важливо продумати можливість поєднання на уроці фронтальної, групової, парної та індивідуальної роботи.
Вибір методів і прийомів навчання. Потрібно намітити, які методи використовуватимуться на кожному етапі уроку, їх поєднання, взаємодоповнення, виходячи з потреб максимальної пізнавальної діяльності учнів. При цьому слід зважати на: провідні мотиви, інтереси учнів до предмета, ставлення їх до уроків учителя; рівень сформованості вміння навчатися, працездатність, регулярність навчальної праці, виконання домашнього завдання; активність на уроках, уважність і дисциплінованість учнів; їх уміння застосовувати знання на практиці; здібності, потенційні можливості кожного.
Наочно-технічне оснащення уроку. Вчитель визначає, яку наочність або технічні засоби навчання і як буде використано на уроці.
Визначення змісту й методики виконання домашнього завдання. Обсяг домашнього завдання має бути таким, щоб не перевантажувати учнів. Учитель повинен продумати зміст інструктажу щодо його виконання.
2.3Нестандартний урок як форма організації навчання.
Головною в роботі вчителя стала проблема зробити навчання цікавим: для учня це »означає посильним і успішно-результативним, для вчителя — радісним. Творчо працюючи, він завжди прагне:
1) Пропонувати посильний рівень вимог відповідно до рівня навченості та научуваності;
2) Вчити учнів концентруватися та максимально викладатися в обмежений час;
3) Датиможливість навіть слабкому учневі отримати високу оцінку;
4) Створювати умови для свідомого і самостійного вибору учнями рівня засвоєння навчального матеріалу;
5) Дати можливість сильним учням проявити свої творчі здібності.
Адже інтерес до діяльності має спеціальну здатність підвищувати працездатність, включаючи увагу. Підтримання бажання вчитися вимагає зміни способів і форм сприйняття нового, створення різних ситуацій для застосування вивченого. Виховання І ж інтересу передбачає реалізацію багатьох методичних прийомів, пошук і застосування різних технологій навчання, а головне — невтомну вчительську працю, самовдосконалення і самоосвіту.
Систему своїх уроків треба намагатися побудувати так, щоб учні працювали з повною віддачею сил, з інтересом. Школярам подобаються завдання творчого характеру, які розвивають у них пізнавальний інтерес: складання казок, кросвордів, ігор; виконання творчих робіт; участь у математичних змаганнях. Готуючись до уроків, учитель повинен дотримуватися таких правил:
1)Урок має бути продуманим до дрібниць, щоб його етапи логічно випливали один з одного, а учні розуміли, чому, що і за чим вони роблять на занятті.
2)Корисно діяти за принципом «Краще один раз побачити, ніж сто разів почути». Усе, що вчитель говорить, бажано втілювати в зримі образи. Наочність має бути динамічною, щоб показати невидиме: хід міркувань, зв'язок між поняттями.
3) Учнів потрібно ретельно готувати до усвідомлення теми уроку, а не записувати її наперед.
4)На уроці повинно бути цікаво. Адже без емоцій, без переживань розум не напружується. Зацікавленість виникає там, де вчителю вдається захопити дітей своєю емоційністю.
Для нестандартних уроків характерною є інформаційно-пізнавальна система навчання - оволодіння готовими знаннями, пошук нових даних, розкриття внутрішньої сутності явищ через диспут, змагання. На цьому уроці вчитель може організувати діяльність класу так, щоб учні в міру можливості працювали самостійно, а він керував цією діяльністю, забезпечуючи її необхідними матеріалами. Порівняно із звичайним,
Нормативним заняттям нестандартний урок максимально стимулює пізнавальну активність та ініціативу школярів. Навчання на ньому спрямоване на підвищення якості їхніх знань, формування працьовитості, цілеспрямованості, потрібних у житті навичок і вмінь. Крім цього такі уроки більше подобаються учням, ніж буденні навчальні заняття. Насамперед тому, що навчальний процес тут має багато спільного з ігровою діяльністю дітей. Майже всі прийоми, способидії нестандартних уроків відзначаються ігровим спрямуванням. Не дивно, що в методичній літературі їх часто визначають як «урок-гра», «урок-змагання» то

2.4. Розробка й проведення уроку-казки та уроку-гри
Одним з видів нетрадиційного уроку є урок-казка. Такий урок треба проводити, використовуючи казкових персонажів, героїв мультфільмів, кінофільмів. Але казку можна написати і вибрати казкових героїв самим, спираючись на той матеріал, що вивчається у класі.
Уроки-казки супроводжуються кольоровими ілюстраціями, різнобарвними картинками, які викликають в учнів естетичні емоції, відчуття краси математики. Казки та ілюстрації до них інколи виготовляють самі учні. Іноді як домашні завдання на вихідні або на канікули пропоную написати математичну казку школярам, бо казка допомагає сформувати уяву. Особливо це важливо в 5 та 6 класах у процесі підготовки до вивчення геометрії. Крім того, на уроках, на яких знаходиться час для казки, завжди панує парний настрій, а це - запорука продуктивної праці.
Урок-гра у багатьох учнів підвищується інтерес до навчального предмету. Навіть пасивні на уроках діти хочуть вступити в гру. Ігри повніше реалізують підготовку учнів до практичної діяльності, привчають до колективних форм роботи.
Ефективною є гра, що проводиться з настановою на перемогу. Система підбиття підсумків гри передбачає:
- доброзичливе ставлення до учня;
- позитивне оцінювання зусиль учня;
- конкретні вказівки, спрямованні на покращення досягнутого результату.
Рухливі ігри, нестандартні завдання запобігають перевтомленню, підвищують працездатність, сприяють фізичному розвитку, формує в них конкретні уявлення. Полегшує оволодіння абстрактними поняттями.
Ігри розвивають мислення, кмітливість, збагачують увагу учнів, спонукають їх до пошуку, активізують клас під час вивчення нового і закріплення вже вивченого матеріалу. Гра — творчість, гра — праця. У процесі гри в дітей виробляється звичка зосереджуватися, мислити самостійно, розвивається потяг до знань. Захопившись, учні ( не помічають, що вчаться, — пізнають, запам'ятовують нове, орієнтуються в незвичних ситуаціях, поповнюють запас уяв, понять, розвивають фантазію, зорову пам'ять). Навіть найпасивніші з учнів включаються в гру з великим бажанням, докладаючи зусилля, щоб не підвести товаришів по грі. Процес гри, її результати часто спонукають деяких учнів замислитися, які прогалини є в їхніх знаннях та як їх ліквідувати.
Під час гри учні, допомагаючи один одному, значною мірою самостійно набувають нових знань. Але необхідно уважно стежити за збереженням інтересу школярів до гри, бо засоби і способи, які підвищують емоційне ставлення до гри, впливають на виконання дидактичного завдання. При цьому математичний аспект гри виводиться на перший план. Лише тоді гра виконуватиме свою роль у математичному розвитку учнів і
вихованні їхнього інтересу до математики. Підтримуючи інтерес до гри, до предмета математики, одні й ті самі етапи гри треба варіювати.
, У багатьох іграх в основу покладено принцип змагання, який підсилює емоційний характер уроку. Кращі результати гра приносить, коли змагання відбувається між командами, а мотив змагання виражається в назві гри. Наприклад: «Математичний футбол», «Брейн-ринг», «КВК»
Додаток А) Урок-гра
Тема. Додавання та віднімання звичайних дробів 5 однаковими знаменниками.
Мета: формувати в учнів навички виконання цій віднімання та додавання дробів з однаковими знаменниками; розвивати обчислювальні навички, кмітливість і старанність.
Тип уроку. Урок формування вмінь і навичок.
Учитель. Дорогі діти! Зараз ви перебуваєте у казковій країні Знань. У цій країні є міста з дивними назвами: Українська мова, Історія, Образотворче мистецтво та інші малі і великі міста. Серед них і місто Математика. Тут ви буваєте часто. У цьому місті є широкі просторі вулиці з незвичними назвами, казкові будинки, храми, величні загадкові замки. Наприклад, найвеличніший стародавній храм, у якому ви часто буваєте, називається Таблиця множення.
У місті Математика є дуже довга вулиця — вулиця Натуральних чисел. Недавно ви потрапили на нову вулицю — вулицю Дробових чисел. У першому будинку цієї вулиці живуть Звичайні дроби. Це дуже дивні чоловічки двох видів: в одних голова більша за тулуб, в інших — навпаки. Ви подружилися з ними і тепер разом сміливо заходите у кожний будинок вулиці Дробових чисел. Зараз завітаєте до будинка під вивіскою «Додавання та віднімання звичайних дробів». Фойє будинка прикрашене гаслами, на яких золотими літерами нашито правила стислою і лаконічною математичною мовою. Галілео Галілей казав: «Природа розмовляє мовою математики». Сформулюйте і ви правило додавання та віднімання дробів з однаковими знаменниками мовою математики!
(Учні формулюють правило і записують його мовою математики.)
Учитель. Ось ми бачимо на дверях однієї з кімнат вивіску «Усна лічба». Заглянемо в кімнату і виконаємо усно такі вправи:
-
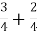 2)
2)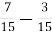
5)![]() 6)
6)![]()
7)![]() 8)
8) ![]()
9)![]()
III. Гра «Ланцюжок».
Учитель. Переходимо в іншу кімнату — ігрову. Нас запрошують пограти в гру «Ланцюжок». На першу парту кожного ряду я кладу аркуш паперу, на якому написано вправи на додавання і віднімання дробів з однаковими знаменниками. Кожен учень виконує лише одну впарву і, записавши результат, передає аркуш іншому, поки аркуш не дійде до останнього учня, який передає його учителю. Який ряд перший виконає все завдання, той і переможе.
Завдання для гри «Ланцюжок»
1)![]() 2)
2)![]()
3)![]() 4)
4)![]()
5![]() 6)
6)![]()
7)![]() 8)
8)![]()
9)![]() 10)
10)![]()
Учитель. Переходимо до іншої кімнати з вивіскою «Рівняння». Вам слід розв'язати рівняння:
Один учень з кожного ряду розв'язуватиме рівняння на дошці. Решта учнів виконуватимуть те саме завдання, що і їх представник, і матимуть право доповнювати, виправляти його. Який ряд перший -виконає всі три завдання — той і переможе.
- Цікава задача.
Учитель. Перед нами кімната з вивіскою «Цікава задача». При вході стоїть чоловічок і перевіряє всіх на уважність. Щоб розв'язати задачу, потрібно дуже уважно прочитати її умову. Якщо учень неуважний, то він не зрозуміє умови задачі, а отже, не розв'яже її. Послухайте уважно умову задачі і розв'яжіть її.
Задача. «Ішов Кіндрат у Ленінград, а назустріч йому — 12 хлоп'ят. У кожного в руках кошик, у кожному кошику — кицька, у кожної кицьки — 4 кошеняти, у кожного кошеняти в зубах по одному мишеняті. І задумався Кіндрат: «Скільки кошенят і мишенят хлоп'ята несуть у Ленінград?» (Учні відповідають. Якщо ніхто не розв'яже задачу, то вчитель продовжує цитувати Корнія Чуковського: «Ох і невдаха цей Кіндрат. Він один ішов у Ленінград, а хлоп 'ята з кошенятами і мишенятами йшли назустріч йому».)
Прикладна задача.ЗIполя зібрали по 416 ц/га буряків,зII поля зібрали - ![]() від усієї кількості ,а з III – в середньому половину від того,що зібрали з I. Яка врожайність буряків в цілому?
від усієї кількості ,а з III – в середньому половину від того,що зібрали з I. Яка врожайність буряків в цілому?
Відвідування магазину.
Учитель:Зайдемо до магазину . Тут продаються картки з вправами трьох видів :найдорожчі,середні і дешеві. Кожен учень купує їх,зважаючи на свої можливості. Ці картки не прості,а чарівні.Розв’язавши вправи ,написані на них ,учень одержує валюту,тобто знання.Після чого він може купити дорожчу картку,а отже,одержати ще більше знань.(Учитель добирає для цього етапу завдання залежно від рівня знань і вмінь учнів)
Самостійна робота.
Учитель.Заключним етапом уроку є відвідування кімнати «Самостійна робота».Ви працюватимете над виконанням диференційованих завдань,занисаних на картках.
Картка 1.
Високий рівень
1)Обчислити:
а)![]()
б)![]()
в)![]()
2)Розв’язати рівняння: ![]() -
-![]()
Картка 2
Достатній рівень
- Обчислити:
а)![]() -
-![]() +
+![]()
б)![]()
в)![]() -
-![]()
2)Розв’язати рівняння.
![]()
Картка 3
Середній рівень
1)Обчислити:
а)![]()
б)![]()
в)![]()
2)Розв’язати рівняння
![]()
Додаток Б) Урок-подорож
Тема. «Подорож математичним океаном». Розв’язування задач і вправ
Мета: освітня: вдосконалювати вміння учнів знаходити корінь лінійного рівняння з однією змінною та розв’язувати текстові задачі на складання лінійних рівнянь; розвиваюча: розвивати логічне мислення, культуру математичної мови і записів; виховна: виховувати самостійність, інтерес до математики, взаємодовіру.
Тин уроку: урок-подорож.
Обладнання: картки самоконтролю, піктограми настрою, роздавальний матеріал, плакати з умовами задач, правила проведення інтерактивної вправи «Мозкова атака» (пам’ятка). Епіграф уроку:
Вчитись можна тільки весело...
Щоб перетравлювати знання,
потрібно поглинати їх з апетитом.
А. Франс
І.Організаційний момент
Повідомлення теми, мети уроку
Відомий французький письменник XIX ст. Анатоль Франс одного разу зауважив: «Вчитися можна тільки весело... Щоб перетравлювати знання, потрібно поглинати їх з апетитом». Ці слова ми візьмемо за епіграф нашого уроку, на якому ви не просто зможете пригадати матеріал з теми «Лінійні рівняння із однією змінною», але й цікаво, я сподіваюсь, проведете час.
Під час уроку я хочу стежити за емоційним станом класу. Для цього ви маєте спеціальні «піктограми настрою»:
— гарний настрій; — середній настрій; — поганий настрій.
Сьогодні ми з вами вирушаємо у захоплюючу подорож математичним океаном. Для цієї подорожі нам потрібний корабель та екіпаж корабля: капітан, штурман і боцман. Давайте проголосуємо, хто в класі найкраще підходить для цих ролей. Капітану я вручаю карту. На ній помічено острівці й порти. Маршрут складний, нам можуть зустрітися підводні рифи, айсберг, мілина, можуть захопити в полон пірати, може трапитися шторм. Сподіваюся, що ці перешкоди не зіб’ють вас з дороги. Але, щоб взяти участь у подорожі, слід придбати путівки, вартість яких визначається не грошима, а вашими знаннями.
- Аукціон розпродажу путівок
За правильну відповідь учні отримують путівку — лист самоконтролю.
- Дайте означення рівняння.
- Яке рівняння називається лінійним? Наведіть приклади.
- Що називається коренем рівняння? Наведіть приклади.
- Скільки коренів може мати рівняння? Наведіть приклади.
- Що означає розв’язати рівняння?
- Які рівняння називаються рівносильними? Наведіть приклади.
- Назвіть основні властивості рівняння.
- Що таке математична модель задачі?
- Які задачі називаються прикладними? Наведіть приклади.
- Що спочатку треба зробити, перш ніж почати розв’язувати текстову задачу складанням рівняння?
- Що треба зробити після того, як ми розв’язали рівняння, що відповідає умові задачі?
- Який основний принцип розв’язування задач на рух?
Ви довели, що можете вирушати в подорож. Тож відпливаємо!
На дошці відкриваються пари рівносильних рівнянь, у записі яких допущені помилки. Учні знаходять їх і виправдають.
Х+41=82 2х+20=82 5х=50 2х=20
6х = 36 і х = 7; і ; і ; і ;
Капітан. Штурмане, що у нас по курсу?
Штурман. Капітане! Ми наближаємося до підводних рифів! Тривога! Капітан. Спокійно! Ми обминемо їх.
Учитель. Кожен із рифів у нашому математичному океані — це рівняння. Розв’язати рівняння правильно — означає оминути риф. Учитель роздає картки із завданням.
Учні об’єднуються у три групи навколо капітана, боцмана і штурмана (відповідно до їх навчальних досягнень) і розв’язують рівняння.
Завдання групі боцмана (середній рівень)
![]()
Завдання групі штурмана (достатній рівень)
![]()
![]()
Завдання групі капітана (високий рівень)
![]()

![]()
- Хвилинка-веселинка
У ч и т е л ь. Ви молодці! Ми благополучно оминули підводні рифи і тепер можемо відпочити та повеселитися.
Учні заздалегідь приготували усмішки і тепер зачитують.
- Скільки тобі років? Одинадцять. Та ж тобі в минулому році було тільки 5, отже, тепер має бути 6! Усе правильно. У минулому році 5, у цьому — 6, а разом 11.
-
Скільки учнів у вашому класі? З учителькою 24. А без учительки? А без учительки всі розбіжаться.
- «У полоні в піратів»
Боцман. Капітане! Поки ми веселилися й втратили пильність, нас захопили в полон пірати. Вони вимагають, щоб ми дізналися, яка їх кількість, інакше погрожують не випустити нас з полону.
Капітан. Звертаюся до вас усіх. Допоможіть розв’язати задачу, яку задали пірати. Я спробував сам угадати, скільки ж всього піратів, і сказав їм: «Добрий день, 60 піратів!» Але їхній ватажок Однооке Здоровило відповів:
«Нас не 60. Нас було б 60, якби нас було стільки, скільки зараз, і ще раз стільки, і ще півстільки, і чверть стільки, і п’ята частина стільки, та ще й коли б ти був піратом. То скільки ж нас?»
Розв’язання
![]()
![]()
![]()
![]()
![]()
![]()
Отже, піратів було 20.
Капітан. Ура! Ми знову вільні!.
Штурман. Але радіти ще рано, море неспокійне — наближається шторм.
Учитель. Не будемо чекати, поки шторм атакує нас. Атакуймо його першими.
Інтерактивна вправа «Мозкова атака»
До дошки прикріплюється плакат з умовою задачі:
Пароплав, на якому ми знаходимося, пройшов відстань від пристані А до пристані В зі швидкістю 12 км/год., а від пристані В до пристані С зі швидкістю 15 км/год. Відомо, що відстань АВ менша відстаніВСна 10 км. Знайдіть відстані між портами, в яких ми побували, якщо від В до С ми рухались на 8 хв. довше, ніж від А до В.
Учитель заохочує до обговорення побудови рисунка до умови задачі, вибору основного невідомого, складання та перевірки рівняння за умовою задачі якомога більше учнів. Приймаються абсолютно всі ідеї, жодна ідея не критикується і не відкидається. Всі ідеї затасуються на великому аркуші паперу, прикріпленому в центрі дошки. Під час обговорення кількість ідей повинна перейти в якість та правильне прокоментоване розв’язання задачі.
Ось і закінчилася подорож. Про ваш емоційний стан я можу судити з піктограм настрою. А тепер я хочу почути, що вам сподобалось на сьогоднішньому уроці, а що можна змінити на краще.
Учитель пропонує учням перелік запитань:
— Що ми робили на уроці?
- Що нового ми навчилися на сьогоднішньому уроці?
- Навіщо ми це робили?
- Чи досягай очікуваних результатів?
- Чи сподобався вам спосіб проведення сьогоднішнього уроку?
- Що сподобалось особливо під час уроку? Що не сподобалось?
- Що могло бути організовано краще, корисніше?
Учні спочатку говорять про позитивне в занятті («плюс»), а потім про моменти, які можна замінити, включаючи роботу своїх товаришів. Цей метод навчає їх дипломатично висловлювати свою думку, зважаючи на почуття оточуючих.
На початку уроку учні отримали картки самоконтролю, учитель пропонує учням заповнити їх, оцінивши свою роботу на уроці і виставити собі від 0 до 3 балів за кожний із критеріїв.
- Я допомагав(ла) іншим учням, заохочував(ла) їх до роботи.
- Я вносив(ла) вдалі пропозиції, які були враховані в ході розв’язування.
- Я активно працював(ла) у групі.
- Я узагальнював(ла) думки інших та просував(ла) роботу класу вперед.
-
Домашнє завдання
- Підготуватися до написання контрольної роботи.
- Виконати завдання.
Середній рівень
При якому значенні змінної а значення виразів 4а -10 і 3а+11 є протилежними числами? Достатній рівень
- При якому значенні змінної у значення виразу 5(7y+0,4) більше від значення виразу в 2 рази?
-
Розв’яжіть рівняння
 .
.
Високий рівень
-
При якому значенні змінної у значенім виразу
 складає половину значення виразу ?
складає половину значення виразу ?
-
Знайдіть корені рівняння
 .
.
Додаток В)
УРОК-гра
Тема. Розв’язування задач геометричного змісту
та задач на пропорційний поділ
Мета: освітня: формувати знання, вміння та навички учнів розв’язувати задачі геометричного змісту та задачі на пропорційний поділ; продовжувати формувати вміння встановлювати залежність між величинами; розвиваюча: розвивати логічне мислення та інтелектуальні здібності учнів; виховна: виховувати працьовитість, спостережливість, кмітливість.
Тип уроку: засвоєння навичок і вмінь.
Обладнання: роздавальний матеріал, правила проведення інтерактивної вправи «Мозковий штурм» (пам’ятка), кросворд.
Самоперевірка. Рівняння до задач, які пропонувалися розв’язати вдома, записані на дошці. Учні усно коментують складання і розв’язання рівнянь.
Учні повинні повторити формули для обчислення периметра і площі прямокутника і квадрата. Вони роблять це, розгадуючи кросворд, у кольоровій частині якого учні можуть прочитати закодоване слово.
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
-
Фізична величина, що обчислюється за формулою
 . (Швидкість)
. (Швидкість) 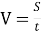
-
Чотирикутник , площу якого обчислюємо за формулою
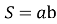 . (Прямокутник)
. (Прямокутник)
-
Площа якої фігури знаходиться за формулою
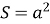 ?(Квадрат)
?(Квадрат)
-
Як називається вираз
 ? (Відношення)
? (Відношення)
- Перш ніж розв’язати прикладну задачу, ми спочатку складаємо її математичну... (Модель)
- Рівняння вигляду х-3=10 називається... (Лінійним)
- За формулою Р=2a+2b ми знаходимо периметр... (Прямокутника)
- «Розумна» машина, що вміє розв’язувати різні задачі. (Комп’ютер)
Закодоване слово — інтелект.
На попередньому уроці ми ознайомилися з принципом розв’язування задач на рух. А сьогодні ми повинні навчитися розв’язувати задачі геометричного змісту та задачі на пропорційний поділ.
Повідомлення теми і мети уроку
- Формування вмінь та навичок учнів розв’язувати задачі на складання лінійних рівнянь з однією змінною
Інтерактивна вправа «Мозковий штурм»
Після презентації умови задачі, яку необхідно розв’язати (умову краще записати на дошці) учитель пропонує всім висловити ідеї, коментарі, шляхи розв’язання. Усі пропозиції записуються на дошці чи на великому аркуші паперу в порядку їх оголошенім без зауважень, коментарів чи запитань. Необхідно заохочувати всіх до висування якомога більшої кількості ідей. У класі можна повісити плакат:
Кажіть усе, що спаде на думку. Не обговорюйте і не критикуйте висловлення інших. Розширення запропонованої ідеї заохочується
На закінченім обговорюються й оцінюються запропоновані ідеї. Учні біля дошки виконують скорочений запис задачі та розв’язують відповідне складене рівняння.
Задача 1. Периметр прямокутника 800 м. Одна зі сторін у 7 разів довша, ніж друга. Знайдіть сторони і площу даного прямокутника.
Задача 2. Одна сторона трикутника у 2 рази довша, ніж друга, і на 5 см коротша, ніж третя. Знайдіть сторони трикутника, якщо його периметр 35 см.
Задача 3. Довжини сторін двох квадратів пропорційні числам 12 і 19, а різниця їх периметрів становить 56 см. Знайдіть площу меншого квадрата.
Задача 4. Кількість однокімнатних, двокімнатних і трикімнатних квартир у будинку пропорційна числам 3; 8; 5. Скільки квартир кожного типу в будинку, якщо в ньому трикімнатних квартир на 24 менше, ніж двокімнатних?
Додаткове завдання для учнів, які навчаються на високому рівні:
— Складіть рівняння до задачі.
Периметр прямокутника 60 см. Якщо його довжину зменшити на 10 см, а ширину збільшити на 3 см, то його площа зменшиться на 96 см2. Знайдіть початкову довжину прямокутника.
Відповідь.![]() .
.
- Підсумок уроку
Заповнення листа самоконтролю.
Чи досяг я мети уроку?
Так Ні
Я працював на уроці на ___% і заслуговую оцінку___
Чи потрібна допомога під час виконання домашнього завдання?
Так Ні
- Домашнє завдання
Розв’яжіть задачі.
Середній рівень
Периметр прямокутника 16 см. Його ширина на 5 см менша, ніж довжина. Знайдіть сторони і площу прямокутника.
Достатній рівень
Довжини сторін трикутника пропорційні числам 12; 13; 19, а периметр трикутника дорівнює 220 см. Знайдіть довжини сторін трикутника.
Високий рівень
Периметр трикутника АВС дорівнює 60 см. СторонаЛВ більша від сторони АС на 5 см, а сторонаВСбільша, ніж сторона АВ на 5 см. Знайдіть сторони трикутника та визначте, яким числам вони пропорційні.
- Виставлення оцінок за урок
ЛІТЕРАТУРА
1.І.В Родигіна Компетентністно-орієнтований підхід до навчання.
2.Пометун О.І.,Пироженко Л.В..Сучасний урок.Інтерактивні теорії навчання. –2004.
3.Пєхота О.М., Любарська О.М. та ін..Освітні технології. –2004.
4.Василь Кравчук.Г.Янченко Алгебра 7 клас - 2009
5.Л.А.Губа.Нетрадиційні уроки математики. – 2005.
6.Маланюк П.М.Стежки до математичних узагальнень. – 1997.
1


про публікацію авторської розробки
Додати розробку
