Довідничок-помічничок "Означення кореня н-го степеня"
Даний матеріал допоможе повторити означення кореня н-го степеня, властивості арифметичного кореня. Матеріал містить розв'язані приклади, які допоможуть закріпити теоретичний матеріал.
Означення кореня n-го степеня.
Квадратним коренем із числа а називається число, квадрат якого дорівнює а.
Наприклад, квадратними коренями із числа 25 є числа 5 і -5. Невід’ємне значення квадратного кореня називається також арифметичним квадратним коренем. Арифметичне значення квадратного кореня із числа а позначається символом ![]() . Знак
. Знак ![]() називається знаком квадратного кореня або радикалом. Число чи вираз, що стоїть під знаком радикала, називається підкореневим числом або виразом. З означення арифметичного квадратного кореня випливає, що підкореневий вираз може набувати лише не від’ємних значень. Дію знаходження арифметичного квадратного кореня називається добуванням квадратного кореня. Дія добування квадратного кореня обернена дії піднесення до квадрата.
називається знаком квадратного кореня або радикалом. Число чи вираз, що стоїть під знаком радикала, називається підкореневим числом або виразом. З означення арифметичного квадратного кореня випливає, що підкореневий вираз може набувати лише не від’ємних значень. Дію знаходження арифметичного квадратного кореня називається добуванням квадратного кореня. Дія добування квадратного кореня обернена дії піднесення до квадрата.
Наприклад:![]() , оскільки
, оскільки ![]() ;
;
![]() , оскільки
, оскільки ![]() ;
;
![]() , оскільки
, оскільки ![]() ;
;
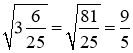 , оскільки
, оскільки 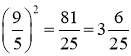 .
.
Властивість. Для будь-якого невід’ємного числа а справедливо, що ![]() і
і ![]() Наприклад:
Наприклад:![]()
Ірраціональні числа і вирази.
Якщо продовжувати добувати квадратний корінь із 2, за допомогою спеціальної комп’ютерної програми, отримаємо нескінченний неперіодичний дріб ![]()
Ірраціональним називають кожне число, яке можна виразити нескінченним періодичним десятковим дробом. Ірраціональні числа бувають додатні та від’ємні. Приклади.
![]()
Раціональні і ірраціональні числа разом утворюють множину дійсних чисел. Над дійсними числами можна виконувати арифметичні дії (ділити на нуль не можна), порівнювати дійсні числа, підносити до степеня і добувати корінь. Множину дійсних чисел позначають літерою R.
Властивості дійсних чисел:
a+b = b+a – переставна властивість додавання;
ab = ba – переставна властивість множення;
(a+b)+c = a+(b+c) – сполучна властивість додавання;
(ab)c = a(bc) – сполучна властивість множення;
a(b+c) = ac +bc – розподільна властивість.
Наприклад: ![]()
![]()
![]()
![]()
Ірраціональні вирази.
Ми розглядали раціональні вирази, з якими виконували додавання, віднімання, множення, ділення і піднесення до степеня з натуральним показником.
Вирази, які крім цих п’яти дій мають і дії добування кореня n-го степеня називаються ірраціональними виразами.
Наприклад: ![]()
 .
.
Корінь n-го степеня.
В математиці розглядають корені не тільки другого, але й третього, четвертого, п’ятої і взагалі n-го степеня.
Коренем n-го степеня з числа а, де n ϵ N, n>1, називають таке число, n-й степінь якого дорівнює а.
Наприклад: ![]() , оскільки
, оскільки ![]() ,оскільки
,оскільки ![]() оскільки
оскільки ![]()
Корінь n – го степеня із числа а позначається ![]() , читають так: корінь n-го степеня із числа а,знак
, читають так: корінь n-го степеня із числа а,знак ![]() називають радикалом. Вираз, що знаходиться під радикалом, називається підкореневим виразом, n – показник кореня.
називають радикалом. Вираз, що знаходиться під радикалом, називається підкореневим виразом, n – показник кореня.
Якщо n – непарне натуральне число, більше 1, то корінь n – го степеня з будь–якого числа існує, до того ж єдиний.
Якщо n – парне натуральне число, то корінь n – го степеня існує лише за умови , якщо ![]() Додатній корінь з числа а позначають
Додатній корінь з числа а позначають ![]() , а протилежне йому число
, а протилежне йому число ![]() якщо а=0, то існує єдиний корінь
якщо а=0, то існує єдиний корінь ![]() .
.
Отже, якщо n – непарне число, вираз ![]() має зміст при будь–якому а.
має зміст при будь–якому а.
Якщо n – парне, ![]() має зміст, якщо
має зміст, якщо ![]()
Арифметичним коренем n-го степеня з невід’ємного числа називається невід’ємне число, n-ий степінь якого дорівнює а.
Властивості арифметичних коренів.
-
Якщо
 і
і  правильна рівність
правильна рівність  .
.
Приклад: ![]() бо
бо ![]() .
.

![]() оскільки
оскільки ![]()
-
Якщо
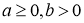 і
і  правильна рівність
правильна рівність  .
.
Приклад: ;
;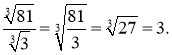
3. Якщо ![]()
![]() правильна рівність
правильна рівність ![]() .
.
Приклад: ![]()
4. Якщо![]() правильна рівність
правильна рівність ![]() .
.
Приклад: ![]()
5. Якщо ![]() правильна рівність
правильна рівність ![]()
Приклад: ![]()


про публікацію авторської розробки
Додати розробку
