Матеріал до уроку "Використання області визначення функції для розв’язування рівнянь."

Використання області визначення функції для розв’язування рівнянь.

Усе частіше в літературі зустрічаються рівняння, розв'язування яких стандартними способами важке, громіздке або неможливе. Тоді можна спробувати використовувати властивості функцій. Іноді такий підхід приводить до більш простого і раціонального розв'язання .

 У рівнянні спільна область визначення для функцій називається областю допустимих значень цього рівняння. Кожен корінь заданого рівняння входить як до області визначення функції , так і до області визначення функції . Отже, кожен корінь рівняння обов’язково входить до ОДЗ цього рівняння. Це дозволяє в деяких випадках, аналізуючи ОДЗ, одержати розв’язки рівняння. Якщо ОДЗ рівняння складається із скінченої кількості числових значень, то для розв’язання достатньо перевірити всі ці значення

Приклад 1. Розв’язати рівняння .

Розв’язання. ОДЗ можна записати за допомогою системи

тобто . Отже, ОДЗ заданого рівняння складається лише з одного значення . Шляхом перевірки встановлюємо, що корінь рівняння.

Відповідь. 2.

Приклад 2. Розв’язати рівняння .

Розв’язання. ОДЗ Якщо , то , але то для всіх значень зміної з ОДЗ .                          Відповідь: .

Приклад 3. Розв’язати рівняння .

Розв’язання. ОДЗ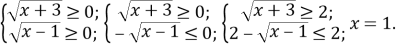

Відповідь:1.

Приклад 4. Розв’язати рівняння .

Розв’язання. , тоді і , тоді , але , тоді рівність досягається за умови рівності нулю обох частин при . Перевіркою переконуємося, що і 2 є коренями рівняння.

Відповідь:0;2.

Приклад 5. Розв’язати рівняння =

Розв’язання. Знаходимо О.Д.З.

Відповідь. ∅.