елементи комбінаторики

Елементи комбінаторики ( домашнє завдання до уроку ) Підготувала студентка 41 МЕІ Уманець М.Є. «Теорія без практики мертва та безплідна, практика без теорії неможлива чи згубна. Для теорії потрібні головним чином знання, для практики, крім того, і вміння». О.М.Крилов

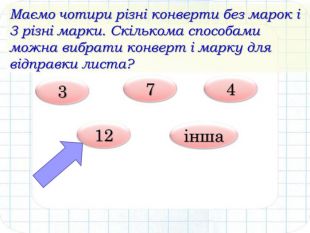
Учню треба скласти 4 екзамени протягом 8 днів. Скількома способами він може це зробити? Іншими словами нам необхідно із множини 8 днів вибрати всі можливі підмножини із 4 днів, і в кожній із вибраних підмножин розставити різними способами 4 предмети, які необхідно здати Пропоную завдання

Звичайно, у цьому вам може допомогти спосіб перебору, але відповісти строго математично на дане питання і багато інших нам допоможе розділ математики – комбінаторика. Я пропоную вам побути дослідниками вивчення даної теми. У цьому вам допоможе презентація, а також посилання у ній на інтернет - ресурси( відеоуроки, презентації, вікіпедія) ( у презентації це виділено фіолетовим кольором)

Комбінаторика — розділ математики, у якому вивчають способи вибору та розміщення елементів деякої скінченної множини на основі якихось умов. Вибрані ( або вибрані й розміщені) групи елементів називають сполуками Комбінаторика – розділ математики в якому вивчаються властивості сполук (комбінації, розміщення, перестановки) Комбінаторні задачі –задачі, в яких потрібно знайти кількість можливих способів утворення таких підмножин.

Деякими комбінаторними задачами цікавились ще математики Стародавньої Греції, пізніше ними займалися арабські математики. На початку двадцятого століття комбінаторику вважали завершеним розділом математики.

Історія виникнення комбінаторики XVI століття (азартні ігри) Н.Тарталья – італійський математик (різні комбінації під час гри) XVIІ століття Б. Паскаль, П. Ферма – французькі вчені ( теоретичне дослідження). XVIІІ століття Я. Бернуллі, Л. Ейлер – подальший розвиток комбінаторики

З комбінаторними обчисленнями доводиться мати справу представникам багатьох спеціальностей: ученому-хімікові під час розгляду можливих типів зв'язків атомів у молекулах; біологові під час вивчення можливих послідовностей чергування амінокислот у білкових сполуках; агрономові, який розглядає способи посівів на кількох ділянках; диспетчерові під час складання графіка руху тощо…

Пограємось

Розглянемо наступні задачі Проаналізуємо умови задач. Що у них спільного? Запишіть усі трицифрові числа, які можна утворити за допомогою цифр 1, 2, 3 не повторюючи їх у запису числа. Скільки таких чисел утворилось? Десять друзів зайшли перекусити до кав’ярні. Вони довго вирішували, яким чином розміститися за стійкою. Хазяїн кав’ярні запропонував їм угоду, за якою друзі можуть приходити щодня, але сідати кожного разу у різному порядку. Після того, як вони перепробують усі можливі варіанти, їх будуть годувати за рахунок закладу. На який день друзі отримають безкоштовний обід? В обох задачах ми маємо справу з деякою множиною різних елементів, для яких встановлюється певний порядок

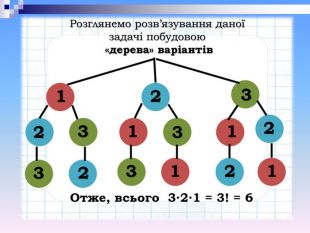
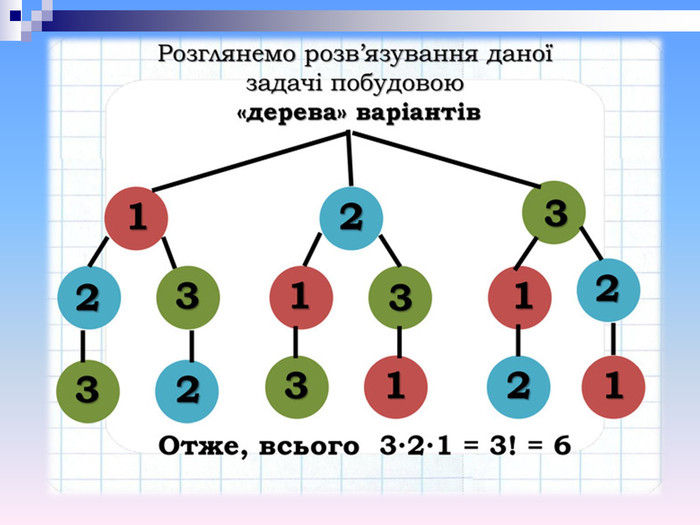
Запишіть усі трицифрові числа, які можна утворити за допомогою цифр 1, 2, 3 не повторюючи їх у запису числа. Скільки таких чисел утворилось? На перше місце можна записати будь-яку з даних цифр, тобто є 3 різні можливості. На друге місце можна записати вже будь-яку з цифр, що лишилися, тобто є 2 можливості. Кожна перша цифра може комбінуватися з будь-якою цифрою, що стоїть на другому місці. Тому загальне число різних способів запису двох цифр є 3  2 = 6. Далі вже зрозуміло, що на третє місце можна записати вже тільки одну цифру, що залишились, тому для трьох цифр кількість способів є 3  2  1 = 6. Як зміниться відповідь задачі 2, якщо цифру 3 замінити на цифру 0? Пояснити. Оскільки число не може починатися з цифри 0, то загальна кількість утворених чисел буде 2  2  1 = 4. Підказка

Десять друзів зайшли перекусити до кав’ярні. Вони довго вирішували, яким чином розміститися за стійкою. Хазяїн кав’ярні запропонував їм угоду, за якою друзі можуть приходити щодня, але сідати кожного разу у різному порядку. Після того, як вони перепробують усі можливі варіанти, їх будуть годувати за рахунок закладу. На який день друзі отримають безкоштовний обід? Припустимо, що друзі заходять до кав’ярні по одному. Перший може вибрати собі місце 10 способами, другий — 9 способами. Тому для перших двох друзів є 10 · 9 = 90 варіантів зайняти два місця. Міркуючи аналогічно і застосовуючи правило множення, отримуємо 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = = 3 628 800 варіантів. У перерахунку на роки — більше 9935 років

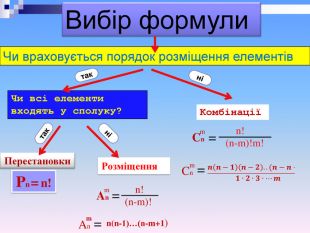
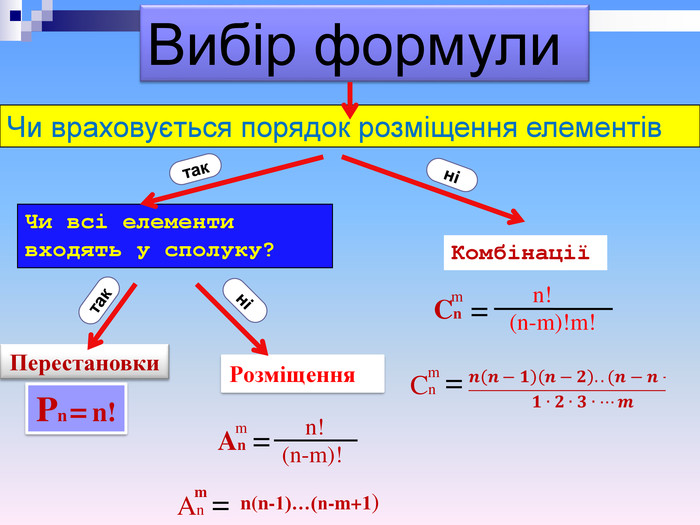
Отже, в даних задачах ми впорядковували елементи кожної із даних множин і фактично відповідали на запитання : « Скількома способами можна впорядкувати елементи множини?» В комбінаториці будь-яка впорядкована множина, що складається з n елементів називається перестановкою Усі перестановки з n елементів відрізняються одна від одної порядком розміщення цих елементів Формула для обчислення кількості перестановок

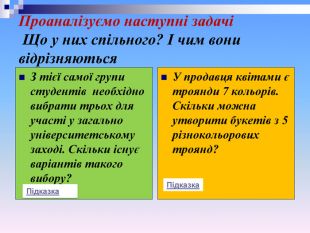
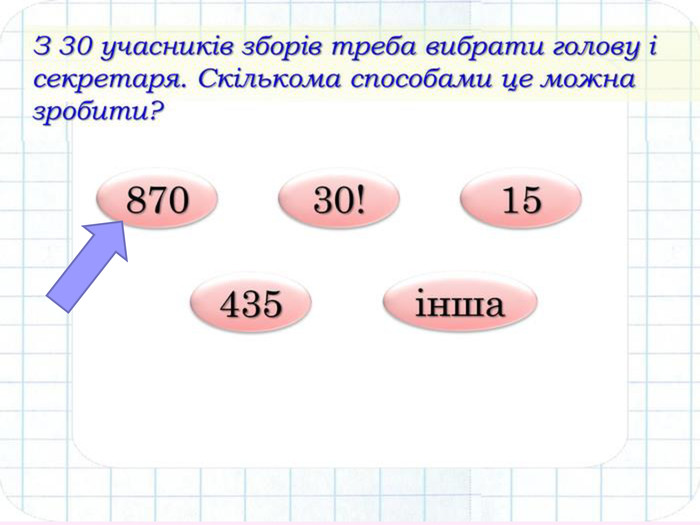
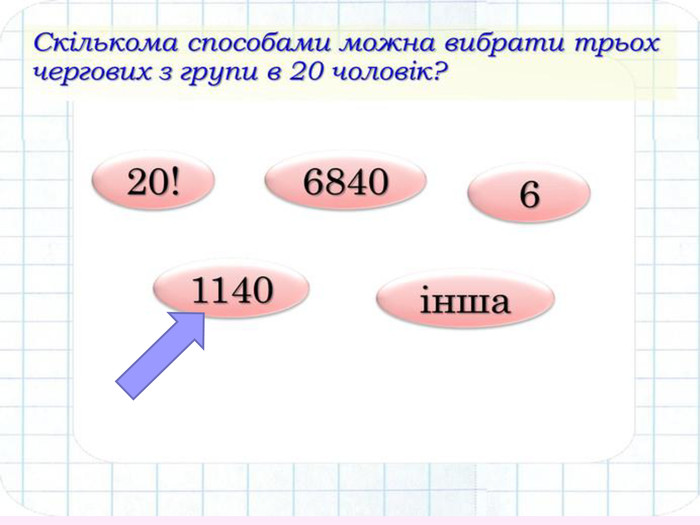
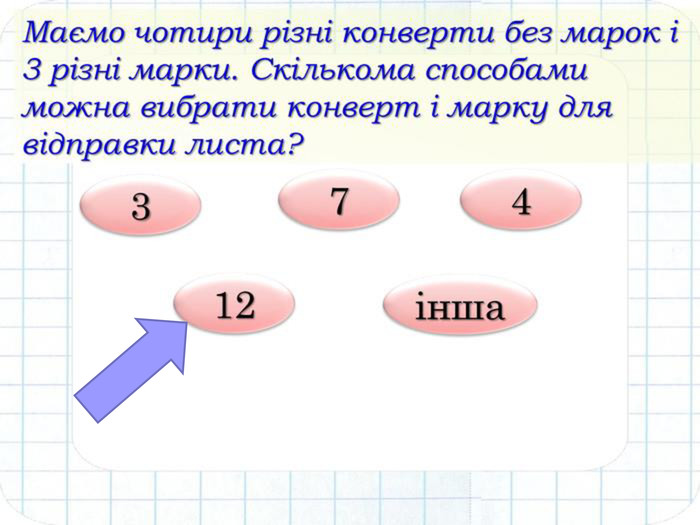
Проаналізуємо наступні задачі Що у них спільного? І чим вони відрізняються від попередніх задач? Скільки трицифрових чисел можна утворити з цифр 2, 3, 4, 7, не повторюючи цифри в запису числа? Як зміниться відповідь, якщо замість цифри 7 взяти цифру 0? З 18 студентів групи необхідно вибрати старосту, його заступника і профорга. Скільки існує варіантів такого вибору? Підказка Підказка

Знову в задачах ми мали справу з деякою множиною різних елементів. Потім ми впорядковували певну кількість елементів кожної із множин, отримували різні впорядковані підмножини розглядуваних множин і відповідали на запитання скількома способами можна впорядкувати різні підмножини даної множини Усі розміщення з n елементів по m n елементів відрізняються одна від одної складом елементів та порядком їх розташування. Формула для обчислення кількості розміщень

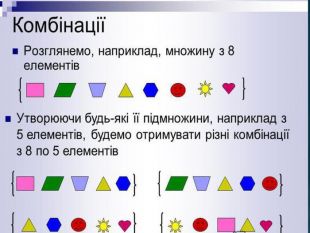
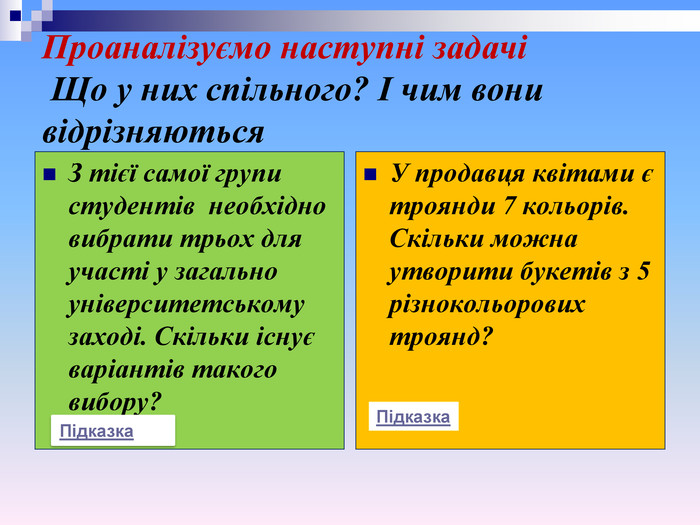
Проаналізуємо наступні задачі Що у них спільного? І чим вони відрізняються З тієї самої групи студентів необхідно вибрати трьох для участі у загально університетському заході. Скільки існує варіантів такого вибору? У продавця квітами є троянди 7 кольорів. Скільки можна утворити букетів з 5 різнокольорових троянд? Підказка Підказка

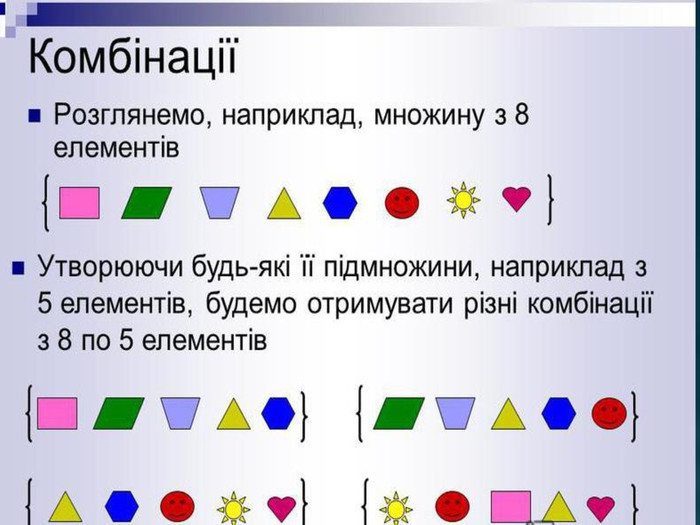
Знову у задачах ми мали справу з деякою множиною різних елементів. Потім ми вибирали певну кількість елементів кожної з множин, отримували різні,але вже не впорядковані підмножини розглядуваних множин і відповідали на запитання скількома способами це можна зробити. Усі комбінації з n елементів по m n елементів відрізняються одна від одної складом елементів Формула для обчислення кількості комбінацій

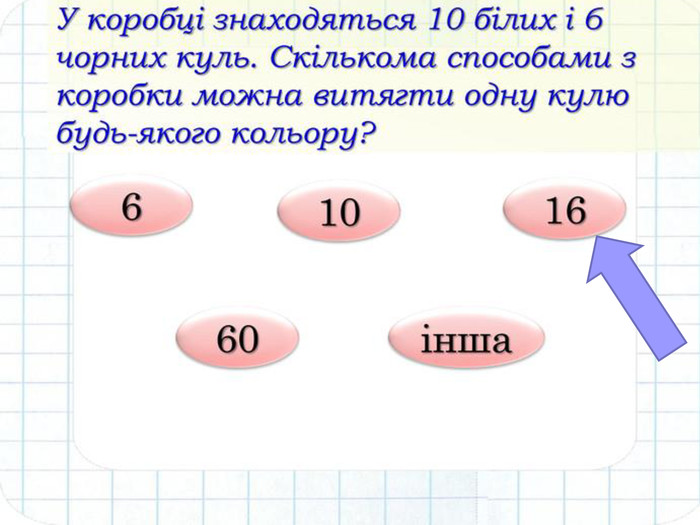
Ідучи на тренування спортсмен одягає або майку або футболку. Скільки варіантів вибору майки або футболки у нього є, якщо його мама випрала 3 майки і 4 футболки ? Припустимо, що у шафі на одній поличці лежать 3 майки, а на другій – 4 футболки. Довільно з якої-небудь полички беремо тільки одну річ. З першої полички взяти одну річ можна 3 різними способами, а з другої – 4 способами. Тоді взяти одну яку-небудь річ можна 3 + 4 = 7 різними способами.

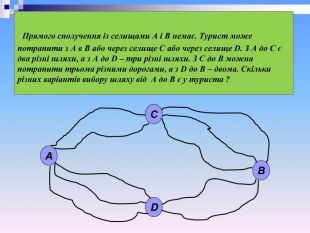
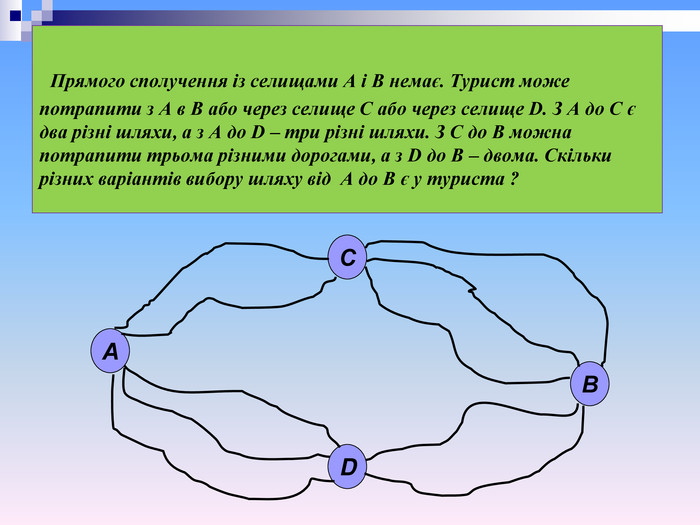
Прямого сполучення із селищами А і B немає. Турист може потрапити з А в В або через селище С або через селище D. З А до С є два різні шляхи, а з А до D – три різні шляхи. З С до В можна потрапити трьома різними дорогами, а з D до В – двома. Скільки різних варіантів вибору шляху від А до В є у туриста ? А С D В

Прямого сполучення із селищами А і B немає. Турист може потрапити з А в В або через селище С або через селище D. З А до С є два різні шляхи, а з А до D – три різні шляхи. З С до В можна потрапити трьома різними дорогами, а з D до В – двома. Скільки різних варіантів вибору шляху від А до В є у туриста ? Якщо йти з А в В через С, то за правилом множення шлях можна обрати 2 · 3 = 6 способами. Якщо йти з А в В через D , то для вибору шляху є 3 · 2 = 6 способів. Тоді різних варіантів вибору шляху за правилом додавання є 6 + 6 = 12.

Підсумуй досліджене

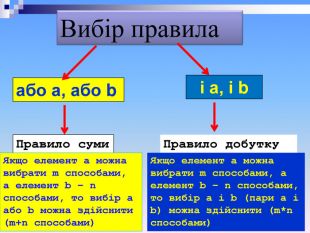
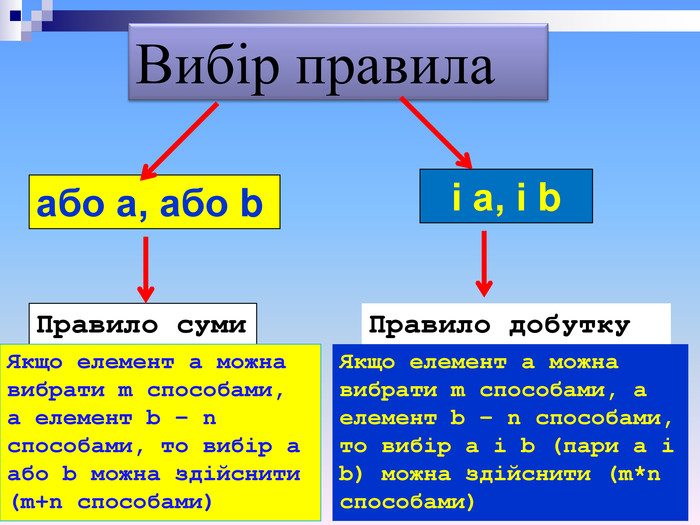
Вибір правила або а, або b і а, і b Правило суми Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а або b можна здійснити (m+n способами) Правило добутку Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а і b (пари а і b) можна здійснити (m*n способами)

Вибір формули Чи враховується порядок розміщення елементів Чи всі елементи входять у сполуку? Розміщення An m = n! (n-m)! An m = n(n-1)…(n-m+1) Комбінації Cn m = n! (n-m)!m! Cn m = Перестановки Pn = n! так так ні ні

Якщо у тебе виникли труднощі під час дослідження даної теми, корисним буде перегляд відеоуроків за посиланням Відеоурок « Елементи комбінаторики» Підготовка до ЗНО « Елементи комбінаторики» Підготовка до ЗНО « Елементи комбінаторики» Правило добутку