Кишеньковий довідник четвертокласника

 

 

 

 

 

 

 

 

 

 

 

 

 

ЦЕ  ПОВИНЕН  ЗНАТИ
КОЖЕН
четвертокласник

 

 

 

 

 

 

 

 

 

 Числові вирази та буквені  вирази  і  їх значення. Формули.

 Числовим виразом називається запис, складений із чисел, знаків арифметичних дій і дужок. Числовий вираз має лише одне значення.

Для обчислення значення числового виразу необхідно дотримуватись такого порядку дій:

- першими виконуються дії піднесення до степеня (до квадрата чи куба);

- потім виконуються дії множення і ділення;

- останніми виконуються дії додавання і віднімання.

Якщо числовий вираз містить дужки, то спершу виконуються дії в дужках.

Буквеним виразом називається запис, складений із букв, чисел, знаків арифметичних дій і дужок. Буквений вираз може мати кілька значень, які залежать від значення букв, які входять до виразу.

 

 

 

 

 

 

 

 

 

 

                                              

 

 

                                                       буквеного

 

Обчислити

значення вирвзу

                                        

                                               числового

                           

 

 

 

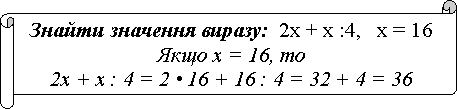
Якщо зазначені дії в виразі не можна виконати, то кажуть, що вираз не має змісту:  (а + 3) : (а –1) не має змісту при а = 1

Якщо буквений вираз позначити деякою буквою, то рівність, одна частина якої містить цю букву, а друга містить буквений вираз, становитиме формулу.

Наприклад:

1. Формула шляху

      S = v • t        s – пройдений шлях, v – швидкість, t – час;

2. Формула периметру квадрату

      Р = 4а          а – сторона квадрата, Р – периметр квадрата;

3. Формула площі прямокутника

      S = а • в      а  і  в – сторони прямокутника, S – площа;

4. Формула площі квадрата

      S = а²              а – сторона квадрата,  S – площа квадрата;

 

        Із формули можна виразити будь-яку букву, що входить до неї. Із формули пройденого шляху випливає:

1. формула швидкості: v =

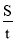
     тобто, щоб знайти швидкість, треба пройдений шлях поді-  

     лити на час руху;

2. формула часу: t  =     

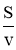
     тобто, щоб знайти час руху, треба пройдений шлях поділити 

              на швидкість руху.

                                               

                                                      1) Знайди значення числового виразу:

49 + (783 – 23) : 2³

                                                2) Знайди значення буквеного вираз:

                                           2х + у – 7,  якщо х = 5 і  у = 4

3. Купили а зощитів по 60 к. і альбом за 85 к. Скільки копійок коштує вся покупка? Напиши відповідний буквений вираз і обчисли його, якщо а = 3.
4. Автомобіль їхав зі швидкістю  а  км/год і проїхав 350 км. Скільки часу був автомобіль у дорозі, якщо  а  = 70 км/год?

 

Спрощення   виразів

    Буквені вирази можна спрощувати, застосувавши закони додавання і множення.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

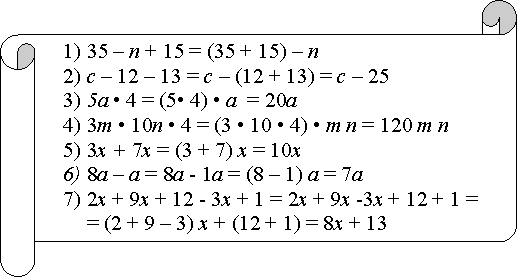
Рівняння

Рівняння - це рівність, яка містить невідоме, яке позначене буквою.

Корінь рівняння (його розв’язок) – це значення невідомого, що перетворює рівняння на правильну рівність.

Розв’язати рівняння – означає знайти всі його корені або переконатися, що рівняння не має коренів.

 

                                  Під час розв’язування рівнянь користуються                                                                                               

                            такими правилами:

                            1) щоб знайти невідомий доданок, треба від суми     відняти відомий доданок:   х + 17 = 28

                                               х = 28 – 17

                                               х = 11

2) щоб знайти невідоме зменшуване, треба до різниці додати

    від’ємник:      у – 54 = 100

                            у = 100 + 54

                            у = 154

3) щоб знайти невідомий від’ємник, треба від зменшуваного відняти                                                                                             

     різницю:        152 – к = 64             

                             к = 152 – 64

                             к =  88

4) щоб знайти невідомий множник, треба добуток поділити на відо-

    мий множник:       68 х = 136

                                    х = 136 : 68

                                    х = 2

5) щоб знайти невідоме ділене, треба частку помножити на  дільник:

             у : 11 = 11

             у = 11 • 11

             у = 121

6) щоб знайти невідомий дільник, треба ділене поділити на частку:

                200 : р = 10

                р = 200 : 10        

                р = 20

 

Кількість коренів рівняння

Рівняння може:

1) не мати коренів:   х · 0 = 1

2) мати один корінь:  х + 15 = 32  

                                     х = 32 – 15                           

                                     х = 17

3) мати декілька коренів:   (х – 3) (х – 5) (х – 10) (х – 20) = 0

                              х – 3 = 0   або х – 5 = 0   або х – 10 = 0   або х – 20 = 0

                               х =3                х =5                 х = 10               х = 20

4) мати безліч коренів:   у · 0 = 0

                                          у – любе число.

 

Розглянемо більш складні рівняння

            

 

 

 

 

 

 

 

 

 

                                                   Розв’яжи  рівняння:

1. 236 – х = 75             4) 100 : (3р + 1) = 4
2. 45 + у = 94               5)180 : 3у = 5
3. х + 5х + 12 =72       

 

 Рівняння допомагають розв’язувати задачі

Перший  тип  задач

 

 

 

 

 

Задача 1	Задача 2
У двох кишенях 12 горіхів. У другій кишені вдвічі більше горіхів, ніж у першій. Скільки горіхів у кожній кишені?	У двох кошиках 19 яблук. В одному кошику на 5 яблук менше, ніж у другому. Скільки яблук у кожному кошику?

 

           Другий  тип задач                            Третій  тип  задач

 

 

 

 

 

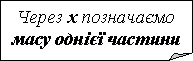
Задача 3	Задача 4
Бронза складається з 3 частин олова і 17 частин міді. Скільки олова і бронзи в бронзовій деталі масою 80 г?	Син у 4 рази молодший за батька. Скільки років батькові, якщо він старший за сина на 27 років?

 

                                                                  Розв’яжи  задачі:

1. У двох подруг Олі та Каті разом 20                   

                                                  зошитів. Скільки зошитів у кожної подруги          

                                          окремо, якщо у Олі зошитів втричі більше, ніж у Каті?

 

2.  У двох сувоях 75 м тканини. У другому сувої на 9 менше, ніж у першому. 

     Скільки метрів тканини в кожному сувої?

 

3.  Маса однієї деталі у 7 разів перебільшує масу другої. Знайди маси деталей,   

     якщо маса однієї деталі більша від другої на 12 кг.