Конспект уроку з теми "Площі фігур"

Колоквіум, 9 клас

Тема. Поняття площі.

Мета. Перевірити теоретичні і практичні навички на обов’язковому рівні у вигляді тесів і на підвищеному рівні у вигляді письмової роботи знаходити площі фігур.

Тип уроку: урок контрольно-заліковий (2 уроки).

План уроку:

1. Теоретична розминка
2. Усні вправи
3. Математичний диктант
4. Тест
5. Письмова роботаа
6. Залік 3 теорії

На урок запрошені 3 учні 11 класу. Кожний з них контролює 1 ряд.

Хід уроку:

1.     На цьому етапі учень може отримати лише штрафні бали, якщо неправильно відповість на запитання (по 2 бали).

Запитання.

1. Сформулювати властивості площі.
2. За якою формулою можна знайти площу прямокутника?
3. Як знайти площу квадрата, якщо довжина сторони а?
4. За якою формулою обчислюється форма трапеції?
5.                   Чому дорівнює площа паралелограма, якщо відомо, що довжина сторони його дорівнює а, а висота, проведена до неї – h?

2. Усні вправи (максимальна кількість – 11 балів).

Перед кожним учнем лежать картки, на яких написано: 0,1; 0,01; 0,0001; 10; 100;10000; 1000000. Для відповіді учні піднімають потрібну картку, консультанти записують бали в залікові таблиці.

Правильна відповідь – 1 бал.

Вправи.

1. 1а – це квадрат із стороною …
2. 1 га – це квадрат із стороною …
3. Скільки сантиметрів квадратних у 1 м²?
4. Скільки дециметрів квадратних у 1 м²?
5. Скільки гектарів у 1 а?
6. Скільки гектарів у 1 км²?
7. Скільки міліметрів квадратних у 1 см²?
8. Скільки арів у 1 км²?
9. Скільки арів у 1 дм²?
10.            Скільки міліметрів у 1 см?
11.            Скільки метрів у 1 дм?

3.     Диктант (максимальна кількість – 7 балів). Учні виконують завдання на окремих аркушах. Правильна відповідь на 1 запитання – 1 бал.

Запитання.

1. Записати формулу Герона.
2. За якою формулою обчислюється площа трапеції?
3. Записати формулу для обчислення площі квадрата, якщо його діагональ d.
4. Записати формулу для обчислення площі трикутника, якщо відомо довжини двох його сторін і кут між ними.
5. Записати формулу для знаходження радіуса кола, вписаного в трикутник.
6. Записати формулу для знаходження радіуса кола, описаного навколо трикутника.
7. Записати формулу для обчислення площі паралелограма, якщо відомо довжини його діагоналей і кут між ними.

4. Тест (максимальна кількість балів – 16, по 2 бали за кожне завдання).

Учні розв’язують завдання в чернетках, правильні відповіді відмічають в таблицях, які зроблено завчасно.

1. Сторона правильного трикутника 4 см. Знайти його площу.

А) 16 см²; Б) см²; В) 16 см²; Г) інша відповідь.

2. У скільки разів треба зменшити сторону квадрата, щоб його площа зменшилася у 4 рази?

А) у 8 разів; Б) у 2 рази; В) у 4 рази; Г) інша відповідь.

3) Чому дорівнюють сторони прямокутника, якщо вони відносяться як 4:9, а його площа 144 см²?

 А) 8 см; 18 см; Б) 4 см; 9 см; В) 16 см; 36 см; Г) інша відповідь.

4) Знайти площу трикутника, якщо його сторони 5 см, 5 см, 6 см.

 А) 12 см²; Б) 25 см²; 15 см²; Г) інша відповідь.

5) Знайти площу ромба, якщо його діагоналі 24 дм, 5дм.

 А) 120 дм²; Б) 60 дм²; В) 30 дм²; Г) інша відповідь.

6) Знайти радіус кола описаного навколо трикутниками із сторонами 7 см, 15 см, 20 см.

 А) 25Псм²; Б) 750 см²; В) см²; Г) інша відповідь.

7) Знайти площу трапеції рівнобічної з основами 20 см і 36 см, а бічна сторона 17 см.

А) 720 см²; Б) 340 см²; В) 420 см²; Г) інша відповідь.

8) Знайти площу трапеції із основами 25 см і 11 см, а бічними сторонами 13 см і 15 см.

А) 196 см2; Б) 252 см2; В) 216 см2; Г) інша відповідь.

5. Письмова робота (максимальна кількість – 21 бал).

Завдання записані на дошці, яка до цього часу була закрита. За кожне завдання учень одержує 7 балів учні виконують роботу в зошитах для контрольних робіт. Письмову роботу перевіряє вчитель після колоквіуму. Результати оголошуються на наступному уроці.

І варіант.

1.     У прямокутнику діагональ дорівнює d і утворює із стороною кут 30°. Визначити площу прямокутника.
2.     Сторони трикутника 15 см, 26 см, 37 см. Знайти радіус кола вписаного в трикутник.
3.     Обчислити площу рівнобічної трапеції, у якої основи 20 дм і 30 дм, а гострий кут 45°.
4.  (Необов’язкове, оцінюється окремо – 7 балів).

Обчислити площу рівнобічної трапеції, основи якої дорівнюють 12 см і 18 см, а діагоналі взаємно перпендикулярні.

ІІ варіант.

1.               Площа прямокутника S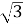. Визначити діагональ прямокутника, якщо вона утворює з однією з його сторін кут 30°.
2.     Сторони трикутника дорівнюють 16 см, 30 см, 34 см. Знайти площу круга, описаного навколо трикутника.
3.     Знайти площу рівнобічної трапеції, у якої гострий кут дорівнює 45°, менша основа 5 дм, а висота – 4 дм.
4. (Необов’язкове, оцінюється окремо – 7 балів).

Обчислити площу рівнобічної трапеції, основи якої дорівнюють 26 см і 10 см, а діагоналі перпендикулярні до бічних сторін.

Максимальна кількість балів – 55.

Оцінки:

1 ― 1-4 балів;

2 ― 5-8 балів;

3 ― 9-11 балів;

4 ―12-14 балів;

5 ― 15-17 балів;

6 ― 18-20 балів;

7 ― 21-24 бали;

8 ― 25-28 балів;

9 ―  29-33 бали;

10 ― 34-40 балів;

11 ― 41-47 бали;

12 ― 48-55 балів.

7. Підсумок урок і повідомлення домашнього завдання.

Ми вивчили  одну із найважливіших тем геометрії – площі простих фігур. Пам’ятайте про все, що ми говорили, вивчаючи цю тему, бо вона має практичне застосування у житті кожної людини.

Домашнє завдання

Обов’язковий рівень: виконати інший варіант тесту;

Підвищений рівень: виконати інший варіант контрольної роботи.