Математичний захід до тижня математики "Простори і поверхні"

Новомиколаївська загальноосвітня школа І – ІІ ст.

Простори і поверхні.

Хвилі вселяли йому, що будь-яка форма у просторі утворюється при перетині тієї чи іншої фігури з великою кількістю вимірювань. Квадрат це результат перерізу куба, а коло - перерізу сфери. Тривимірні куб і сфера виникають при перерізі фігур чотирьох вимірів, про що люди досі лише здогадувалися і що зрідка бачили уві сні. Чотиривимірні фігури створюються з допомогою перерізу п’ятимірних і так далі, аж до запаморочливої нескінченності прообразів.

Р. Ф. Лавкрафт

Зараз математика потрібна всім. Без математичних обчислень не можна побудувати не тільки космічного корабля, електростанції, підводного човна, а й звичайного будинку.

Збільшується не тільки кількість наук, які вже не можуть обходитись без математики, а й обсяг математичних знань, використовуваних цими науками.

Повертаючись до слів Лавкрофта, гадаю, ви вже зрозуміли, що мова піде про простори. Що ж таке простір?

Говорячи мовою математиків, простором називається математична множина, що має структуру, обумовлену аксіоматикою властивостей його елементів (наприклад, точок в геометрії, векторів в лінійній алгебрі, подій в теорії ймовірностей і так далі).

Виходячи з означення, бачимо, що простір не оди, він різний і існує в різних напрямах як алгебри, так і геометрії.

Наприклад: Афінний простір, Банахів простір, Ймовірнісний простір, Гільбертовий простір, Евклідовий простір, Нормований простір, Векторний простір, Метричний простір, Топологічний простір, Простір з мірою і т.д.

Але ми спробуємо розібратися з Евклідовим простором в геометрії.

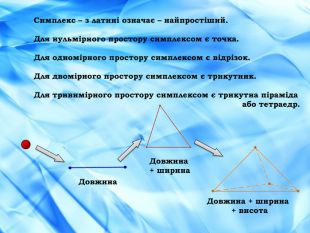
Спочатку познайомимося з таким поняттям, як «симплекс». (слайд 3).

На основі слайду   - «гра з пластиліном».

Фільм – «тур 6д». (слайд 4)

(Слайди 5-6) Думки в багатовимірному просторі висловлював І. Кант (1746), а про приєднання до простору як 4-ї координати часу писав Ж. Д'аламбер (1764). Побудову ж евклідової багатовимірної геометрії було здійснено А. Келі (1843), Р. Грассманом (1844) і Л. Шлефли (1852).

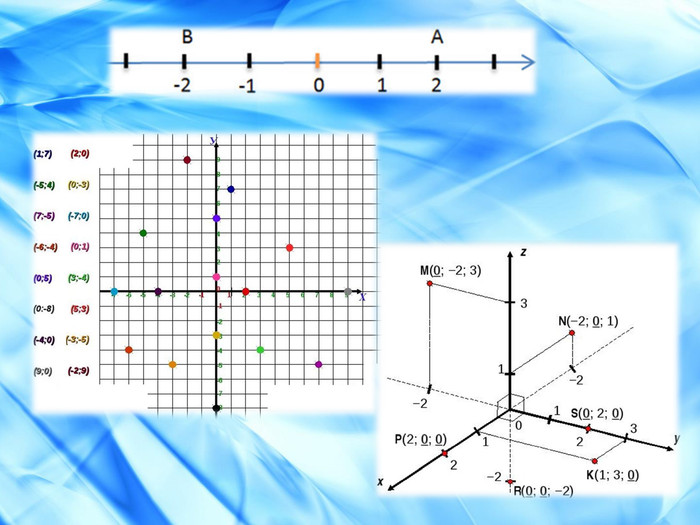
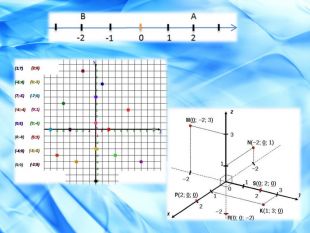
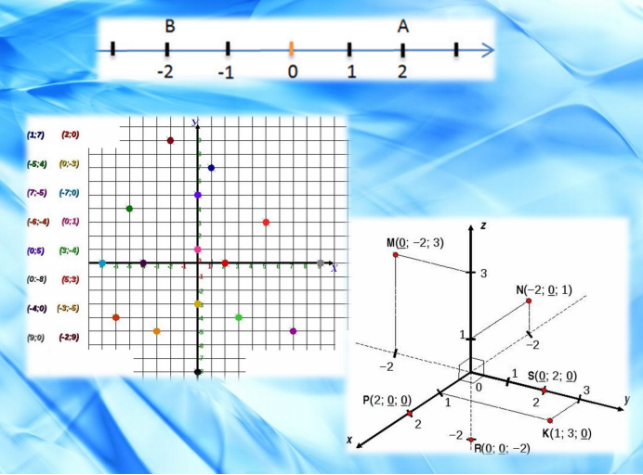
На площині кожна точка задається в системі координат двома числами – координатами цієї точки, а в просторі – трьома координатами. В n-мірному ж просторі, точка задається n координатами, тобто записується у вигляді A(x₁, x₂, ..., x_n), де x₁, x₂, ..., x_n – довільні дійсні числа (координати точки А). Система координат на площині має дві осі, в просторі – три, а в n-мірному просторі система координат містить n осей, причому кожні дві з цих осей перпендикулярні одна одній.

Побачити – в буквальному, фізичному розумінні цього слова – фігури в чотиривимірному просторі (а тим більше в просторах більшого числа вимірів) не в змозі ніхто, навіть самий геніальний математик; їх можна бачити тільки уявним поглядом.

Але математична несуперечність n-вимірної геометрії ще недостатня для судження про цінність цієї теорії.

Практично-лекційна частина. (Слайди 7-8)

Цінною для нас є інша теорія, теорія про поверхні. Перед вами смужки з паперу. Візьміть одну і склейте в кільце. Проведемо всередині лінію. Побачимо, що кільце має дві поверхні.

А тепер давайте візьмемо іншу смужку і склеїмо, перегорнувши на 180⁰. Тепер знову проведемо всередині лінію. Бачимо, що нове кільце має одну поверхню і один край. Те, що ми отримали має назву – лист Мебіуса.

Лист Мебіуса є однією з самих незвичайних геометричних фігур.

Лист Мебіуса – це тривимірна неорієнтована фігура з одним краєм і однією поверхнею. Цим він унікальний і відрізняється від всіх інших предметів, які можуть зустрітися в повсякденному житті. Лист Мебіуса також називають поверхнею Мебіуса. Вона відноситься до топологічних об'єктів, тобто об'єктів безперервним. Такі об'єкти вивчає топологія - наука, що досліджує безперервність середовища і простору.

Інтерес викликає вже саме відкриття листа. Два математики, незалежно один від одного, відкрили його в одному і тому ж 1858 році. Цими засновниками були Август Фердинанд Мебіус і Йоганн Бенедикт Лістинг. Цікаво, що обидва були учнями Карла Фрідріха Гауса.

Умовно розрізняють стрічки за способом згортання: за годинниковою стрілкою і проти годинникової стрілки. Їх ще називають права і ліва. Але розрізнити «на око» вигляд стрічки неможливо.

Деякі вважають, що ця загадкова геометрична фігура - прообраз перевернутої вісімки-нескінченності, насправді це невірно. Цей символ був введений для використання набагато раніше, ніж був відкритий лист Мебіуса. Містики називають лист Мебіуса символом подвійного сприйняття єдиного.

1. Розріжемо перше наше кільце по проведеній нами лінії. Що отримали? – Два кільця, вужчих за попереднє.
2. А що ми отримаємо, якщо розріжемо лист Мебіуса? Спробуємо? … Що отримали? – Вдвічі довший лист Мебіуса з двома обертами, так звана «афганська петля».
3. Приготуємо інший лист Мебіуса. Проведемо лінію вдвічі ближче до лівого краю. Як ви думаєте, якщо її розрізати, що отримаємо? Перевірте, будь, ласка. – Два листа Мебіуса, одне в одному; менше з одним обертом, більше з двома обертами.
4. Перегорнемо тепер паперову смужку на 360⁰ і розріжемо посередині. Що ж отримаємо? Перевірте. – Дві «афганські петлі», кільце в кільці.
5. Тепер треба продемонструвати ще один відомий в топології фокус – з перетворенням листа Мебіуса. Якщо при склейці смужки в замкнену петлю зробити не один напівоберт кінця на 180 градусів, як зазвичай, а три таких напівоберти, то вийде майже те ж саме, але не зовсім. Нова особливість стане зрозумілою, якщо провести над стрічкою хірургічну операцію «двуділення» – розрізавши її навпіл уздовж осьової лінії. Акуратно розправивши отриманий результат, виявляють, що тепер це трилистий вузол...

Якщо ж розрізати лист Мебіуса з трьома або більшою кількістю напівобертів, то вийдуть кільця, називаються парадромними.

(Слайд 9) Лист Мебіуса – невичерпне джерело для творчості письменників, художників і скульпторів.

1. Відомим художником Эшером був створений ряд літографій з використанням листа Мебіуса. На найбільш відомій його роботі мурашки повзуть по листу Мебіуса.
2. У формі стрічки Мебіуса зроблений популярний атракціон «Американські гірки».
3. Часто використовують цю геометричну фігуру ювеліри при створенні дизайну коштовностей.
4. Існує, наприклад, теорія, що ДНК – це частина листа Мебіуса. Дослідники в області генетики вже навчилися розрізати одно ланцюгову ДНК так, щоб отримати з неї стрічку Мебіуса.
5. Смуга стрічкового конвеєра зроблена у формі листа Мебіуса. Така поверхня дозволяє збільшити термін використання стрічки, так як її зношування буде відбуватися рівномірно.
6. Лист Мебіуса застосовувався в матричних принтерах для продовження терміну придатності фарбувальної стрічки.
7. Стрічка Мебіуса продовжує викликати стійкий інтерес, не тільки у математиків і винахідників, але і у звичайних людей. Вона надихає митців на створення загадкових витворів мистецтва.
8. Її властивості знайшли своє застосування і в побуті.

(Слайд 10) Якщо склеїти разом два листи Мебіуса уздовж країв, то вийде інша дивовижна фігура – пляшка Клейна.

Це мрія середньовічного алхіміка, це містичний досконалий герметичний сосуд, де зовнішнє переходить у внутрішнє і внутрішнє в зовнішнє, який містить сам себе і переходить сам у себе, в якого внутрішнє і зовнішнє пародоксально є одним ...

Як уявити собі, на що схожа вражаюча "пляшка" в реальності?

Виявляється, неможливо побудувати абсолютно правильну модель цього об'єкта в нашому тривимірному світі: тут буде спостерігатися перетин поверхні, що геть відсутнє у чотиривимірному просторі.

Висновок: істинна "пляшка Клейна" може існувати тільки в чотиривимірному вимірі!

А приблизно?

А приблизно це може виглядати так.

Фільм про «пляшку» Клейна. (Слайд 11)