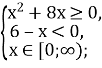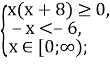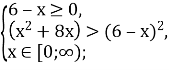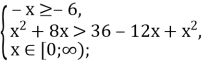Методи розв'язування ірраціональних нерівностей
При розв'язуванні складніших ірраціональних нерівностей, часто використовують метод заміни змінної. В такий спосіб спочатку знаходять область допустимих значень нерівності, тоді виконують заміну змінної. При цьому можна отримати раціональну нерівність або ірраціональну нерівність простішого виду.
1
Метод заміни
При розв’язуванні складніших ірраціональних нерівностей, часто використовують метод заміни змінної. В такий спосіб спочатку знаходять область допустимих значень нерівності, тоді виконують заміну змінної. При цьому можна отримати раціональну нерівність або ірраціональну нерівність простішого виду.
Розв’яжемо нерівність ![]() .
.
Область визначення нерівності:
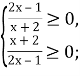
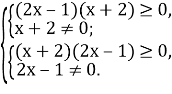
![]()
![]()
![]()
![]() + - +
+ - +
![]()
![]() х
х
2)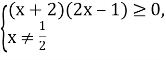
![]()
![]()
![]()
![]() + - +
+ - +
![]()
![]() х
х
Тоді розв’язок системи:
|
|
|
|
х![]() .
.
Зробимо заміну: ![]() ,
, ![]() , t
, t![]()
Отримаємо: t - ![]() ,
, ![]()
![]()
![]()
![]()
![]() D = 49 + 576 = 625,
D = 49 + 576 = 625, ![]() = 25.
= 25.
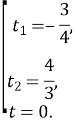
|
- |
t![]() ; 0)
; 0) ![]() .
.
Але t![]()
![]() ;
; ![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
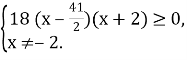
|
- |
![]()
х![]() .
.
Відповідь: х![]() .
.
- Метод множення або ділення
При розв’язуванні нерівностей чи рівнянь інколи використовують спосіб множення або ділення обох частин нерівності чи рівняння на деяку функцію. Це здебільшого приводить до нерівності, нерівносильної даній. Але, при правильному застосуванні цього способу, можна розв’язати деякі нерівності. Для цього користуються твердженням: «Нехай для кожного х з деякої множини D, функція φ(х) визначена і не дорівнює нулю. Тоді на цій множині рівносильні рівняння f(х)=g(х) і f(х)· φ(х) =g(х)· φ(х)». [ 3 ]
Розглянемо нерівність ![]() .
.
Запишемо дану нерівність у вигляді: ![]() .
.
Знайдемо область визначення нерівності: ![]()
![]()
![]()
 Розв’язок першої нерівності:
Розв’язок першої нерівності:
|
- |
х Є (-∞; -8] U [0; ∞).
Розв’язком системи є:
|
|
|
-8 |
х![]()
Помножимо обидві частини нерівності на строго додатну на області визначення функцію у = ![]() . Отримаємо,
. Отримаємо, ![]()
![]() . Нерівність рівносильна сукупності двох систем:
. Нерівність рівносильна сукупності двох систем:
|
- |
х Є (-∞; -8] U [0; ∞).
Розв’язком системи є:
|
|
|
-8 |
х![]()
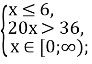
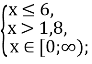
|
|
|
0 1,8 |
х![]()
Отже, розв’язком нерівності є х![]()
Відповідь: х![]()
- Графічний метод
Вивчаючи літературу по даній темі, я наштовхнулася на ще один цікавий спосіб розв’язування ірраціональних нерівностей – графічний.
Він суттєво відрізняється від усі інших, адже замінює аналітичний процес розв’язання на наочно геометричний, тому цей метод є більш практичним. Перевагою його є ще й значне зменшення ймовірності помилок, які виникають під час розв’язування систем, до яких зводяться подані нерівності. Суть графічного методу полягає в тому, що в одній системі координат будуються графіки функцій, записаних в лівій і правій частині нерівності. З малюнка зразу дістаємо наочне уявлення про шукану множину розв’язків.
Приклад. Розв’яжемо нерівність ![]()
Перепишемо нерівність у вигляді ![]()
В одній системі координат побудуємо графіки функцій ![]() і
і ![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
0 |
1 |
2 |
|
|
|
х |
З малюнка одразу ж видно, що відповіддю буде проміжок (1; 2].
Відповідь: ![]()
Аналізуючи ірраціональні нерівності, які зустрічалися на олімпіадах різного рівня з математики, та вказівки до їх розв’язання, я дійшла висновку, що автори їх намагалися розв’язувати нерівності, використовуючи властивості монотонності та обмеженості функції. Хоча інколи це є не досить зрозумілим. На мою думку дані нерівності краще розв’язати графічно. (Див. Додаток А)
- Метод інтервалів
Основною цілю своєї роботи я ставила пошук такого методу, який би дозволяв розв’язувати більшість ірраціональних нерівностей. Для цього я опрацювала значну кількість літератури по цій темі і розв’язала чимало нерівностей. Внаслідок цього дійшла висновку, що будь – яку ірраціональну нерівність можна розв’язати універсальним методом – методом інтервалів.
Доцільність застосування його виникає при необхідності розглянути велику кількість різних варіантів, тобто коли розв’язком нерівності є сукупність великої кількості систем.
Обґрунтуванням методу інтервалів є теорема.
«Теорема. Якщо функція f(х) визначена і неперервна наданому проміжку і не має на ньому нулів, то при всіх значеннях х, що належать даному проміжку, функція f(х) зберігає знак»![]() .
.
Для розв’язування ірраціональних нерівностей f(х)![]()
![]()
- Знаходимо область визначення функції f(х).
- Визначаємо на основі рівносильних перетворень нулі функції, тобто розв’язуємо рівняння f(х)=0.
- Позначаємо нулі функції на області визначення.
- Знаходимо знак функції f(х) на кожному із проміжків, на які розбивається область визначення.
- Записуємо відповідь, враховуючи знак нерівності.
Розглянемо для прикладу нерівність, яка була розв’язана графічно.
Це нерівність ![]()
Запишемо її у вигляді f(х)![]()
![]()
Область визначення функції f(х) =![]() визначимо із системи:
визначимо із системи:
![]()
![]()
![]()
Нулі функції знаходимо із рівняння: ![]()
![]() ,
, ![]()
![]()
![]()
![]() ,
, ![]() За теоремою Вієта х1 = -2, х2 = 1.
За теоремою Вієта х1 = -2, х2 = 1.
Позначимо нулі функції на області визначення, знайдемо знак
f(х) =![]() на кожному проміжку.
на кожному проміжку.
|
-3 - |
Відповідь: ![]()
Розглянемо другий приклад: ![]()
Маємо функцію f(х) =![]() ,область визначення якої є множина значень нерівності
,область визначення якої є множина значень нерівності ![]() , тобто
, тобто ![]()
Знаходимо нулі функції. Для цього розв’яжемо рівняння: ![]()
![]()
![]()
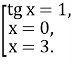
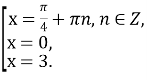
Розбиваємо область визначення f(х) точкою ![]() на проміжки і знаходимо знак функції на кожному із них:
на проміжки і знаходимо знак функції на кожному із них:
|
0 |
Відповідь: ![]() .
.
Таких прикладів можна навести безліч. Але на мою думку, всі вони підтверджують універсальність методу інтервалів. Це проявляється в тому, що розв’язання ірраціональних нерівностей набагато спрощується. Адже воно зводиться до розв’язування ірраціональних рівнянь, а не систем нерівностей.

про публікацію авторської розробки
Додати розробку