Методична розробка "Форми контролю знань учнів на уроках математики шляхом впровадження інтерактивних методів""
Методична розробка
по темі
«Форми контролю знань учнів
на уроках математики
шляхом впровадження інтерактивних технологій»
викладача математики
Шмакової О.Л.
Зміст
Вступ . …………………………………………………………....3
Розділ І Сутність контролю знань учнів
1.1 Принципи контролю знань учнів ……………………………………5
1.2 Функції контролю знань ……………………………………………..7
1.3 Форми контролю навченості учнів ………………………………….7
Розділ ІІ Приклади контролю знань учнів шляхом впровадження інтерактивних технологій …………………………………………….17
Висновки ………………………………………………………………..34
Список використаних джерел ………………………………………..35
Вступ
У зв’язку з переорієнтацією процесу навчання з інформативної форми на розвиток особистості учня та впровадження особистісного підходу постала необхідність змінювати технологічний підхід до навчання. Тому необхідно шукати і використовувати нові технології для успішного навчання учнів.
У наш час існує понад 200 інноваційних технологій, які передбачають використання сукупності наукових прийомів, методів, які дозволяють вчителю застосовувати свої знання та вміння для організації цілеспрямованої, творчої, захоплюючої роботи учнів.
Найпоширенішими технологіями, які вже ефективно використовуються творчими викладачами є інтерактивні технології.
Понад 2400 років тому Конфуцій сказав:
Те, що я чую, я забуваю.
Те, що я бачу, я пам’ятаю.
Те, що я роблю, я розумію.
Ці три прості твердження обґрунтовують необхідність використання активних методів навчання. Дещо змінивши слова великого китайського педагога, можна сформулювати кредо інтерактивного навчання:
Те що я чую, я забуваю.
Те, що я бачу й чую, я трохи пам’ятаю.
Те, що я чую, бачу й обговорюю, я починаю розуміти.
Коли я чую, бачу, обговорюю й роблю, я набуваю знань і навичок.
Коли я передаю знання іншим, я стаю майстром.
Інтерактивні технології можна представити як різновид активних методів навчання. Як правило, сучасна система вимагає від вчителя охоплення великого обсягу інформації, вона орієнтована на рівні «знання» й «розуміння». Це підштовхує вчителя на використання в основному пасивних методів навчання, які не дають можливості учням оволодіти навичками думати, розуміти суть речей, осмислювати ідеї та концепції і вже на основі цього вміти шукати потрібну інформацію, трактувати її та застосовувати в конкретних умовах, формувати й відстоювати особисту думку, чому сприяють інтерактивні технології.
Але яку б технологію на уроці ми не використовували, обов’язково треба перевіряти, іншими словами, контролювати, процес засвоєння знань учнів.
Контроль знань учнів – важлива ланка в складному процесі навчання. Він включає не тільки одержання і фіксування підсумкової інформації про результати навчання, а й сприяє виявленню нерозв’язних завдань навчання та причин невстигання учнів, самоаналізу вчителем та учнем своєї діяльності, обговоренню підсумків спільної діяльності і, найголовніше, визначенню вчителем вихідних даних (на основі набутих учнями вмінь і навичок) для здійснення нового циклу процесу навчання, більш високого за рівнем, досконалішого порівняно з попереднім.
Без чіткої системи виявлення результатів навчальної діяльності учнів не можна ефективно керувати їхнім навчанням, своєчасно запобігати неуспішності, коригувати відхилення в засвоєнні програмового матеріалу, організовувати диференційовану індивідуальну роботу з учнями.
Перевірка й оцінювання результатів навчання сприяє формуванню в учнів оціночного ставлення до себе і своєї діяльності, виробляє почуття самокритичності, принциповості, а також таких рис характеру, як витривалість, наполегливість, уміння володіти собою. Необхідно створювати певні дидактичні умови для активного формування в учнів адекватної самооцінки, яка вважається серцевиною особистості, регулятором її поведінки і діяльності.
Розділ І Сутність контролю знань
1.1 Принципи контролю навчальних досягнень учнів
Відомі чотири принципи контролю, згідно яких доцільно планувати його форми і засоби для успішної реалізації основної методичної мети вивчення курсу.
1. Визначення мети контролю знань учнів
Формування мети контролю повинно бути орієнтоване на той зміст навчального курсу або ті чи інші його аспекти, засвоєння яких буде контролюватись, причому про необхідні результати навчання і бажані їх показники учні повинні бути проінформовані, наприклад, у вигляді інформаційної розробки.
2.Вставновлення конкретних об’єктивно необхідних результатів контролю знань
Загальна мета контролю повинна конкретизуватись через вимоги. Виражені через дії вимоги стають тими необхідними (бажаними) результатами засвоєння, з якими при здійсненні контролю учитель повинен співвідносити результати досягнень учнів. При цьому в плануванні вимог контролю засвоєння результатів навчального матеріалу доцільно передбачити по можливості не лише виявлення результатів, а й їх діагностику, тобто встановлення причин помилок в знаннях учнів (особлива увага повинна приділятись самодіагностиці на основі самооцінці виконаної роботи).
Таким чином, під показником засвоєння слід розуміти бажані дії учнів, що свідчать про досягнення того чи іншого елемента результату засвоєння. Разом з цим необхідні результати засвоєння (підсумкові знання) можна визначити і як спільний показник мети навчання, і як сукупність показників засвоєння і зв’язків між ним, встановлених в залежності від конкретного навчального матеріалу і мети навчання (засвоєння основ науки).
3. Організація контролю знань учнів
При визначення необхідних результатів засвоєння треба брати до уваги місце контролю при вивченні матеріалу. В залежності від місця контролю виділяють такі його види: поточний (контроль засвоєння навчального матеріалу під час пізнавального процесу), підсумковий по темі (тематичний) або другої логічно завершальної частини навчального матеріалу (поетапний підсумковий контроль) і підсумковий по курсу навчання. Крім того, визначення остаточного змісту для конкретного контролю пов’язане з його формою – масовою або індивідуальною, а також із способом контролю – письмовий, усний, усно письмовий, практичний.
Після того, як будуть визначені всі вказані організаційні аспекти і встановлені необхідні результати засвоєння для конкретного контролю, можна приступати до підбору і конструювання відповідних його засобів – контрольних і самостійних робіт, заліків, тестів.
4. Знаходження шляхів об’єктивного аналізу і оцінки результатів контролю
Аналіз і оцінка підсумків контролю передбачають співставлення якості досягнутих учнями результатів із запланованими необхідними результатами засвоєння. По елементний аналіз відповідей (усних чи письмових) учнів сприяє підвищенню якості не лише якісної, а, іноді, і кількісної оцінки.
Такий аналіз полягає в розбитті контрольного завдання на можливі елементарні складові частини у відповідності з показниками засвоєння, що вичавлюються, і аналізування відповідей учнів на основі цих показників та зв’язків між ними.
Додержуючись основних принципів вибору мети, об’єктивності оцінки результатів контролю, вчитель-предметник має великі можливості у досягненні бажаних результатів навчання, як наслідок, формуванні розумової культури учнів.
1.2 Функції контролю знань
Для того, щоб педагогічно німотно визначити мету вивчення нового матеріалу, необхідно точно знати, що вже досягнуто унаслідок навчання.
Контроль досягнутих результатів має низку функцій. Розглянемо деякі з них.
Перша функція контрою може бути визначена як навчаюча. Контроль сприяє поглибленню, розширенню, удосконаленню знань учнів. Нормальний розвиток навчального процесу передбачає зворотний зв’язок у двох його різновидах: «учень-вчитель» і «учень-учень». Ідеться про так званий зовнішній і внутрішній зв’язок у навчанні.
Друга функція контролю – виявлення знань, умінь і навичок, а також існуючих ще в них прогалин – діагностична.
Третя функція контролю – вимірювання і оцінка знань і навичок учнів.
Четверта функція контролю – виховна або функція стимулювання (виховання волі, характеру, дисципліни, навичок систематичної самостійної праці та ін.).
П’ята функція контролю – розвиваюча. Контроль знань сприяє розвитку психічних процесів особистості – уваги, пам’яті, мислення, інтересів, пізнавальної активності, мовлення учнів.
Шоста функція контролю – прогностична (методична). Передусім вона стосується вчителя, який отримує досить точні дані для оцінки своєї праці, результатів запровадження своєї методики викладання, шляхів подальшого вдосконалення навчання. Однак така функція контролю стосується і учнів. Контроль допомагає їм прогнозувати свою навчальну роботу.
1.3 Форми контролю навченості учнів.
Форми контролю передбачають:
• відкритість, конкретність та обґрунтованість вимог на кожному етапі засвоєння знань, умінь та навичок;
• різнорівневий підхід до оцінювання результатів навчальної праці;
• оцінювання кінцевого результату засвоєння з урахуванням позитивних проміжних результатів;
• самоаналіз і самооцінку навчально-пізнавальної діяльності учнів;
• самостійність учнів у виборі темпів засвоєння та рівня кінцевого результату.
1. Деякі форми перевірки домашнього завдання:
Контроль за засвоєнням навчального матеріалу починається з перевірки домашнього завдання, яку можна проводити різними способами. Розглянемо деякі з них.
Самоперевірка за зразком
Цей спосіб доцільно застосовувати на уроці, наступному після уроку пояснення нового матеріалу. Зразок розв’язання домашнього завдання записано на дошці чи спроектовано на екран через кодоскоп, мультимедійний проектор. Коли розглядається розв’язання-зразок, який усно коментують учні, зошити у них закрити. Після цього учні відкривають зошити і кожний перевіряє свою роботу за зразком, підкреслює помилки та виставляє оцінку простим олівцем. Учитель збирає зошити, виставляє оцінки – за якість самоперевірки і за роботу над помилками червоним кольором.
Взаємоперевірка за допомогою зразка
На наступних уроках учні перевіряють за зразком уже не власну домашню роботу, а свого сусіда і виконують роботу над помилками. Як в першому випадку, кінцеву перевірку здійснює вчитель. Іноді збираються зошити і відразу роздаються, але так, щоб кожний учень одержав не свою, а чужу роботу, і уже не сусіда. Учні можуть побачити, як виконують домашнє завдання однокласники, порівняти свої роботи з роботами інших учнів.
Перевірка консультантами
Для перевірки домашнього завдання залучаються кращі учні, зошити яких перевіряються завчасно, оскільки вони надалі служать зразком. Іноді з класу вибирається контрольна група з трьох учнів. Кожен ряд знає, кого він може висунути кандидатом у консультанти. Група контролю сідає окремо, перевіряє та оцінює роботу. На перевірених роботах учні-консультанти ставлять свій підпис, потім роздають зошити з короткими усними роз’ясненнями щодо допущених помилок. Якщо виникають непорозуміння, то вчитель виступає як арбітр і показує правильний зразок або дає власне роз’яснення.
Письмова діагностична робота
Цей вид роботи використовується, щоб з’ясувати чи виконали учні домашнє завдання самостійно. До роботи включаються завдання, аналогічні до тих, які виконувалися вдома. Робота дається в кількох варіантах або для окремої групи учнів, або індивідуально для кожного учня залежно від дидактичного матеріалу. Якщо в класі є можливість розміщення крім основної ще й бічних класних дошок, за якими одночасно може працювати кілька учнів, то при такому контролі учні публічно захищають самостійність виконання домашнього завдання. Одну із задач ще раз доцільно обговорити з класом.
Перевірка-консультація
Коли задавалося диференційоване домашнє завдання різних ступенів складності, то пропонується учням викласти те, що вони зрозуміли у вигляді запитань. Відповідають на запитання ті учні, які повністю виконали домашню роботу. Вчитель підбиває підсумки
2. Інші форми контролю
Опитування парами
Таке опитування доцільне, якщо урок не перевантажений новим матеріалом або є уроком узагальнення й систематизації знань після вивчення певного матеріалу. Суть опитування – один учень із пари оголошується «вчителем», а другий – «учнем». Учитель ставить запитання класу. «Учні» повертаються обличчям до «вчителів» і напівголосно відповідають. Через певний проміжок часу вчитель оголошує правильну відповідь. Набір запитань і відповідей оцінюють «вчителі» системою знаків «+» або «–». Набір таких знаків перетворюється в підсумкову оцінку.
Самостійна робота
Цю традиційну форму контролю знань застосовують після вивчення окремого матеріалу і набуття певних навичок. Видами таких робіт є:
• напівсамостійні роботи – план розв’язування задачі знаходиться колективно під керівництвом вчителя, а саме розв’язання здійснюється учнями самостійно;
• пошукові роботи з вказівками – для розв’язання пізнавальних задач, що містять нові знання; учні пробують розв’язати задачу самостійно, звертаються до вчителя за допомогою і одержують її у вигляді підказок, вказівок або рекомендацій;
• спостереження – вчитель вказує учням мету, що і для чого спостерігати, дає певний план спостереження і збору інформації, пояснює, яку роботу потрібно виконати; учень веде спостереження за об’єктами – математичні тексти, малюнки, моделі тощо;
• складання задач – пропонується після засвоєння математичного поняття чи його властивостей, після закріплення вивченого теоретичного матеріалу; в кінці вивчення значної теми оголошується конкурс на створення або відшукання оригінальних задач з цієї теми;
• творчі роботи – вчитель дає тему роботи або завдання; учень складає план і виконує роботу. Завданням на творчу роботу можуть бути:
1) розв’язання задач підвищеної складності;
2) підбір і розв’язання цікавих задач по темі;
3) новий спосіб доведення теореми і розв’язання задачі;
4) реферування математичної статті;
5) створення серії малюнків геометричних фігур із розглядом всіх їхніх властивостей;
6) створення опорного конспекту значної теми;
7) виготовлення наочності, зокрема, комплекту моделей геометричних тіл;
8) тривале спостереження на задану тему, їх опис, виконання замірів і розрахунків;
9) підготовка та участь в математичних шкільній олімпіаді.
Теоретична розминка
Кілька учнів працює біля дошки, решта може ставити їм запитання з усього теоретичного матеріалу, який повторюється. Учні відповідають почергово за бажанням. Вчитель доповнює запитання учнів наперед підготовленими власними запитаннями. Така розминка звичайно використовується наприкінці вивчення теми.
Математичний диктант
Це короткочасна перевірочна робота, яку учні сприймають на слух (повністю або частково) і виконують письмово чи записують лише результати. Така мобільна форма контролю дає можливість своєчасно усувати прогалини в знаннях учнів, формувати навички самоконтролю. Її можна ефективно використовувати в усіх класах.
Тестування
Тести дають змогу оперативно контролювати навченість учнів, не потребують значних витрат часу і дають об’єктивні дані. Оптимальна кількість запропонованих відповідей – чотири. Учні позитивно сприймають таку форму контролю. Тести поділяються на:
• альтернативні – вибір однієї правильної відповіді з двох запропонованих: «так» або «ні», «правильно» або «неправильно»;
• відповідностей – запис або позначення стрілками певних відношень, залежностей;
• виправлення помилок – виключення зайвого слова або неправильного позначення чи запису;
• вибіркових – вибір однієї правильної відповіді з 3-5 запропонованих у поставленому завданні.
Проте тести мають свої недоліки, оскільки вчителю не відомий хід міркувань учня, що приводить до відповіді. Не виключений випадок, коли учень може навмання правильно поставити стрілку, виключити зайве слово чи вибрати відповідь.
Залік
Запитання з теоретичної частини матеріалу роздаються учням на початку її вивчення. Це дає можливість кожному учню добре підготуватися до заліку. Залікова оцінка враховується вчителем під час виставлення підсумкової оцінки. Урок-залік відбувається нетрадиційно – або у формі математичного рингу, або у формі математичної естафети, або естафети взаємоопитування між учнями (один учень відповідає іншому – тому, який вже відповів).
Спринт-робота
Часто вчителю потрібна інформація про те, яка частина учнів засвоїла алгоритм виконання певного завдання. Для цього пропонується короткочасна перевірочна робота на швидкість виконання завдання. Перші 8-10 учнів, які виконали роботу, кладуть зошити на стіл вчителя. Учитель разом з контрольною групою виконує експрес-перевірку. Позитивні бали виставляються тим, хто впорався із завданням. Це дає змогу постійно визначати можливості учнів для проведення диференційованої роботи, а також лідерів груп для проведення групових форм занять або практикуму.
Експрес-опитування
Це можуть бути стислі усні або письмові відповіді (наприклад, за картками на знання основних понять), завдання типу «продовжити речення», заповнити таблицю, намалювати діаграму, скласти схему тощо.
Розширене опитування
Вчитель пропонує учням усно або письмово дати відповідь на поставлене запитання з поясненнями окремих положень, з наведенням аргументів, прикладів. Під час відповіді вчитель та інші учні можуть ставити додаткові запитання; варіантами контролю є усний «екзамен» з білетом, письмова контрольна робота, домашнє есе.
Самооцінка
Оцінка самими учнями своєї роботи (своєї особисто або інших колег), а також заняття в цілому є цінною формою контролю.
Для самооцінки учнями своєї роботи може застосовуватися метод питань-відповідей; можна попросити учнів поставити однокласникам оцінки і мотивувати їх (наприклад, у випадку перевірки упорядкування документів один одного учні можуть поставити оцінку залежно від повноти використання практичних порад).
Домашня контрольна робота
Виконуючи такі роботи, учень самостійно працює над теоретичним матеріалом, знаходить свої способи та прийоми розв’язування деяких задач.
Методика проведення домашніх контрольних робіт зводиться до наступного: на початку вивчення нової теми кожен учень одержує завдання, яке він повинен розв’язати протягом вивчення теми. Серед завдань є такі, які потребують додаткового вивчення теоретичного матеріалу. Під час виконання роботи учень має можливість одержувати консультації як від своїх однокласників, так і від вчителя.
Зміст роботи відповідає вимогам зовнішнього оцінювання, а тому складається з трьох частин:
• завдання обов’язкового рівня;
• завдання підвищеного рівня;
• завдання поглибленого рівня.
Найчастіше робота пропонується в чотирьох варіантах.
Завдання повинні бути виконані до кінця вивчення теми. Захист роботи проводиться під час написання самостійної перед заліковою контрольною роботою. Самостійна робота пропонується такого ж змісту, що й домашня контрольна робота, але зі зміною варіантів для кожного учня. Результати написання такої самостійної роботи свідчать про рівень роботи кожного учня протягом теми, дають можливість учителю побачити слабкі місця у вивченні теми, які відпрацьовуються потім перед написання контрольної роботи.
Обов’язковою умовою змісту такої роботи є включення всіх основних видів завдань. Це дає змогу учневі вивчити тему в повному обсязі.
Контрольна робота
Це завершальний етап контролю знань учнів з теми. Перед контрольною роботою повідомляється кількість балів за кожну задачу або завдання, а на уроці-аналізі розв’язуються ті завдання, які викликали найбільші ускладнення під час виконання контрольної роботи. Зошити роздаються так, щоб кожен учень спочатку одержав не свій зошит. Пропонується визначити характер помилок і аргументувати виставлену оцінку.
Домашнє завдання після аналізу контрольної роботи: придумати і розв’язати задачу, аналогічну до тієї, в якій кожний учень допустив помилку.
Розділ ІІ Приклади контролю знань учнів
шляхом впровадження інтерактивних технологій
Тема: Розв’язування показникових рівнянь
Хід уроку
ІІІ Сприйняття і засвоєння нового матеріалу
Пропонується застосування інтерактивної технології «Ажурна пилка».
На попередньому уроці вчитель роздав кожному учневі картку певного кольору з номером на ній (від 1 до 5). Сформулювалось 5 груп по 5 осіб.
|
«червоні» - сформулювати означення показникового рівняння, пояснити на прикладах, коли рівняння має корінь і коли коренів немає |
|
«зелені» - сформулювати властивість |
|
«сині» - сформулювати властивість |
|
«фіолетові» - розв’язати рівняння а) |
|
«жовті» - перевірити, які з чисел є коренем рівняння |
На уроці учні об’єднуються відповідно до кольору картки – в «домашні групи», а потім в «експертні» групи.
1. Робота «домашніх груп» - учні обмінюються інформацією проводять взаємоопитування, розв’язують завдання, підготовлені вдома.
2. Робота «експертних груп» – учні обмінюються інформацією, яку одержали в «домашній групі» (роблять запис у зошитах).
3. Учні знову об’єднуються в «домашні групи» і обмінюються здобутою інформацією.
Оцінювання
• кожна «домашня група» отримує перелік запитань:
1. сформулювати означення показникового рівняння, пояснити на прикладах, коли рівняння має корінь і коли коренів немає
2. сформулювати властивість ![]() , довести її та пояснити на прикладах
, довести її та пояснити на прикладах
3. сформулювати властивість ![]() , довести її та пояснити на прикладах
, довести її та пояснити на прикладах
4. розв’язати рівняння а) 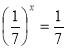 , б)
, б) ![]() і пояснити спосіб розв’язування
і пояснити спосіб розв’язування
5. перевірити, які з чисел є коренем рівняння ![]() і пояснити алгоритм виконання задачі
і пояснити алгоритм виконання задачі
За кожну правильну відповідь – 1 бал.
ІV Закріплення вивченого матеріалу
А) Робота в «домашніх» групах
Кожній «домашній групі» пропонується розв’язати показникові рівняння (завдання кожного рівня з’являється на дошці за допомогою мультимедійного проектора)
Рівень А:
1) 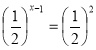 ; 2)
; 2) 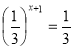 ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
(Відповіді: 1) 3; 2) 0; 3) 2; 4) 5)
Рівень Б:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
(Відповіді: 1)5; 2) 3; 3) -2; 4) 0)
Рівень В:
1) ![]() ; 2)
; 2) 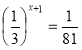 ; 3)
; 3) ![]() ; 4)
; 4) ![]()
(Відповіді: 1) 3; 2) 3; 3) 2; 4) -1).
Оцінювання
• за приклади рівня А – 0,5 бали,
• за приклади рівня Б – 1 бал,
• за приклади рівня В – 1,5 бали.
Б) Колективне розв’язування задач в групах:
|
1) Відповідь: 3 |
2) Відповідь: -4; 3 |
3) Відповідь: 4 |
|
4) Відповідь: -3; 1 |
5) Відповідь: -1; 1 |
Робота з підручником № 1 (6, 8, 9) |
Оцінювання:
• правильно розв’язане завдання – 2 бали.
Тема: Призма
Хід уроку
ІІІ Закріплення вивченого матеріалу
Пропонується застосування інтерактивної технології «Робота в малих групах».
Для цього заздалегідь готуються картки із завданнями (слайди), учні класу за рівнем підготовленості об’єднуються в групи по 3-4 учні.
Оцінювання
• якщо учень розв’язує обидві задачі середнього рівня, він отримує 4 балів,
• за правильне розв’язування задач достатнього рівня – 6 балів,
• задачі високого рівня оцінюються 9 балами.
|
Картка 1 (середній рівень підготовки) |
|
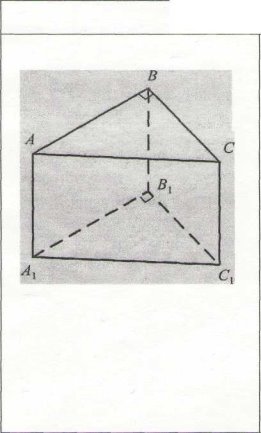
Задача 1. Основою прямої трикутної призми є прямокутний трикутник з катетами 3см і 4 см. Висота призми 5 см. Знайти площу повної поверхні призми.
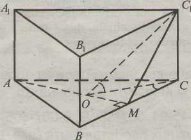
Задача 2. АВСА1В1С1 – правильна трикутна призма. О – центр трикутника АВС. ОМ
|
|
Картка 2 (достатній рівень підготовки) |
|
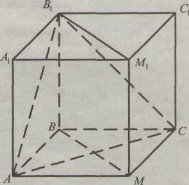
Задача 1. Дано правильну шестикутну призму зі стороною основи 8 см і висотою 2,5 см. Знайти площу бічної поверхні призми. Задача 2. АВСА1В1С1 – трикутна призма. О – центр трикутника А1В1С1. АВ=АС=ВС. АО – висота призми. Знайти величину кута ВВ1С1.
|
|
Картка 3 (високий рівень підготовки) |
|
Задача 1. В основі прямої призми лежить ромб. Бічна діагональ призми дорівнює d і нахилена до площини основи під кутом Задача 2. Дано правильну чотирикутну призму. Знайти відношення площ АВ1С та ВВ1М1М.
|
У разі ускладнень, які можуть виникнути під час розв'язування, за допомогою можна звернутися до слайдів (наприклад, слайд 1), на яких є не лише детальне розв'язання, а й виконано малюнки та вказані всі вимоги до оформлення завдань перших задач карток.
Слайд 1
|
Розв’язання задачі 1 картки 1 |
|
|
|
Нехай АВСА1В1С1 - дана пряма трикутна призма: АВ=4см, ВС= 3см, АА1=5см, SП=Sб+2S0 Sб=Н∙Р, де Н - висота, Р - периметр основи. Р=АВ+ВС+АС Знайдемо АС з ΔАВС:
АС2=АВ2+ВС2, АС= Р=3+4+5=12 (см)
Sб=12∙5=60 (см2), So= SП=60+2∙6=72 (см2) Відповідь: 72 см2 |
Щодо розв'язування другого завдання, то на картці, крім умови, є малюнки, які допоможуть учням.
Учні тієї групи, яка у своєму рівні правильно виконала завдання, розподіляються серед інших груп свого рівня. Коли учні якогось рівня повністю розв'язали завдання, вони переходять на вищий рівень, а учні високого рівня допомагають учням нижчого.
У разі, коли всі групи рівня не можуть виконати завдання, його колективно обговорюють і розв'язання записують на дошці. Обґрунтування
розв'язування доцільно провести у вигляді «Мозкового штурму», що спонукає до мислення, дає можливість вислухати різні ідеї, а також скорочує час розв'язування проблеми.
Після виконання завдань відбувається обговорення результатів.
Один із представників групи кожного рівня (обирається колективно рівнем) повідомляє основні етапи розв'язування задачі 2 та оголошує висновок рівня про «корисність» задачі. Наприклад, «корисність» задачі 2 середнього рівня — це повторення властивостей центра трикутника, рівнобедреного трикутника та співвідношень у прямокутному трикутнику.
Оцінювання
• представник групи, який відповідає біля дошки отримує додатково 1 бал
Отже, залежно від рівня підготовленості, учень може розглянути від двох до шести задач різного рівня складності.
IV Практичне закріплення матеріалу
Колективне поетапне розв'язування та оформлення задачі в зошиті, що має на меті не лише спонукання розумової діяльності учнівського колективу, а й виховання вміння стисло висловлювати свої думки та правильно оформляти розв'язання задачі.
Задача. Основа прямої трикутної призми – рівнобедрений трикутник з кутом ![]() при вершині. Діагональ бічної грані, якій належить бічна сторона цього трикутника, дорівнює k і утворює з площиною основи кут
при вершині. Діагональ бічної грані, якій належить бічна сторона цього трикутника, дорівнює k і утворює з площиною основи кут ![]() . Визначити площу повної поверхні призми.
. Визначити площу повної поверхні призми.
Оцінювання
• за правильне розв’язування задачі – 7 балів
Тема: Розв’язування задач на використання комбінацій (без повторень), перестановок (без повторень), розміщень (без повторень)
Хід уроку
ІІ Перевірка домашнього завдання
Для перевірки домашнього завдання пропонується обмінятися зошитом з сусідом за партою. Розв’язання завдань з’являється на дошці за допомогою мультимедійного проектора.
Такий вид роботи дає можливість учням не тільки навчитися перевіряти завдання за готовими розв’язками, а й ознайомити з розв’язком задачі свого одногрупника.
|
Розв’язання домашніх вправ |
|
Вправа № 113
Оскільки з аксіомою І через дві точки можна провести лише одну пряму, то число п усіх прямих дорівнює числу комбінацій із 10 по 2, тобто п= Відповідь: 45
Вправа № 116
Оскільки обидві жінки увійдуть до списку, число всіх випадків дорівнює кількості вибору з 30-2=28 (співробітників) двох чоловіків: Відповідь: 378
Розв’язання рівняння :
Оскільки 7!
8-х=х, х=4. Перевірка.
Відповідь: 4 |
Оцінювання
• за правильно виконані завдання (№ 113, № 116) – по 2 бали,
• за правильно розв’язане рівняння – 4 бали.
Тема: Пряма (правильна) призма.
Площі бічної та повної поверхонь призм
Хід уроку
ІІ Перевірка домашнього завдання
Для перевірки теоретичної частини пропонується гра «Хрестики-нолики». Група діляться на 2 команди:
1 – «хрестики»,
2 – «нолики».
Вчитель читає запитання, яке з’являється на дошці за допомогою мультимедійного проектора. Команда, яка першою правильно відповідає на запитання, ставить на решітці «свій знак». Якщо відповідь невірна або неповна, право на відповідь має команда-суперниця.
|
|
|
|
|
|
|
|
|
|
|
|
Оцінювання
• кожна правильна відповідь оцінюється 1 балом
Тема: Контрольна робота по темі
«Вступ до стереометрії»
Хід уроку
ІІ Виконання контрольної роботи
Однією з найпоширеніших форм контролю знань учнів є контрольна робота.
Пропонується контрольна робота у вигляді тестових завдань 4 рівнів складності. Всі завдання одночасно з’являються на дошці за допомогою мультимедійного проектора.
І рівень. У завдання 1-3 виберіть і підкресліть правильну відповідь.
1. Через три точки, що не лежать на одній прямій:
а) можна провести тільки одну площину
б) не можна провести жодної площини
в) можна провести безліч площин
2. Через пряму і точку, що лежить на ній:
а) можна провести тільки одну площину,
б) не можна провести жодної площини,
в) можна провести безліч площин.
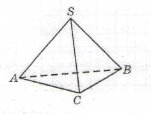
3. На малюнку зображено тетраедр SABC. Прямі АВ і SC:
|
|
а) перетинаються, б) паралельні, в) мимобіжні
|
ІІ рівень.
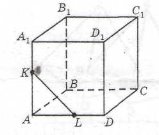
4. Користуючись малюнком із зображенням куба АВСDA1B1C1D1 визначте взаємне розміщення прямих, наведених у таблиці.
|
|
|
Прямі |
АD |
BB1 |
|
KL |
|
|
||
|
DD1 |
|
|
5. Визначте істинність тверджень, які наведено нижче. (Якщо твердження істинне, поставте знак «+», якщо хибне «-»).
□ Якщо три вершини ромба лежать у деякій площині, то й четверта його вершина лежить у цій площині.
□ Якщо дві точки кола належать деякій площині, то й усе коло лежить у цій площині.
□ Через чотири точки, що лежать на одній прямій, можна провести площину.
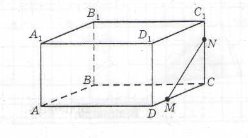
6. Використовуючи малюнок із зображенням прямокутного паралелепіпеда АВСDA1B1C1D1 знайдіть (побудуйте) точку перетину прямої МN з площиною А1В1С1
|
|
ІІІ рівень.
7. Прямі а і b перетинаються, пряма с перетинає пряму а і паралельна прямій b. доведіть, що прямі а, b, с лежать в одній площині.
IV рівень. Розв’яжіть одну з наведених задач.
8. Точки А, В, С, D не лежать в одній площині, точки K, L, M, N – середини відрізків АD, DC, BC, AB відповідно. Знайдіть градусну міру кута KLM, якщо AC=BD, KL=LN.
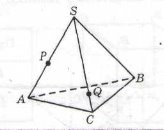
9. Використовуючи малюнок із зображенням піраміди SABC, побудуйте пряму перетину площин PQB і ABC та запишіть послідовність виконання дій.
|
|
Оцінювання
• за І рівень – 1,5 бали,
• за ІІ рівень – 2,5 бали,
• задачі ІІІ рівня – 6 балів,
• задачі IV рівня – 9 балів.
Тема: Розв’язування задач на застосування інтеграла. Самостійна робота
Хід уроку
ІІІ Закріплення набутих знань
Перевірку теоретичних знань учнів пропонується провести у вигляді інтерактивної вправи «Незакінчені речення».
- Обернена операція до диференціювання називається …
- Наведіть приклади задач, які приводять до поняття визначеного інтеграла
-
В формулі
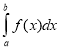 :
: 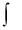 - знак визначеного …; а, b – межі…; y=f(x) - … функція; f(x)dx - … вираз; x – змінна …
- знак визначеного …; а, b – межі…; y=f(x) - … функція; f(x)dx - … вираз; x – змінна …
- Записати формулу Ньютона –Лейбніца
- Застосування визначеного інтеграла: а) для обчислення площ …; б) обчислення об’ємів…
- Визначений інтеграл у фізиці застосовують для обчислення …
Оцінювання
• за кожну правильну відповідь – 0,5 бали. Ці бали за бажанням додаються до оцінки за виконання самостійної роботи
ІV Виконання самостійної роботи
Самостійна робота складається з трьох частин. Розв’язки оформлюються в зошиті, а результатами записуються у бланк відповідей. На перевірку здається і зошит, і бланк відповідей.
|
Бланк відповідей Частина 1
Частина 2
Частина 3
|
Частина 1
Завдання 1-6 мають по 5 варіантів відповідей, з яких лише одна правильна. Оберіть правильну відповідь, та позначте її в бланку відповідей.
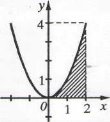
1. Якими лініями обмежена фігура, зображена на малюнку?
|
|
|
А |
Б |
В |
Г |
Д |
|
f(x)=x2, х=2, у=4 |
f(x)=x2, х=2, х=0 |
f(x)=x3, х=2, у=0 |
f(x)=x3, у=2, у=0 |
f(x)=x2, х=2, у=0 |
2. Для функції f(x)=2х знайдіть первісну, графік якої проходить через точку А(2;5)
|
А |
Б |
В |
Г |
Д |
|
F(х)=х2+2 |
F(х)= |
F(х)=х2+1 |
F(х)=х2+23 |
F(х)=х2-2 |
3. Знайдіть площу фігури, обмеженої лініями f(х)=х2+1, у=0, х=0, х=2.
|
А |
Б |
В |
Г |
Д |
|
|
12 |
10 |
|
|
4. Обчисліть інтеграл ![]()
|
А |
Б |
В |
Г |
Д |
|
4 |
|
|
|
2,6 |
5. Вкажіть, яка з функцій є розв’язком диференціального рівняння у/=4у
|
А |
Б |
В |
Г |
Д |
|
у=е4х |
у=2е4х |
у=2е2х |
у=2ех |
у=2ех+С |
6. Знайдіть найбільший розв’язок нерівності (х+3)2 ![]() х2+4х+12
х2+4х+12
|
А |
Б |
В |
Г |
Д |
|
1,5 |
3 |
-1,5 |
3 |
1 |
Частина 2
У завдання 7-8 наведіть розв’язання і відповіді у вигляді десяткових дробів, впишіть у бланк відповідей.
7. Знайдіть значення постійної С для функції F(х), графік якої проходить через точку М(-1;2), якщо F/(х)=х4.
8. Знайдіть площу фігури, обмеженої лініями у=х2-4, у=х2=1, х=-2, х=2 з точністю до 0,1.
Частина 3
Розв’язання завдання 9 має містити повне пояснення.
9. Швидкість руху тіла задано функцією v=(2t2+t). Який шлях пройде тіло за 6 с від початку руху?
Оцінювання
• частина перша – 6 балів,
• частина друга – 3 бали,
• частина третя – 3 бали.
Тема: Розв’язування задач на обчислення елементів тіл обертання
Хід уроку
ІІІ Закріплення набутих знань
Група поділяється на дві частини: 1 варіант і 2 варіант.
Робота виконується в три етапи.
І етап: Обидва варіанти спочатку розв’язують задачі рівня А. Розв’язування проводиться у вигляді напівсамостійної роботи – план розв’язування знаходиться колективно під керівництвом вчителя, а саме розв’язання здійснюється учнями самостійно.
ІІ етап: Обидва варіанти розв’язують задачі рівня Б. Вчитель допомагає лише тим учням, в яких виникли складності.
ІІІ етап: Учні об’єднуються в «малі групи» для розв’язання задач рівня В. «Група» складає план і виконує роботу.
|
Варіант А 1 |
Варіант А 2 |
|
1. Прямокутник з периметром 16см і площею 15 см2 обертається навколо більшої сторони. Знайдіть площу поверхні тіла обертання.
2. Рівнобедрений трикутник з бічною стороною b і кутом при основі 3. Прямокутна трапеція з основами 2 і 5 см і меншою бічною стороною 4см обертається навколо більшої основи. Знайдіть повну поверхню тіла обертання. |
1. Прямокутник з діагоналлю 10см, сторони якого відносяться як 3:4, обертається навколо меншої сторони. Знайдіть площу поверхні тіла обертання.
2. Рівнобедрений трикутник з основою а і кутом при вершині 3. Рівнобічна трапеція з основами 4 і 10см і висотою 4см обертається навколо більшої основи. Знайдіть повну поверхню тіла обертання. |
|
Варіант Б 1 |
Варіант Б 2 |
|
1. Прямокутний трикутник з гіпотенузою с і гострим кутом а обертається навколо гіпотенузи. Знайдіть площу поверхні і об’єм тіла обертання. 2. Трикутник зі сторонами 13, 14 і 15 см обертається навколо середньої сторони. Знайдіть об’єм тіла обертання. 3. Ромб зі стороною а і гострим кутом а обертається навколо однієї із сторін. Знайдіть повну поверхню тіла обертання. |
1. Прямокутний трикутник з катетом а і прилеглим гострим кутом а обертається навколо гіпотенузи. Знайдіть площу поверхні і об’єм тіла обертання. 2. Трикутник з і сторонами 11, 25 і 30см обертається навколо меншої сторони. Знайдіть об’єм тіла обертання. 3. Прямокутна трапеція з основами а і с (а<с) і гострим кутом а обертається навколо меншої сторони. Знайдіть повну поверхню тіла обертання. |
|
Варіант В 1 |
Варіант В 2 |
|
1. Паралелограм, площа якого дорівнює 18см2, обертається навколо сторони, яка дорівнює 6см. Знайдіть об’єм тіла обертання. 2. рівнобедрений трикутник з бічною с і кутом при основі а обертається навколо прямої, яка лежить у площині трикутника і проходить через вершину кута а перпендикулярно до бічної сторони трикутника. Знайдіть площу поверхні і об’єм тіла обертання. |
1. Ромб з площею 18см2і гострим кутом 300обертається навколо сторони. Знайдіть об’єм тіла обертання. 2. Рівнобедрений трикутник з бічною стороною а і кутом при вершині а обертається навколо прямої, яка проходить через вершину кута при основі перпендикулярно до основи трикутника і лежить у площині трикутника. Знайдіть площу поверхні і об’єм тіла обертання.
3. Круговий сектор радіуса R з довжиною дуги |
Оцінювання
• рівень А – 4 бали,
• рівень Б – 6 балів,
• рівень В – 9 балів.
Примітка: не обов’язково оцінювати кожного учня за правильне розв’язання кожного рівня – на розсуд вчителя, може бути оцінений лише один із рівнів.
Тема: Ознака перпендикулярності прямої
і площини
Хід уроку
ІV Закріплення нового матеріалу
Цей етап уроку пропонується провести у вигляді математичного диктанту. Для цього група поділяється на 2 підгрупи: 1 варіант і 2 варіант. Завдання з’являється на дошці за допомогою мультимедійного проектора.
Відрізок МА перпендикулярний до площини АВС
Варіант 1 Варіант 2
|
|
|
прямокутника АВСD ромба CBDF
в якому АВ= 3см, AD=4см, MA=1см
Користуючись зображенням, знайдіть:
1) відстань між точками М і В,
2) довжину відрізка MD,
3) відстань між точками А і С,
4) довжину відрізка BD,
5) відстань між точками М і С,
6) площу трикутника МАС.
Після закінчення часу на виконання роботи відбувається перевірка правильності виконання математичного диктанту. По одному учневі з кожного варіанта виходять до дошки і пояснюють хід розв’язання кожного завдання.
Оцінювання
• за кожну правильну відповідь – 1 бал
Висновки
Основною формою організації навчальної діяльності практично в усіх країнах світу є класно-урочна система. Але будучи прогресивною протягом чотирьох століть, вона перестала задовольняти потреби суспільства в освіті і потребує вдосконалення. Критика такої системи найчастіше пов’язана з пасивністю учнів на уроках та відсутністю інтересу до навчання, зниження якості знань, перевантаження дітей домашніми завданнями.
Саме по собі навчання не повинно бути автоматичним вкладанням навчального матеріалу в голову учня. Він потребує напруженої розумової роботи дитини і її власної активної участі в цьому процесі. Пояснення й демонстрація, самі по собі, ніколи не дадуть справжніх, стійких знань.
У результаті спостережень за організацією навчання із використанням різних моделей навчання: активної, пасивної (за Я.Голантом) та інтерактивної (за О.Пометун) можна зробити висновки:
• слухачі запам’ятовують 80% матеріалу, який опрацьовували та висловлювали самостійно та 90% усіх видів навчальної діяльності, в яких були задіяні (інтерактивні вправи);
• поліпшується не тільки запам’ятовування матеріалу, але й його ідентифікація, використання повсякденному житті;
• робота в малих групах сприяє розвитку таких особистісних якостей, як комунікабельність, співробітництво, уміння відстоювати свою точку зору, йти на компроміси і т.д.
Таким чином, використання інтерактивних технологій на уроках математики дає можливість збагачувати світоглядну і моральну основу суджень як окремої особистості, так і громадської думки учнівського колективу; є однією з найбільш гнучких форм включення кожного учня в роботу, забезпечує перехід від простих до складних завдань, вчить використовувати не готові завдання, а здобувати їх із власного досвіду, що веде до розвитку мислення – творчого і діалектичного. А найкориснішим у такому навчанні є те, що математика починає подобатися.
Перевірка й оцінювання результатів навчання сприяє формуванню в учнів оціночного ставлення до себе і своєї діяльності, виробляє почуття самокритичності, принциповості, а також таких рис характеру, як витривалість, наполегливість, уміння володіти собою. Необхідно створювати певні дидактичні умови для активного формування в учнів адекватної самооцінки, яка вважається серцевиною особистості, регулятором її поведінки і діяльності.
Контроль знань необхідний для забезпечення глибоких та міцних знань учня. Він виконує свою функцію, якщо носить різноманітний, диференційований, об’єктивний, систематичний та індивідуальний характер – все це дає змогу підвищити якість спільної роботи вчителя і учня.
Список використаних джерел
1. Бакулін С. Знаходження НСД і НСК натуральних чисел.
/ Математика, № 34 (382). - 2006. - с. 21-23.
-
Вареник Л.О. Деякі форми контролю на уроці математики //
Математика в школах України, № 2 (158). - 2007. - с. 35. -
Дремова І.А. Особистісна зорієнтованість контролю результатів
навчання алгебри в основній школі. // Дидактика математики: проблеми і
дослідження. Міжн. зб. наук, робіт. - Вип. 5 (15). - Донецьк, 2000. - с. 66-71.
4. Інтерактивні технології на уроках математики/ Укладач
І.С.Маркова. - X.: Вид. група «Основа», 2009. - 126 с.
-
Інтерактивні технології на уроках географії. - X.: Вид. група
«Основа», 2005. - 128 с. -
Пометун О.І. та ін.. Сучасний урок. Інтерактивні технології
навчання. - X.: Основа, 2005. - 124 с. -
Прохоренко СІ. Основні аспекти підготовки та проведення тестів.
//Математика в школах України, № 31 (223). - 2008. - с. 2-8.
8. Сафронюк Г.В. Методика проведення та захисту домашніх
контрольних робіт з математики в 10-11 класах. //Математика в школах
України, №33 (225).- 2008. -с. 11-14
1


про публікацію авторської розробки
Додати розробку