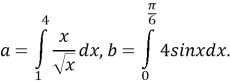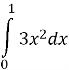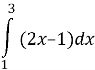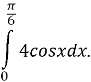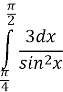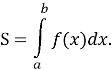Методичні матеріали до заняття на тему "Обчислення площ криволінійних трапецій"

№

Елементи заняття, питання, форми, методи навчання та засоби забезпечення заняття                                                                                                             

Доповнення

                                                                                                                                                                                                                                                                                                                                                                                                                                                  І.

Організаційна частина

1. Привітання.
2. Перевірка присутності студентів, їх підготовки до заняття.

ІІ.

Актуалізація опорних знань

1. Перевірка д/з.

1. Обчисліть:

a;  б)

2) Порівняйте числа a і b, якщо:

2. Вправа «Встанови відповідність».

Ми з вами готуємося до здачі ЗНО, тому я пропоную виконати наступне завдання:

ІІІ.

Мотивація навчальної діяльності студентів.

Інтеграл є невід’ємною складовою багатьох технічних та економічних процесів, які відбуваються навколо нас. Він має широкий спектр використання як в математиці, так і в інших сферах діяльності людини. Визначений інтеграл застосовують  розв’язуючи задачі, пов’язані з геометрією. Можливість розвивати ці уміння ви й матимете сьогодні. Це чудова  нагода закріпити і розвинути навички знаходити визначений інтеграл, застосовувати його при розв’язуванні задач, а саме, знаходженні площі криволінійної трапеції.

ІV.

Повідомлення теми, мети та плану заняття.

Тема: Обчислення площ криволінійних трапецій.

Мета: сформувати вміння використовувати визначений інтеграл для обчислення площ криволінійних трапецій.

План заняття

1. Поняття криволінійної трапеції.
2. Площа криволінійної трапеції.
3. Обчислення площі криволінійної трапеції за допомогою визначеного інтеграла.
4. Розв’язування задач.

V.

Сприймання і усвідомлення нового матеріалу.

В курсі геометрії ми вивчали як обчислити площу многокутників, круга та його частин. А як же обчислити площу плоскої фігури, обмеженої будь якою кривою?

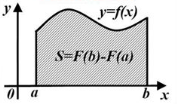
Нехай на проміжку задано неперервну функцію , яка на цьому проміжку набуває лише невід’ємних значень. Фігуру, обмежену графіком функції , віссю абсцис і прямими та , називають криволінійною трапецією.

Площу криволінійної трапеції можна знайти за допомогою визначеного інтеграла:

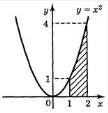
Приклад 1.

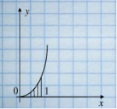
Обчисліть площу криволінійної трапеції, обмеженої графіком функції і прямими

Розв’язання.

Зобразимо на малюнку криволінійну трапецію.

Маємо: .

Відповідь: кв.од.

Приклад 2.

Обчисліть площу криволінійної трапеції, обмеженої графіком функції і прямими

Розв’язання.

Зобразимо на малюнку криволінійну трапецію.

Маємо: .

Відповідь: кв. од.

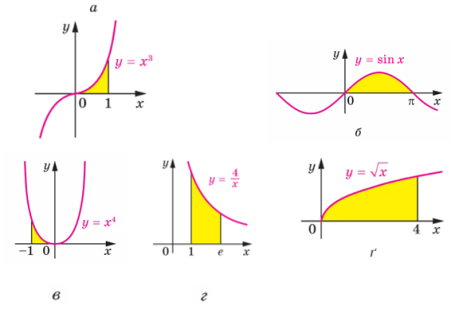
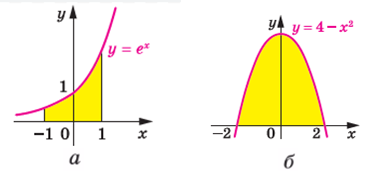
Приклад 3.

Запишіть за допомогою визначеного інтеграла площі фігур, зображених на малюнку:

колективно

самостійно

VІ.

Закріплення вивченого матеріалу.

Завдання 1.

Побудуйте схематично фігури, площі яких виражаються такими інтегралами:

а)      б) ;     в) ;    г) .

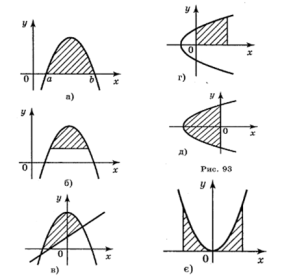
Завдання 2.

Запишіть за допомогою визначеного інтеграла площі криволінійних трапецій, зображених на малюнку:

        Завдання 3.

Обчисліть площу криволінійної трапеції, обмеженої графіком функції та прямою 0.                                                               

VІІ.

Узагальнення та систематизація знань студентів.

Експрес-тестування

• Дія, обернена до диференціювання …
• Первісні для однієї і тієї ж функції відрізняються тільки …
• Функція, записана під знаком інтеграла, називається…
• Множник dx означає…
• Криволінійною трапецією називається…
• Площа криволінійної трапеції дорівнює…
• Встановити, які із заштрихованих фігур є криволінійними трапеціями, а які - ні?

VІІІ.

Підведення підсумків.

1. Рефлексія.
2. Оголошення балів.

ІХ.

Домашнє завдання.

1. , № 11.5(1, 2, 5), № 11.7.
2. Творче завдання: підготувати проєкт або презентацію на тему «Обчислення площ криволінійних трапецій».