Методичні рекомендації "Математичне малювання"

Позакласна робота

МАТЕМАТИЧНЕ МАЛЮВАННЯ

 

                                                                                                  І.І. Придіус

 

Тема „Побудова графіків функцій та рівнянь” займає важливе місце в курсі  математики  оскільки, закладає основи аналітичного мислення, графічної культури, формує   інтуїцію, розвиває  уяву.  Найчастіше  у  школі   вивчення функцій обмежується будовою їх графіків за даними рівняннями. Але також дуже важливо вміти за відомими точками  графіка  написати  його  рівняння. 

Малюнки, в контурах яких є  лінії відомих елементарних функцій і рівнянь, називається математичним.

Якщо уважно придивитися навколо себе на  знайомі  нам  предмети, то можна побачити в них наближенні  контури  графіків  елементарних  функцій та ліній:  відрізки прямих,  кола, параболи, гіперболи і так далі. Коли йде мова про математичне малювання, то йдеться,  звичайно,  не  про  великі твори мистецтва, не про чудову гру фарб і багатство тонів, а тільки про малювання не складних фігур.

 Приклади малюнків, в контурах яких використані   графіки відомих елементарних функцій і рівнянь         

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

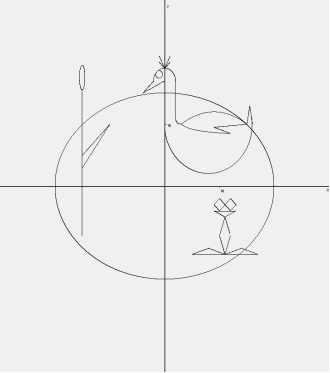
 Формули графіків функцій і рівнянь, які використані при  створенні  

 малюнків

1. «БІЛОЗЕРКА»

у=30, 1 ≤х ≤4;

у=28, 1 ≤х ≤4,35;

у=25, 1 ≤х ≤4,35;

х=1, 25≤ у ≤30;

(х-3)²+(у-26,5)²=4,

4≤ х≤ 5, 25≤ у≤ 28;

х=3, 18≤ у ≤22;

(х-3)²+(у-23)²= ;

у=2,5х+8,5, 1≤ х ≤3;

у=-2,5х+23,5, 3≤ х ≤5;

у=+6,5, 1≤ х ≤5;

у=-+6,5, 1≤ х≤ 5;

у=2, 2≤ х ≤4;

у=0, 2≤ х ≤ 4;

у=-3, 1≤ х ≤ 4;

(х-4)²+(у-1)²=1, 4≤ х≤ 5, 0≤ у ≤2;

(х-3,5)²+(у+1.5)²=2,25,

4≤ х ≤5, -3≤ у ≤0;

у=-5,  1≤ х ≤5;

у=-7,5,   1≤ х ≤ 5;

у=-10,   1≤ х ≤5;

х=1,   -10≤ у ≤ -5;

х=1,   -24 ≤у ≤-19;

х=4,   -20 ≤у ≤-19;

у=х-21, 1≤ х ≤4;

у=-0,75х-20,25, 1 ≤х ≤5;

у=-29, 2 ≤х ≤4;

у=2,5х-33,5, 1≤ х ≤3;

у=-2,5х-18,5, 3 ≤х ≤5.

 

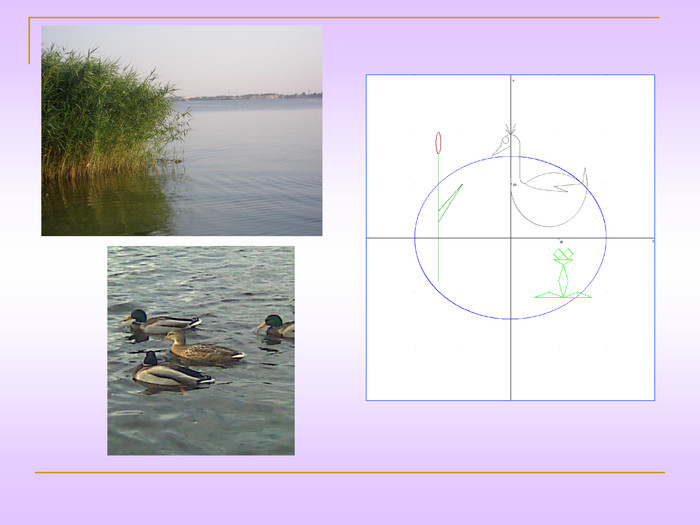
2. «ОЗЕРО»

 у=0,5х+17, -4≤ х ≤0;

 у=х+19, -4 ≤х ≤-2;

 у=+17, 0 ≤х≤ 2;

у=-+10, 0 ≤х ≤16;

у=-(х-9)²+12, 3 ≤х≤ 5;

у=+8, 3 ≤х ≤12;

у=6х-80, 15 ≤х ≤15,5;

у=-х+12,5, 9 ≤х ≤12;

 у=(х+105), 9 ≤х ≤15;

 у=‌‌‌+19, -1 ≤х ≤1;

 у=2+19, -1≤ х ≤1;

 у=-6х+106, 15,5 ≤х ≤16;

 +=1;

х=2, 11≤ у ≤17;

 (х-3)²+(у-1)²=1, 2 ≤ х ≤ 3, 10 ≤у ≤11;

(х+1)²+(у-18)²=0,38;

 х=-15, -8 ≤у ≤15,5;

 у=х+20, -15 ≤х ≤ -10;

 у=х+24, -15 ≤х ≤-10;

+=1;

| х-10| +|у+3|=1, 9≤  х ≤ 11,

 -4≤  у ≤ -2;

|х-12| +|у+3|=1, 11≤  х ≤ 13,

-4≤  у ≤ -2;

у=-4, 9 ≤  х ≤ 13;

у=0,5|х|-11-5, 9 ≤ х ≤ 13;

3|х-11|+|у+8|=3,10 ≤ х ≤ 12,

-11≤  у ≤ -5;

у=-11, 5≤  х ≤ 17;

у=|х-8|-10, 5 ≤ х ≤ 11;

у=|х-14|-10, 11≤  х ≤ 17.

3. «ЦЕРКВА»

у=-8, -18 ≤х ≤18;

=18, -8 ≤у ≤3;

=12, -8≤ у ≤3;

(х+15)²+(у-3)²=9, 3≤ у≤ 6;

(х-15)²+(у-3)²=9, 3≤ у≤ 6;

у=3, 6≤ ≤12;

=6, 3 ≤х ≤8;

у=8, -6≤ х ≤6;

(х+5)²+(у-8)²=1, -6≤ х ≤-5, 8≤ у≤ 9;

(х-5)²+(у-8)²=1, 5≤ х ≤6, 8 ≤у≤ 9;

х²+(у-9)²=25, -5 ≤х ≤1,4, 9 ≤у ≤13,4;

х²+(у-9)²=25, 1,4 ≤х ≤5, 9 ≤у ≤13,4;

=2,4, 13,4≤ х ≤15;

х²+(у-16)²=6.76, 15≤ у ≤18,6;

=15, 6≤ у≤ 9;

у=8, 14≤ ≤16;

=0,5, 18,6 ≤у≤ 21;

у=21, 0.6≤ ≤ 1;

=1, 21 ≤у ≤21,6;

=0,5, 21,6 ≤у ≤23;

у=23, -0.4≤ х≤ 0,6;

у=21,6, 0.5≤ ≤1,1;

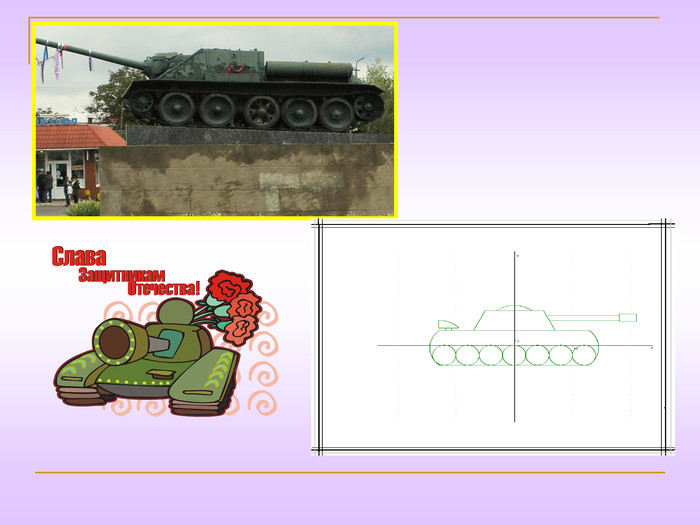
4.« ТАНК»

у=3,  -13≤ х ≤13;

у=-4, -13≤ х≤ 13;

(х-10)²+(у+0,5)²=20,25,

12≤ х ≤14,5, -4≤ у ≤3;

(х+10)²+(у+0,5)²=20,25,

-14,5≤ х≤ -12, -4≤ у≤ 3;

х²+(у+2)²=4;

(х-4)²+(у+2)=4;

(х-8)²+(у+2)=4;

(х-12)²+(у+2)=4;

(х+4)²+(у+2)=4;

(х+8)²+(у+2)=4;

(х+12)²+(у+2)=4;

у=2х+17, -7 ≤х ≤-5;

у=-2х+17, 5≤ х ≤7;

у=7, -5≤ х≤ 5;

 у=5, 6≤ х≤ 18;

 у=6,  5,5 ≤х ≤18;

 у=6,3, 18≤ х≤ 21;

у=4,8,  18≤ х≤ 21;

х=18, 4,8≤ х ≤6,3;

х=21, 4,8≤ х≤ 6,3;

х²+(у-3)²=25, 7 у 8;

у=3,5, -13≤ у≤ -9,5;

х=-13,  3,5 ≤у≤ 5;

х=-11,7, 3≤ у ≤3,5;

х=-10,7, 3 ≤у ≤3,3;

(х+13)²+у²=25,

-13≤ х≤ -9,5, 3,5≤ у≤ 5.

5 . «ПАМ'ЯТНИК»

у=3,1х-9,1, 1≤ х≤ 6;

у=9,5, 1,5 ≤х≤ 6;

у=-6, -2≤ х≤ 1;

у=-5, -4≤ х≤ -2,3;

у=-5, 1,4≤ х≤ 4;

у=-7, -5,5≤ х≤ 2,5;

у=-8,5, -5,5≤ х≤ 2,5;

х=-5,5, -8,5 ≤у≤ -7;

х=2,5, -8,5≤ у≤ -7;

х=4, -6,5≤ х≤ -5;

у=-х-, -5,75 ≤х ≤-2;

у=-+6, -5,75≤ х≤ -4;

у=х+, -5,5≤ х ≤-4;

у=х-, 2,5≤ х ≤4;

 у=х-, 2,5≤ х≤ 4.

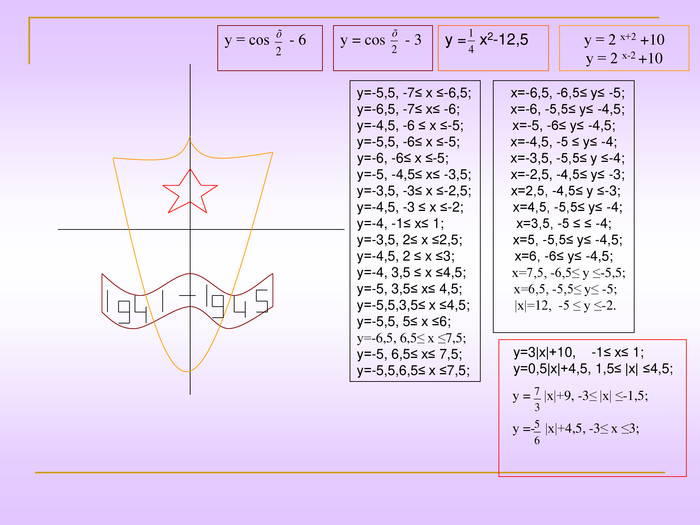
 6. «ЗНАК»

у= cos -6, -12≤ х≤ 12;                              

у=х²-12,5, -9,5≤ х ≤9.5;

у=3|х|+10, -1≤ х≤ 1;                                      

у=7, 1≤ |х|≤ 4,5;

у=0,5|х|+4,5, 1,5≤ |х| ≤4,5;

у=|х|+9, -3≤ |х| ≤-1,5;

у=-|х|+4,5, -3≤ х ≤3;

у=2^х+2 +10, -9,5≤ х ≤0;

у=2^х-2+10, 0≤ х ≤9,5;

у=-5,5, -7≤ х ≤-6,5;

у=-6,5, -7≤ х≤ -6;

х=-6,5, -6,5≤ у≤ -5;

у=-4,5, -6 ≤х ≤-5;

у=-5,5, -6≤ х ≤-5;

у=-6, -6≤ х ≤-5;

х=-6, -5,5≤ у≤ -4,5;

х=-5, -6≤ у≤ -4,5;

у=-5, -4,5≤ х≤ -3,5;

х=-4,5, -5 ≤у≤ -4;

х=-3,5, -5,5≤ у ≤-4;

у=-3,5, -3≤ х ≤-2,5;

у=-4,5, -3 ≤х ≤-2;

х=-2,5, -4,5≤ у≤ -3;

у=-4, -1≤ х≤ 1;

у=-3,5, 2≤ х ≤2,5;

у=-4,5, 2 ≤х ≤3;

х=2,5, -4,5≤ у ≤-3;

у=-4, 3,5 ≤х ≤4,5;

у=-5, 3,5≤ х≤ 4,5;

у=-5,5, 3,5≤ х ≤4,5;

х=4,5, -5,5≤ у≤ -4;

х=3,5, -5 ≤у≤ -4;

у=-5,5, 5≤ х ≤6;

х=5, -5,5≤ у≤ -4,5;

х=6, -6≤ у≤ -4,5;

у=-5, 6,5≤ х≤ 7,5;

у=-5,5, 6,5 ≤х ≤7,5;

у= cos -3, -12≤ х ≤12;

у=-6,5, 6,5≤ х ≤7,5;

х=7,5, -6,5≤ у ≤-5,5;

х=6,5, -5,5≤ у≤ -5;

 |х|=12,  -5 ≤у ≤-2.

7. «ЯЛИНКА»

 

у=-(|х| -3), 3≤ |х |≤8,5;

у=-(|х|-6), 1,5≤|х| ≤6;

у=-|х| +10,5, 0≤ |х| ≤3,5;

у=6, 1,5≤ |х| ≤3,5;

у=0, 3≤ |х| ≤6;

у=-8, 0 ≤ |х| ≤ 8,5;

у=-13,5, 0≤ |х| ≤0,5;

у=(х-12)²-10, 12≤ х ≤14;

у=-х-5, 10≤ х ≤12;

у=х-11, 12 ≤х ≤14;

у=0,75х-16, 11≤ х ≤12;

у=-0,75х+2, 12≤ х ≤13;

х=12, -13,5 ≤у≤ -10;

у=х-24, 12≤ х ≤14.

Основні види функцій  та рівняння ліній

 

1) у=kх – пряма пропорційність,

2) у=kх+в – лінійна,

3) у=- обернена пропорційність,

4) у=,

5) у=х², квадратичні,

6)у=ах²+вх+с,

7)  у=х³ –кубічна,

8) y=sinx,

9) y=cosx, тригонометричні,

10) y=tgx,

11) y=ctgx,

12) y=arcsinx

13) y=arccosx,     обернені тригонометричні,

14) y=arctgx,

15) y=arcctgx,

16) у=а^х –показникова,

17) у=log_ax –логарифмічна,

18) у= |f(х)|,

19) у= f(|х |), з модулями,

20)у= |f(|х|)|,

21) у=|х|,

22) х²+у²=R² ,                    коло

23) (х-а)²+(у-в)²=R² ,

24) х=а – пряма паралельна осі оу,

25)   + =1-еліпс.

 

Переведення малюнків на мову формул

Розглянемо конкретний приклад. Переведемо малюнок “ЗНАК” на мову формул. Він спрощений і значно відрізняється від того зображення, яке б подав справжній художник. Але кожному, хто дивиться на малюнок, ясно, що він зображає.

   Перший етап – вибір системи координат. Навіть, при довільному розташуванні координатних осей можна записати рівняння, які відповідають лініям малюнка. Але потрібно прагнути до того, щоб кількість рівнянь, які описують малюнок, була якнайменшою, а самі рівняння – якомога простішими. Наприклад, на малюнку “Знак” є відрізки симетричні відносно осі OY та ОХ. Це дасть можливість їх описувати не двома, а одним рівнянням. Отже, вибір координатної системи відіграє велику роль при програмуванні малюнків.

   Другий етап. Насамперед опишемо рівняннями ті ділянки малюнка, які мають вигляд відрізків, паралельних осям координат. Для цього кінці кожного  цих відрізків спроектуємо на вісь OY та ОХ .Отже, таким способом визначаються рівняння всіх зазначених ділянок та множини тих значень, яких набувають змінні  х і у. Відрізки, які паралельні осі OY , мають вигляд: х=а, а відрізки, паралельні осі ОХ :  у=а.

    Наприклад, рівняння такої складової частини нашого малюнка як цифра один, такі:

              у = -5,5,  де     -7 ≤ х ≤ -6,5;

              у = -6,5,  де     -7 ≤ х ≤ -6; 

              х = -6,5,  де      -6,5 ≤ х ≤ -5.                      

    Тепер перекладемо на мову рівнянь відрізки, які не паралельні осям координат.

      Як відомо, така пряма є графіком лінійної функції. Отже, рівняння кожного з зазначених відрізків представимо у вигляді:

                                   у = кх + b,                                                (1) 

де х і у –змінні, а к і b – невідомі параметри, які залежать від розташування прямої на координатній площині. Параметр к – кутовий коефіцієнт прямої – визначається кутом, який утворює ця пряма з віссю абсцис, а b – відрізок, який зазначена пряма відтинає від осі ординат. Для знаходження рівняння  відрізка, що належить прямій, яка   не паралельна осям координат використаємо декілька способів.

   Перший спосіб.

1. Продовжимо даний відрізок до перетину з віссю OY.  Ордината точки перетину є параметр b.

2. Зафіксуємо точку відрізка і визначимо її координати х₀ і у₀.

3. Шукані числа х₀, у₀ і b підставимо в рівняння (1).

4. З утвореної рівності  у₀= кх₀ + b знайдемо другий невідомий параметр: k= .

   Наприклад, розглянемо відрізок з областю визначення [-4,5;-1,5]. Продовжимо  його до  перетину з   віссю OY. В даній точці у = 4,75, отже b=4,75.  Зафіксуємо на даному  відрізку  точку  (-1,5; 5,5).  Знайдемо коефіцієнт к: k= = -=-0,5. Отже   маємо рівняння відрізка: у=-0,5х+4,75, де

-4,5 ≤ х ≤ -1,5.

   Другий спосіб.

      У таких випадках, коли визначення параметра b пов'язане з певними труднощами (наприклад, тоді, коли точка перетину продовження даного відрізка з віссю OY  виходить за межі аркушу паперу, на якому зображений малюнок), зробимо  інакше, а саме: 

  1. Зафіксуємо дві довільні точки даного відрізка і визначимо їх координати.

  2. Знайдені числа х₁, у₁ і х₂ ,у₂ підставимо і формулу:

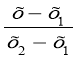                                        =                                (2)

що є рівнянням прямої, яка проходить через дві дані точки (х₁; у₁) і (х₂; у₂). При цьому параметри к і b, очевидно, будуть такі самі, як і ті, що були знайдені першим способом.

   Наприклад, зафіксуємо точки (-1,5; 5,5) та (-4,5; 7), що є кінцями даного відрізка. Підставимо їх у формулу (2):

=;

=;

1,5(х+1,5)=-3(у-5,5);

1,5х+2,25=-3у+16,5;

1,5х+3у=16,5-2,25;

1,5х+3у=14,24;

у=;

у=-0,5х+4,75.

    На малюнку "Знак", який ми розглядаємо,  є відрізок симетричний відносно осі Y  відрізку рівняння якого ми записали. Тільки область значень змінної х є проміжок [1,5; 4,5]. Так як при протилежних значеннях змінної х змінна у приймає одне й те саме значення, то в рівнянні відрізка замінимо х на‌‌‌ │х‌‌‌‌│. Отже, щоб скласти рівняння будь – яких двох ділянок малюнка, симетричних відносно осі ординат, треба:

1.Скласти рівняння відрізка, що лежить у правій півплощині.

2.Замінити в цьому рівнянні змінну координату х на‌‌‌│х‌‌‌‌│.

    Тоді рівнянь двох відрізків симетричних відносно осі Y, має вигляд:

 у= 0,5│х‌‌‌‌│+ 4,75, де   1,5 ≤ │х‌‌‌‌│ ≤ 4,5. 

       Дещо складніше перекласти на мову формул ті частини малюнка, які мають вигляд параболічних кривих. Отже, опишемо рівнянням лінію, яка є основою нашого знака.

       Оскільки ми маємо справу з параболою, вісь симетрії якої паралельна осі  OY, то рівняння цієї параболи слід шукати у вигляді:

                                 y= k (х + а) ² + b

де, у і х – змінні координати, а k , а і b – невідомі параметри, що залежать від розташування параболи на координатній площині. Зауважу, що числа а і b визначаються координатами вершини параболи, а сама вершина параболи  має координати (-а; b). Параметр к можна знайти з рівності y=  k (х + а) ² + b, коли замість змінних координат підставити координати деякої фіксованої, відмінної від вершини точки (х₀;  у₀) параболи. Маємо:

               у = .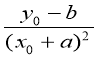               

      Наприклад, визначаємо за графіком координати вершини параболи (0; -12,5) та деякої фіксованої точки (2; -11,5). Знаходимо параметр k :

            k= =.

Таким чином рівняння параболи має вигляд:

                                                               у=х²-12,5,де -9,5 ≤х ≤9,5.

  Верхня частина малюнка «ЗНАК» складається з двох частин, кожна з яких є графіком показникової функції, формула якої у=а^х, де  а>0, а≠1. Якщо графік функції зміщено по осі ОХ і осі ОУ, то формула приймає вигляд у=а^х+m+n.

Розглянемо спочатку графік, розміщений у правій півплощині

Зафіксуємо на ньому декілька точок: (0,14);(-2,11);(-1,12). Підставимо їх координати у формулу та отримаємо систему трьох рівнянь з трьома невідомими:

    a^0+m+n=14,

    a^-2+m+n=11,

    a^-1+m+n=12;

   

    a^m=14-n,

    a^-2+m=11-n,

    a^-1+m=12-n;

     a^m=14-n,

    (14-n)(a^-1)²=11-n,

    (14-n)a^-1=12-n;

a^-1=,  a^-2==, 

=11-n, (12-n)²=(11-n)(14-n),

144-24n+n²=154-11n-14n+n²,

-24n+11n+14n=154-144,

n=10.

Підставимо знайдене значення n в друге рівняння системи.

a^m-2+10=11, a^m-2=1, a^m-2=а⁰, m-2=0, m=2.

Підставимо знайдені значення m і n в перше рівняння системи.

а²+10=14, а²=4, а=2 і а=-2. Врахуємо область допустимих значень а.

Отже, у=2^х+2+10.

Друга частина графіка симетрична відносно осі ОУ і спадає. Тоді її формула: у=()^х-2+10.

Тепер розглянемо ділянку малюнка, що має вигляд хвилі. Оскільки графік симетричний відносно осі, то його основою є косинусоїда формула якої  у= cosх,   з періодом  2П≈ 6,28. Визначимо період функції на даному малюнку: Т=12,5. Це означає, що косинусоїду стиснуто вздовж осі  Y  в 2 рази, отже її рівняння : y=cos. Також ми бачимо, що графік паралельно зміщено вздовж осіY на 3 одиниці вниз, отже кінцева формула графіка ділянки нашого малюнка має вигляд   y=cos-3.

  СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ТА ЛІТЕРАТУРИ

1. Гурский И.П. Функции и построение графиков. - М.:Просвещение, 1968.- С. 

    215.

2. Математика. Вип. 5 (113).- К.: Шкільний світ, 2001.- С.15.

3. Сивашинский И. Х. Элементарные функции и графики. – М.:Наука,1966. –  С.117

4. Скоблев Г.М., Берман В.П.  Математика в позаурочний час. – К.: Рад.  школа, 1973. – С. 153 – 157.

5. Скоблев Г. М., Берман В. П.   Математика допомагає малювати. У світі 

     математики. Вип. 2. – К.: Рад. школа, 1970.

6.  Шунда Н. М. Функції та їх графіки. – К.:Рад. школа, 1983. – С. 190.   

7. Яремчук Ф. П., Рудченко П. А.   Алгебра и єлементарные  функции.     Справочник. – К.: Наукова думка , 1976. – С. 686.

 

Додаток. Презентація Power Point