Множення двох раціональних чисел з різними знаками.
Тема. Множення двох раціональних чисел з різними знаками.
Мета: сформувати уявлення про зміст дії множення двох раціональних чисел з різними знаками та виробити вміння використовувати цей алгоритм для обчислення значень виразів.
Тип уроку: застосування знань, умінь і навичок.
Хід уроку
І. Перевірка домашнього завдання
1) Математичний диктант
Варіант 1 [2]
- Запишіть у вигляді виразу добуток -3 та -4 [-5 та -7].
- Виконайте множення:
а)-5 на -8 [-7 на-9]; б) -![]() на -4 [-15 на -
на -4 [-15 на -![]() ]; в) -5,3 на -0,1 [-0,01 на -23].
]; в) -5,3 на -0,1 [-0,01 на -23].
-
Порівняйте добутки: -2,3 і -7,3 та 2
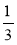 і 7
і 7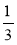 [-3
[-3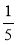 і -
і -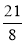 та 3,15 і +2,1].
та 3,15 і +2,1].
Під час перевірки результатів виконання математичного диктанту повторюємо правило множення двох чисел з однаковими знаками.
II. Актуалізація опорних знань
Усні вправи
- Прочитайте вирази: а) 11·12; б) 11·12 + 5; в) 11·(12 + 5); г) 11·(12 - 5).
- Обчисліть: а) 10 · 15; б) 11 · 12; в) 24 · 5; г) 24 · 25; д) 25 · 16 (використовуючи прийоми швидкої лічби).
-
Замість * поставте знак «>» або «<», щоб нерівність стала правильною,
а) -7 · (-3) * 0; б) -7 · (-3) * 10 · 2; в) -7 * 10 · 2.
III. Формування знань
Задача 1. Температура повітря знижується щогодини на 2 °С. Зараз термометр показує 0 °С. Яку температуру повітря буде показувати термометр через 3 год?
Розв'язання. Оскільки зараз температура 0 °С, і щогодини вона знижується на 2 °С, то через три години вона буде -2 + (-2) + (-2) = -6 градусів. Цей самий результат можна було дістати, позначивши погодинне зниження температури як -2 °С, а наступний час + 3 год й виконати дію: (-2) · (+3) = -6.
Отже, (-2) • (+3) = -6. (1)
Задача 2. Зараз температура повітря 0 °С і щогодини вона підвищується на 2 °С. Яку температуру показував термометр 3 год тому?
Розв'язання. Оскільки зараз 0 °С, і щогодини температура підвищувалась на 2 °С, то зрозуміло, що три години тому вона була -6 °С. Цей же самий результат можемо дістати, позначивши щогодинну зміну температури як+2 °С, а час, що пройшов, -3 год (ми «повертаємось» у часі назад). Тоді маємо:
+2 · (-3) = -6. (2)
Можна розглянути кілька наочних прикладів, записати рівності, подібні до (1) та (2), і порівняти їх, діставши такий висновок: Щоб помножити два числа з однаковими знаками, треба:
- перемножити їх модулі;
-
перед результатом поставити знак «-»,
тобто:
Добуток двох чисел з різними знаками є число від'ємне; модуль цього числа дорівнює добутку модулів даних чисел.
Наприклад
а) -8 · (+5) = -(|-8| · |+5|) = - (8 · 5) = -40,
можна писати коротко (модулі обчислювати усно):
-8 · (+5) = - (8 · 5) = -40;
б) +1,7 · (-5) = - (1,7 · 5) = -8,5.
Зауваження. Під час множення як і під час додавання раціональних чисел спочатку можна визначати знак результату, а потім вже виконувати дію з модулями.
IV. Закріплення знань. Вироблення вмінь
Усні вправи
- Прочитайте рівності. Чи є вони правильними?
а) -3 · (-2) = -6; б) -3 · (+2) = +6; в) +3 · (-2) = -6; г) -(+3) · (-2) = 6.
- Який знак має добуток?
а) -3 · (-1,5); б) 9 · (107); в) -![]() · 0,5; г) а · b, якщо а > 0, b < 0?
· 0,5; г) а · b, якщо а > 0, b < 0?
-
Обчисліть: а) -4 · (-10); б) -7 · (+6); в) +8 · (+0,02); г)
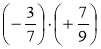 ;
;
д) 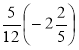 ; є) -0,01·(-0,1); ж) -0,1·(+9).
; є) -0,01·(-0,1); ж) -0,1·(+9).
Письмові вправи
На цьому уроці ми вже виконуємо вправи на множення як чисел з однаковими знаками, так і чисел з різними знаками. Але, як і на попередньому уроці, кожного разу вимагаємо відтворення відповідного алгоритму.
- Виконайте множення: а) 11·72; б) -11 · (-72); в) -11 · 72; г) 11 · (-72). Звернути увагу на те, що, обчисливши добуток модулів (у п. а), у наступних прикладах ми повинні тільки визначити знак добутку і поставити його перед добутком модулів (повторюємо алгоритм усного множення двоцифрового числа 1).
- Виконайте множення:
а) -16 · 2,5; б) 0,01 · (- 65); в) -100 · 0,02; г) -4 · (-10,5);
д) -5 · 3![]() ; є)
; є) ![]() ·
·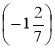 ; ж) -3
; ж) -3![]() ·
·![]() ; з) 5,6 ·
; з) 5,6 · ![]() .
.
Перед виконанням дій вимагати від учнів аналізу того, із яким саме випадком множення маємо справу.
- Обчисліть: а) -16 + 8 · (-0,5); б) -2 · (-1,8 – 1,2); в) -8 · 0,5 + 5 · (-0,6);
г) 5![]() ·
·![]() + 6; д) -
+ 6; д) -![]() +
+![]() ·
·![]() ; е)
; е) ![]() ·
·![]() -
-![]() ·
·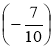 .
.
Перед виконанням дій вимагати:
а) визначити правильний порядок виконання дій;
б) повторити алгоритми множення та додавання раціональних чисел.
- Поставте замість зірочки знак «<» або «>» так, щоб утворилась правильна нерівність: а) 100 · (- 3) * 300; б) 0,2 · (-14) * -2,5.
Додаткові вправи
- Обчисліть:
а) (- 7,6 - 5,8 + 4,5) · (6,3 - 8,2); б) -2,69 · (-0,8) + 0,7 · (4,3 - 7,8);
в) -10,8 · (-7,6 - 6,8) · (-3,5); г) (- 7,65 · (- 0,4) - 5) · (3 - 1,02);
д) (- 2,36 + 6,82 - 5,45) · (46,5 - 91,5) + (- 45,09).
-
Обчисліть: а) 5,6 ·
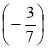 - (-5) · 3
- (-5) · 3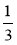 ; б) -0,75 ·
; б) -0,75 · 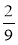 - 7
- 7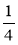 · (-0,3);
· (-0,3);
в) (-3,4) · 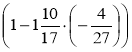 ; г)
; г) 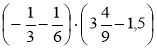 .
.
Більш складні завдання на сумісні дії множення і додавання раціональних чисел.
- Логічна вправа (на повторення)
Знайдіть і поставте замість (?) пропущений рисунок:
|
|
|
|
|
|
|
|
? |
V. Підсумок уроку
-
Як виконати множення двох чисел, якщо вони
а) з однаковими знаками, б) з різними знаками? -
Що більше добуток двох чисел з однаковими знаками чи добуток
двох чисел з різними знаками? -
Замість * поставте знаки «+» або «-», щоб рівності стати правильними
а) *5 · *2 = -10; б) *5 · *2 = 10; в) (-5) · (-2) = *10.
VI. Домашнє завдання
Усні вправи
- Обчисліть а) 8 · 6; б) 8 · (- 6); в) -8 · 6; г) -8 · (-6); д) 7 · (-4); є) (-7) · (-4);
ж) -5 · 4; з) -100 · 0.
-
Обчисліть а) - 0,2 ·3; б) 2 · (-0,6); в) (-1,2) · (-2), г) -0,1 · (-20).
Письмові вправи
- Виконайте множення а) -12 · 25; б) 1,3 · (-5); в) -10 · (-70,1),
г) -5,45 · (-1,02); д) 105 · (-0,18); є) 12 · ![]() ; ж) -
; ж) -![]() ·
· 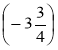 ; з) -4
; з) -4![]() · 1
· 1![]() .
.
- Обчисліть а) - 0,4 · (-10) – 7; б) - 0,3 · 1,2 - 2,5; в) (0,1 - 0,6) · 8;
г) -0,7 · 6 + 7,2 · 0,2, д) 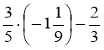 ; є)
; є) 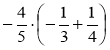 .
.
-
Обчисліть 1,2 · (-6,39 + 4,84) -
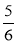 · 24,6.
· 24,6.
Вправа на повторення
На першій книжковій полиці на 60 книжок більше, ніж на другій Скільки книжок на кожній полиці, якщо кількість книжок на другій полиці становить ![]() кількості всіх книжок?
кількості всіх книжок?


про публікацію авторської розробки
Додати розробку
