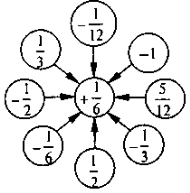
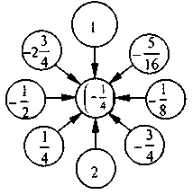
Множення та ділення раціональних чисел
Тема. Множення та ділення раціональних чисел
Мета: підготувати учнів до виконання тематичної контрольної роботи.
Тип уроку: узагальнення та систематизація знань.
Хід уроку
I. Перевірка домашнього завдання
Усні вправи
- Обчисліть:
|
а) |
|
б) |
|
- Обчисліть, вибравши зручний порядок дій:
а) (-5) · (-6) · 7; б) (-1) · (-5) · (-8); в) (-12) · 5 · 0 · (-6); г)  ;
;
д) (-0,2) · (-0,2) · (-0,2) · (-0,2); є) 1,2 · ![]() ·(-1,8)·
·(-1,8)·![]() .
.
-
Назвіть коефіцієнт виразу: -0,5ab; ab; -cb; -abc;
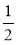 ab; -
ab; -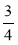 ху; 1,7mn ; -2,3х.
ху; 1,7mn ; -2,3х.
- Назвіть подібні доданки в сумі та їх коефіцієнти:
a) 5a - 7a + 8b - 2b; б) 3х – 4y + 8,2х - 5![]() у;
у;
в) -15х + у – х – у; г) -2![]() b – 1 – b + 8b.
b – 1 – b + 8b.
Зведіть подібні доданки.
- Розв'яжіть рівняння:
а) 3 · х = 0; б) 3 · (х - 0,5) = 0; в) 3 · (3х + 0,3) = 0; г) х · (3х + 0,3) = 0.
II. Систематизація знань
На цьому уроці ми «підбиваємо підсумки» з приводу вивчення теми «Множення раціональних чисел» («Ділення раціональних чисел» ми розглянемо на наступному уроці). Тому хотілося, щоб на уроці прозвучали основні теоретичні викладки, пов'язані з цією темою (алгоритми множення раціональних чисел, властивості множення раціональних чисел тощо). Але, щоб не перетворювати цей урок на нудне опитування, бажано провести цей етап в ігровій формі (наприклад, брейн-рингу, де учні групуються по 4-5 осіб, або у вигляді інтелектуального аукціону (методику проведення дивись у додатках)).
III. Відтворення, вдосконалення та корекція вмінь
Після проведеної систематизації знань (див. вище) дуже важливо перевірити практичні вміння учнів, тому особливу увагу звертаємо на розподільну властивість множення (зведення подібних доданків в алгебраїчних сумах та перетворення цілих виразів у алгебраїчну суму із застосуванням розподільної властивості множення) та сполучну властивість множення і властивість нуля при множенні. Відповідно підбираємо завдання.
- Обчисліть значення виразу.
а) 34 · (-4); -7,2 · (-7); -2,6 · 3,4; -32,15 · (-0,6); -3![]() ·1
·1![]() ; -3
; -3![]() ·
·![]() .
.
б) -14,3 · 0,6 + 5,7 · (-1,4); (23,42 - 54) · (-4,12 + 4,04);
в) ![]() ·
·![]() -
-![]() ;
; ![]() .
.
- Використавши сполучну властивість множення:
1) обчисліть:
а) -5,49 · 4; б) -125 · 17 · (-0,8); в) 0,4 · (-25) · (-5) · (-0,2);
г) -3,73 · 50 · (-2) · (-0,01); д) ![]() ·(-4,5)·
·(-4,5)·![]() ·0,4;
·0,4;
є) -![]() ·
·![]() ·
·![]() ·(-22);
·(-22);
2) спростіть вираз:
а) -1,2 · 3а; б) -0,8х · (-0,7); в) -5b · 2,4с; г) -6а · 0,7b · (-0,5с);
д) -![]() x ·
x · ![]() · (-y); є) 1
· (-y); є) 1![]() x ·
x · ![]() ;
;
3) спростіть вираз -0,5т - 20п і знайдіть його значення при
т = -1![]() ; n = -2
; n = -2![]() .
.
- Використовуючи розподільну властивість множення:
1) розкрийте дужки:
а) 2(х - 7у + 3z); б) -7(5 – a – 4b); в) (с – 8d + 66)·(-1,2);
г) -0,6х(-5 + 3m - 1,4n); д) -р(-х + 2у -4,6); є) -8![]() ;
;
2) зведіть подібні доданки:
а) 8а + 19а - 28а + 3а; б) -4х + 11х + 35х – 38x, в) 1,4а – a + b - 2,6b;
г) 1,6m - 1,2 - 3,1m + 0,8; д) 1,1p + 0,9d – 1,2 - 1,3p - 3,8d;
е) -![]() a +
a + ![]() b +
b + ![]() a -
a - ![]() b;
b;
3) розкрийте дужки і зведіть подібні доданки:
а) 7(4а + 6) - 12а; б) 8х - 4(16 - 2х); в) 1,7(а - 4) + 0,6(6 - 2а);
г) 1,5(8x – 6y) - (5y - 3x) · 2,4; д) -(4,3х - 2,4) - (5,8 - 2,6х);
є) ![]() .
.
Додаткові вправи
Знайдіть значення виразу: 1) 0,6(4х - 12) - 0,4(5х - 7) при х = 4![]() ;
;
2) 5![]() (y - 7) - 3
(y - 7) - 3![]() (14 - y) при y = -0,4.
(14 - y) при y = -0,4.
IV. Підсумки уроку
Звертаємо увагу на ті моменти, що викликали труднощі під час розв'язування вправ.
V. Домашнє завдання
-
Виконайте дії: а) (- 5 + 4,8) · (- 0,5)2; б) (8 - 10,2) · (- 9 + 7,5);
в) (- 7 - 8 + 16,1)2; г) (- 2,75 + 3) · (- 0,2)2. -
Виконайте дії:
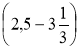 · (1,2 - 1,8).
· (1,2 - 1,8).
-
Спростіть вираз: а) (2a - 5) - (4 – 7а); б) -(-6 - 4х) + 2(-8х + 3);
в) (6x - 4y + 1) - (-2x + 3y - 5); г) 0,5(8 - 4а) - 3(0,2а - 1);
д) (1,2a - 1,8b + 3)·(-2) - 5(1,2a + 1,8b – 1,3); є) ![]() ·
·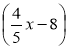 -4·
-4·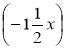 .
.
-
Знайдіть значення виразу -3
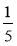 x ·
x ·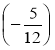 y; якщо х =
y; якщо х = 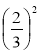 , у =
, у = 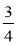 ..
..

про публікацію авторської розробки
Додати розробку