Наукова робота «Диференційоване навчання алгебри учнів основної школи»
Питання диференційованого навчання на сучасному етапі розвитку школи є найбільш актуальним та доцільним. Головна мета диференціації – це забезпечити базовий рівень знань кожному учневі, а здібним учням – надати можливість глибше опанувати предмет. Тобто, прикладний рівень – для всіх учнів, творчий – для здібних.
1
«Диференційоване навчання алгебри учнів основної школи»
ЗМІСТ
РОЗДІЛ І. ДИФЕРЕНЦІЙОВАНЕ НАВЧАННЯ МАТЕМАТИКИ. ОСНОВНІ ПОНЯТТЯ ТА ПІДХОДИ
1.1. Психолого – педагогічні особливості учнів 7 – 9 класів
1.2. Поняття диференційованого навчання в педагогіці та методиці
1.3. Аналіз програм і підручників з алгебри для 7 – 9 класів у контексті дослідження
РОЗДІЛ ІІ. РЕАЛІЗАЦІЯ ПРИНЦИПУ ДИФЕРЕНЦІЙОВАНОГО НАВЧАННЯ НА УРОКАХ АЛГЕБРИ В ОСНОВНІЙ ШКОЛІ
2.1. Використання диференційованого підходу на різних етапах вивчення матеріалу
2.2. Методичні розробки уроків з теми «Квадратні рівняння» (алгебра, 8 клас)
ВСТУП
Актуальність дослідження. У нашій країні спостерігаються зміни по відношенню до загальнолюдських цінностей, до знань, зокрема існує відмінність у поглядах на освіту представників різних поколінь. Доросле покоління розуміє необхідність отримання освіти, як залог майбутньої економічної самостійності, на відміну від молодших поколінь, у яких інтерес до навчання знизився. На сьогоднішній день, на наш погляд, не дивлячись на гостру необхідність у кваліфікованих фахівцях, економічна підтримка освіти з боку держави є недостатньою. Із досвіду вчителів: реформи у галузі освіти та напрямки школи не завжди відповідають інтересам самих школярів. На жаль, є діти, які бажають отримати знання та вміння, керуючись лише споживацькими цілями. Причому у школярів спостерігається вибірковий інтерес до предметів. Великою популярністю (через необхідність здавати ЗНО) користуються математика, англійська мова та інформатика. Перед школою стоїть завдання – підвищити інтерес учня до навчання, що є ключовим фактором інтелектуального розвитку особистості.
Для успішного виконання поставлених завдань, необхідна зміна підходів до навчання школярів у реальному процесі навчання, а отже переорієнтація вчителів. Як показує аналіз літератури [10; 18 – 21; 25 – 27], можливим виходом із наявної ситуації може бути реорганізація роботи школи, в основі якої лежать умови врахування індивідуальних особливостей школярів.
На сьогоднішній день, особистісно-розвивальну спрямованість освіти неможливо здійснити без диференційованого навчання. Найбільш зручною та діючою для кожного вчителя є диференціація у класі, в якому навчаються учні з різним рівнем знань, яка спрямована як на допомогу учням, що мають прогалини у знаннях, так і на розвиток творчих здібностей в учнів, які вільно володіють матеріалом. За допомогою використання диференційованого підходу робота на уроці дає можливість вчителю одночасно працювати з усіма учнями. Учні, які швидше розуміють матеріал, поглиблюють свої знання та допомагають іншим, а ті, в кого знання на нижчому рівні, міцно засвоюють програмний матеріал. Завдання можна варіювати та розподілити за рівнем знання кожної дитини. Актуальність проблеми диференційованого навчання на сучасному етапі розвитку школи полягає ще в тому, що вчитель має знати: рівень підготовки і рівень розвитку кожного учня, його індивідуальні особливості.
Дана тема була досліджена багатьма авторами, наприклад Ю. К. Чабанським, Ю. М. Колягіним, З. І. Слєпкань, М. І. Махмутовим, , Р. С. Черкасовим, І. Е. Унт, О. Я. Савченко, С. П. Логачевською та інші, але з розвитком суспільства змінюються i вимоги, і структура організації диференційованого навчання, а це не може не відобразитися на вихованні та розвиткові дітей. Тому темою дослідження обрано: «Диференційоване навчання алгебри учнів основної школи».
Мета дослідження: на основі вивчення психолого-педагогічних особливостей учнів 7 – 9 класів, різних підходів по впровадженню диференційованого навчання, розробити елементи методичної системи диференційованого навчання алгебри учнів основної школи.
Завдання дослідження:
- Вивчити психолого-педагогічні особливості учнів 7 – 9 класів.
- Проаналізувати різні підходи до визначення диференційованого навчання в педагогіці та методиці.
3. Проаналізувати програм та підручників з алгебри у контексті дослідження.
4. Розглянути основні шляхи використання диференційованого навчання на різних етапах уроку.
5. Розробити конспекти уроків з теми «Квадратні рівняння», основані на використанні диференційованого підходу.
Об’єкт дослідження: процес навчання алгебри учнів основної школи.
Предмет дослідження: методика диференційованого навчання алгебри у основній школі.
Практичне значення дослідження. Практичне значення дослідження полягає в тому, що авторські методичні розробки можуть бути використані вчителями математики, студентами педагогічних університетів для налагодження диференційованого навчання та формування творчої особистості учнів на уроках.
РОЗДІЛ І. ДИФЕРЕНЦІЙОВАНЕ НАВЧАННЯ МАТЕМАТИКИ. ОСНОВНІ ПОНЯТТЯ ТА ПІДХОДИ
1.1. Психолого – педагогічні особливості учнів 7 – 9 класів
Успішне засвоєння матеріалу з предмету на уроках та ефективне проведення позакласних заходів можливе тільки у разі врахування особливостей навчання та вікових характеристик учнів-підлітків, визначення необхідних прийомів, форм та засобів навчання.
Кожен віковий період визначається особливим етапом психічного розвитку, який характеризується багатьма змінами.
Середній етап розвитку охоплює учнів-підлітків 7-9 класів.
Підлітковий вік – це один з найважливіших етапів життя людини. У ньому багато джерел і починань всього подальшого становлення особистості. Вік цей нестабільний, ранимий, важкий і виявляється, що він більше, ніж інші періоди життя, залежить від реальностей довкілля [20, c. 238].
У цей період відбувається перебудова всього організму, відбувається статеве дозрівання. Активізація діяльності статевих та інших залоз внутрішньої секреції спричинює інтенсивний фізичний і фізіологічний розвиток.
Прискорюється ріст організму, досягаючи для хлопчиків найвищих показників у 13 років і продовжуючись до 15-17 років. У дівчаток цей процес розпочинається і закінчується на два роки раніше. Зміцнюється м’язово-скелетна система, зростає фізична сила. Помітною є невідповідність розвитку серця, маси тіла і судинної системи, що не дозволяє постачати потрібної кількості крові до різних ділянок тіла, зокрема до мозку. Вага головного мозку наближується до показників дорослої людини. Далі розвиваються специфічно людські ділянки мозку (лобні, частково скроневі і тім’яні), відбувається внутрішньоклітинне вдосконалення кори головного мозку, збагачуються асоціаційні зв’язки між різними ділянками мозку. Досконалішими стають гальмівні процеси. Інтенсивно розвивається друга сигнальна система. Все це виражається в розумовій активності підлітка, зростанні контрольної діяльності кори великих півкуль стосовно підкірки тощо [17].
Можна виділити такі характерні риси підліткового віку:
- Формування і розвиток теоретичного дискурсивного мислення (яке ґрунтується на міркуванні).
Цей віковий період особливо плідний для розвитку абстрактного (словесно-логічного) мислення. Матеріал, який засвоюють діти у школі, вимагає вищого, ніж у молодших школярів, рівня навчально-пізнавальної та мислительної діяльності, водночас він спрямований на розвиток цієї діяльності. Учні повинні оволодіти системою наукових понять математики, фізики, хімії. Саме ці предмети потребують нових способів засвоєння знань і спрямовані на розвиток теоретичного, тобто формального, рефлексивного (предметом аналізу є власна інтелектуальна операція) мислення [18, c. 217].
Новим у розвитку мислення підлітка є зміна способів розв’язування пізнавальних завдань. У підлітка розвивається вміння оперувати гіпотезами у процесі розв’язування мислительних завдань. Мислення на рівні формальних операцій передбачає вміння формулювати, перевіряти та оцінювати гіпотези, маніпулювати не тільки відомими фактами, які можна перевірити, а й думками, які суперечать наявним знанням. Це розвиває здатність підлітків планувати і передбачати.
Крім того, для даного періоду є актуальним небажання приймати все на віру, а перевірити (експериментувати).
Підлітковий вік є порою динамічного розвитку таких індивідуальних особливостей мислення, як творчість, самостійність, гнучкість.
- Розвиток логічної пам’яті.
Підлітковий вік пов’язаний з перебудовою пам’яті. Набуває активного розвитку логічна пам’ять та уповільнюється розвиток механічної (через часте використання логічної). Через велику кількість предметів та обсяг інформації, яку підліток повинен запам’ятати, активно розвивається й опосередкована пам’ять.
Саме в цей віковий період відбувається зміна залежності між пам’яттю та мисленням (пам’ять зумовлюється мисленням).
Основним завданням педагога у роботі з підлітками є цілеспрямований розвиток процесів пам’яті: запам’ятовування, збереження, відтворення, а також логічної пам’яті, що визначально впливає на розвиток їх інтелекту і здібностей [18, c. 217].
Навчання в 7-9 класах вимагає високої концентрації уваги, здатності зосереджуватись на змісті навчальної діяльності та одночасно відволікатися від сторонніх подразників, що потребує вольових зусиль. Наприклад, матеріал із математики має понятійний, узагальнений і логічно організований характер, підліток мусить виявляти неабияку інтелектуальну активність під час його первинного засвоєння (пояснення нового матеріалу вчителем). Так, для доведення теореми не достатньо просто слухати. Найменша неуважність протягом короткого часу може спричинити нерозуміння всього подальшого пояснення, оскільки засвоєння певних частин такого матеріалу можливе лише на основі розуміння та усвідомлення попередніх суджень.
На вчителя покладається велика відповідальність, щодо залучення уваги підлітків, для цього варто використовувати різні методи, залучати їх до самостійної діяльності, зацікавити новим матеріалом.
- Почуття дорослості.
Г. М. Прихожан вважає, що почуття дорослості виступає як стимул активності підлітка, спрямованої на переорієнтацію з «дитячих» норм на «дорослі», на засвоєння цінностей, норм, установок, які з точки зору підлітків підтверджують уявлення про них як про дорослих [6, c. 348].
У цей період вони негативно реагують на будь-які вимоги дорослих, яскраво виявляються ознаки емансипації. Прагнуть вільно обирати способи виконання своїх обов’язків і одночасно бояться проявити слабкість, уникають діяльності, яка може спричинити чиїсь насмішки або відчуття невпевненості у своїх силах.
Головним для них є те, щоб дорослі приймали їх на рівні, не вважали дітьми та враховували їх побажання.
- Прагнення до самопізнання.
Ставлення підлітка до себе, як до особистості відбувається в два етапи:
- Відбувається усвідомлення своєї відмінності від ровесників та утвердження своєї належності до світу дорослих. Намагається наслідувати поведінку дорослих, залежить від ровесників;
- Залежність від однолітків знижується. Намагається відстоювати свою точку зору. Характерний самоаналіз та з’являється здатність до самовиховання.
- Перехід від орієнтації на оцінку оточуючих до орієнтації на самооцінку.
Самооцінка у підлітковому віці зазвичай стосується основних моральних якостей. У цей віковий період діти не є достатньо самокритичними, їх самооцінка є нестійкою та не завжди адекватною.
- Підвищена чутливість до оцінок оточуючих, вразливість.
У зв’язку з швидкою зміною зовнішності у багатьох підлітків може виникати комплекс неповноцінності. Це може бути пов’язане з тим,що їхні параметри не відповідають тим вимогам, які вони до себе пред’являють. Саме через це думка оточуючих сприймається досить різко та болісно.
Не завжди підліток може показати своє переживання з приводу зауваження, перевівши це на жарт чи іронію. Але зазвичай це лише захисна реакція на образу. Тому потрібно досить обережно підбирати слова та жарти в адресу підлітків.
- Прагнення спілкуватися з однолітками, створювати групи.
Підлітковий період є сенситивним до розширення та збагачення стосунків з ровесниками. Це виражається у налагодженні довірливого особистісного спілкування підлітка з однолітками як провідної діяльності даного віку. Спілкування з однолітками у підлітковому періоді реалізовує функції:
- обміну інформацією, самопізнання;
- вдосконалення навичок взаємодії з однолітками;
- збагачення емпатійних навичок, здатності розділяти з іншими спільні заняття, інтереси і почуття;
- налагодження контактів з протилежною статтю і засвоєння гендерних ролей;
- становлення автономності підлітка, його незалежності від дорослих;
- здобуття досвіду набуття прийнятного соціального статусу. Саме у групі однолітків створюється нова соціальна ситуація [19, c. 156].
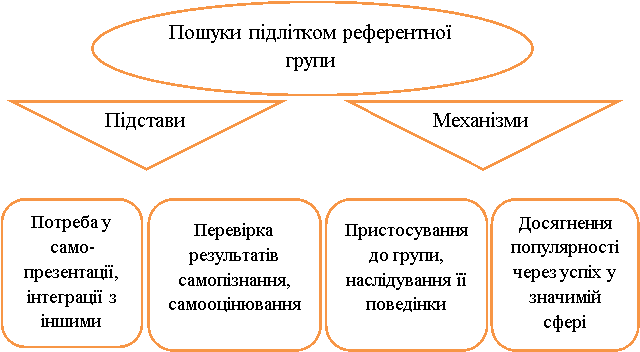 Взаємини підлітків з ровесниками виявляють нові поведінкові реакції: групування, пошуків друзів і компанії, хобі-реакції та реалізуються через налагодження дружніх взаємин і пошуки референтної групи та встановлення значимого статусу в ній (рис. 1.1.) [19, c. 157],
Взаємини підлітків з ровесниками виявляють нові поведінкові реакції: групування, пошуків друзів і компанії, хобі-реакції та реалізуються через налагодження дружніх взаємин і пошуки референтної групи та встановлення значимого статусу в ній (рис. 1.1.) [19, c. 157],
Рис. 1.1. Особливості пошуку референтної групи
- Відчуження від дорослих.
Підліток намагається своїми діями показати, що він вже дорослий, самостійний та незалежний.
Найбільш явно емоційне відчуження спостерігається в тих сім’ях, де батьки не сприймають особистість підлітка, як дорослу людину, намагаються тиснути на нього та проявляють надмірну зацікавленість їхніми особистими справами.
- Прагнення отримати визнання серед однолітків.
Тобто мати компанію друзів, де цінують, а головне – визнають успішним, гідним, просто дорослим. Така мета особлива важлива для тих, чиї батьки не визнають нових потреб свого сина чи доньки [12, c. 70].
Навчання в середніх класах школи орієнтується великою мірою на самостійне вивчення учнями навчених завдань. Підлітки люблять розв’язувати задачі проблемного характеру, які вимагають кмітливості. Їм імпонує вимога розв’язати завдання різними способами, самостійно дібрати приклади тощо. Вони з інтересом ставляться до різних практичних і лабораторних занять. Центральне місце починає займати аналіз змісту матеріалу, його своєрідності та внутрішньої політики. Тому в цьому віці спеціальним завданням для вчителя повинно стати навчання вмінню логічно обробляти матеріал. Від цього залежить не тільки успішність, глибина та міцність знань, але і можливість подальшого розвитку інтелекту та здібностей учнів. Враховуючи цю особливість, необхідно передбачати вправи, направлення на формування вмінь будувати логічно зв’язані висловлення описового, різнорідного, аргументованого характеру.
Отже, саме завдяки мистецтву вчителя, можна своєчасно розпізнати переважаючу сферу творчого напряму учня та стимулювати її розвиток. Але не треба забувати, що ті з підлітків, кому надається повна свобода, відчувають почуття тривоги, так як не знають, як цією свободою скористатись.
1.2. Поняття диференційованого навчання в педагогіці та методиці
Диференційоване навчання – це така організація навчально-виховного процесу, при якій створюються належні умови, з урахуванням типових індивідуальних особливостей учнів, за для розвитку потенційних навчальних можливостей.
Дослідженням психологічної особливості диференційованого навчання займається така галузь психології як диференціальна психологія. Вчені дослідили основні передумови необхідні за для встановлення такого навчання. Серед них можна виділити наступні:
- Починається новий етап навчання;
- Збільшується кількість навчальних предметів, шкільний матеріал стає більш складним та насиченим, позакласні та позашкільні заняття приймають інший вид та форму;
- Настає у психології «критичний вік»;
- Зростає пізнавальний інтерес;
- Розвиваються мотиви навчання, уточнюються інтереси і нахили школярів;
- Настає основний пік розвитку інтелекту, виявляються методичні здібності.
Диференціація процесу навчання передбачає позбутися від навчання всіх однаково, зменшити навантаження на учнів, створити передумови для самоствердження й самовдосконалення кожної дитини.
Основні складові технології диференційованого навчання визначаються на основі розроблених у педагогічній теорії та практиці вимог, які ставляться до педагогічної технології взагалі та до рівневої організації навчальної діяльності учнів зокрема:
- визначення чіткої системи цілей навчання;
- встановлення вихідного стану навчальних можливостей учнів, виокремлення типологічних груп;
- конструювання навчального циклу, створення програми впливів з урахуванням перехідних станів учнів кожної типологічної групи;
- реалізація запланованих завдань, організація різнорівневої навчальної діяльності школярів;
- одержання інформації про хід діяльності, оцінювання поточних результатів;
- уточнення цілей навчання, внесення необхідних корективів;
- підсумкове оцінювання результатів навчання;
- повторне відтворення циклу без змін або з корекцією.
Існують різні види диференціації. Розглянемо найбільш розповсюджені з них:
- Диференціювання за здібностями.
Учнів розподіляють по групами враховуючи їхні загальні чи індивідуальні здібності. Наочно даний поділ спостерігається під час розподілу дітей по профільним класам (фізико-математичні, гуманітарні, хіміко-біологічні, історично-правові тощо).
Дане диференціювання має й свої недоліки. Дитина, яка потрапила до класу здібних учнів, може вважати себе кращою за інших, що нерідко спричиняє відхилення від норми у вихованні. І навпаки, діти, зараховані до класу менш здібних, щодня почуватимуться неповноцінними. Крім того, здібності дитини розвиваються, і важливе значення для її розвитку мають умови, в які вона потрапляє. Якщо її оточують більш розвинені однолітки, вона отримує більше шансів для свого розвитку. До того ж здібності людини можуть виявлятися на різних вікових етапах [24, c. 345];
- Диференціювання за відсутністю здібностей.
Діти, які не встигають з певних предметів, групуються у класи, в яких ці предмети вивчають за заниженим рівнем та меншим обсягом. Даний поділ є актуальним для Франції.
Недоліком є те, що учні отримують освіту різного рівня, в результаті чого в подальшому не будуть мати рівних можливостей для її впровадження.
- Диференціювання за майбутньою професією.
Учні навчаються у школах різного профілю (музичних, художніх тощо).
- Диференціювання за інтересами учнів.
Передбачає навчання дітей у класах чи школах з поглибленим вивченням окремих предметів. У школі такі класи формуються в результаті зацікавленості значної кількості дітей певних предметів. Зазвичай, такі класи починають формуватися починаючи з восьмого року навчання. Це пояснюється тим, що учні вже отримали базові знання загальноосвітнього рівня і мають можливість оцінити, які предмети є для них більш прийнятними за для подальшого поглиблення.
- Диференціювання за талантами.
Передбачає виявлення обдарованих дітей та створення умов для їх всебічного розвитку. Для цього проводять різноманітні конкурси, олімпіади. (У Сумах створена школа-інтернат для обдарованих дітей).
Диференційоване навчання у практичній діяльності вчителя може виражатися в наступному:
- Усі учні отримують завдання однакового рівня складності, але слабшим з них надають індивідуальну допомогу під час виконання;
- Слабші учні отримують інші, посильні для них завдання;
- Першочергово дають легкі завдання, які згодом ускладнюють додатковим завданням.
Отже, диференціювати завдання можна кількістю завдань, ступенем їх складності, ступенем самостійності виконання. Складнішим і ефективнішим видом диференційованого навчання є здійснення його в умовах поділу класу на групи залежно від рівня навчальних можливостей учнів.
Але треба пам’ятати, що диференційоване навчання на уроці потребує ґрунтовної підготовки педагога, певних умінь. Він має знати індивідуальні особливості учнів, розподілити їх за групами, розмістити ці групи, підібрати консультантів. Зміст і структура заняття потребують чіткого продумування. Особливо продуманими мають бути зміст і структура уроку, в тому числі основні й додаткові запитання, час на їх виконання, система оперативного контролю. Важливо під час уроку поєднувати індивідуальну, групову і фронтальну роботу учнів із власною педагогічною діяльністю з використання дидактичних матеріалів.
1.3. Аналіз програм і підручників з алгебри для 7 – 9 класів у контексті дослідження
В основу побудови змісту та організації процесу навчання математики покладено компетентнісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності, як здатності учня застосовувати свої знання в навчальних і реальних життєвих ситуаціях, повноцінно брати участь в житті суспільства, нести відповідальність за свої дії.
Зміст математичної освіти в основній школі структурується за такими змістовими лініями: числа; вирази; рівняння і нерівності; функції; геометричні фігури; геометричні величини. Кожна з них розвивається з урахуванням завдань вивчення математики на цьому ступені шкільної освіти, в якому виокремлюються два основні етапи: 5–6 класи і 7–9 класи. Освітні завдання на першому етапі реалізуються у процесі вивчення єдиного курсу математики, на другому – двох курсів: алгебри і геометрії [16].
Зупинимося більш детально на завданнях курсу алгебри.
У навчальній програмі з математики для загальноосвітніх навчальних закладів сформульовані такі основні завдання курсу:
- Формування умінь виконання тотожних перетворень цілих і дробових виразів;
- Формування умінь розв’язування рівнянь і нерівностей та їх систем, достатніх для їх подальшого практичного застосування, в тому числі й у суміжних предметах;
- Розв’язування прикладних задач, як результат – залучення учнів до використання рівнянь і функцій як засобів математичного моделювання реальних процесів і явищ;
- Посилення ролі обґрунтувань математичних тверджень, індуктивних і дедуктивних міркувань, формування різноманітних алгоритмів, за для розвитку логічного мислення і алгоритмічної культури школярів.
На цьому етапі шкільної математичної освіти учні починають ознайомлюватися з дійсними числами. Крім того, до відомих учням числових множин додається множина ірраціональних чисел.
Основу курсу становлять перетворення раціональних та ірраціональних виразів. У 7 класі на вивчення теми «Цілі вирази» відводиться 30 годин. А у 8 класів на тему «Раціональні вирази» 24 години. На вивчення цих тем надається найбільша кількість годин. Це пов’язано з необхідністю забезпечити формування умінь школярів виконувати основні види перетворень таких виразів, що є передумовою подальшого успішного засвоєння курсу та використання математичного апарату під час вивчення інших шкільних предметів.
Також розглядається поняття степеня з цілим показником та його властивості.
Досить вагомого значення набуває змістова лінія рівнянь та нерівностей. У 7 класі на вивчення теми «Лінійні рівняння та їх системи» надається 17 годин. У 8 класі вже розв’язують раціональні та рівносильні рівняння та вивчають тему «Квадратні рівняння», на яку відведено 16 годин. У 9 класі починають вивчати тему «Нерівності» на неї відведено 14 годин. Також розглядають й квадратні нерівності.
Значне місце відводиться застосуванню рівнянь до розв’язування різноманітних задач. Важливе значення надається формуванню умінь застосовувати алгоритм розв’язування задачі за допомогою рівняння.
У 7 класі вводиться одне з фундаментальних математичних понять – поняття функції. На її вивчення відводиться 10 годин. У цьому класі розглядається лінійна функція та її графік. Інші види функцій розглядаються у зв’язку з вивченням відповідного матеріалу, що стосується решти змістових ліній курсу. Зокрема у 8 класі в темах «Раціональні вирази» та «Квадратні корені» учні ознайомлюються з функціями ![]() ,
, ![]() ,
, ![]() та їх властивостями. У 9 класі розглядається квадратична функція, на її вивчення відводиться найбільша кількість годин – 20. Вивчення її властивостей пов’язується, зокрема, з розв’язуванням квадратних нерівностей.
та їх властивостями. У 9 класі розглядається квадратична функція, на її вивчення відводиться найбільша кількість годин – 20. Вивчення її властивостей пов’язується, зокрема, з розв’язуванням квадратних нерівностей.
Таким чином, функціональна лінія пронизує весь курс алгебри основної школи і розвивається в тісному зв’язку з тотожними перетвореннями, рівняннями і нерівностями. Властивості функцій, як правило, встановлюються за їх графіками, тобто на основі наочних уявлень, і лише деякі властивості обґрунтовуються аналітично. У міру оволодіння учнями теоретичним матеріалом кількість властивостей, що підлягають вивченню, поступово збільшується. Під час вивчення функцій чільне місце відводиться формуванню умінь будувати й аналізувати графіки функцій, характеризувати за графіками функцій процеси, які вони описують, спроможності розуміти функцію як певну математичну модель реального процесу.
Дев’ятикласники також ознайомляться з основними поняттями комбінаторики, теорії ймовірностей та статистики [16].
Кожен з підручників розвиває ідеї, які закладені в навчальній програмі. Зазвичай перехід до підручників 7 – 9 класів можна здійснити, як після підручників одного й того ж автора, так і після інших підручників з математики для 5 – 6 класів, так як зміст алгебраїчного і арифметичного блоків збігаються з змістом інших підручників для 7 – 9 класів.
Ми проаналізуємо підручники для загальноосвітніх навчальних закладів таких авторів, як Мерзляк А. Г., Полонський В. Б., Якір М. С.; Істер О. С.; Бевз Г. П., Бевз В. Г..
У кожному з підручників теоретичний матеріал викладено досить цікаво та ґрунтовно, в них міститься багато фактів з історії математики, що робить його ще більш цікавим. У даних підручниках міститься багато відомостей, які наведені без доказів, але є і багато задач на доведення.
Що стосується системи завдань, то в підручнику Істер О. С. вони поділені на чотири частини за рівнем складності. У першій частині (її позначають «1») вміщені завдання усного характеру. У другій частині («2») вміщені вправи, які вимагають від учнів лише умінь розв’язувати за алгоритмом. У третій («3») – дані завдання, при рішенні яких потрібно вміння мислити і аналізувати, а в четвертій частині («4») представлені завдання переважно творчого характеру, над якими потрібно добре поміркувати. У третьому та четвертому рівні наявні завдання на доведення та дослідження.
У підручнику за редакцією Г.П. Бевза завдання поділені на два рівні. У першій частині (її позначають «А») дані вправи, які розв’язуються за алгоритмом. У другій частині («Б») вміщені вправи, за для розв’язку яких необхідно мислити та аналізувати. У даній частині наводяться завдання на дослідження.
У кожному з цих підручників забезпечена рівнева диференціація в навчанні.
Хотілося б відзначити, що в кожному, з вибраних для аналізу, підручниках формулювання вправ цікаві та різноманітні і в них простежується практична спрямованість та зв’язок з іншими науками (наприклад, фізикою, біологією і геометрією). У кінці кожного пункту наводяться вправи на повторення та нестандартні (творчі) задачі. Крім того, багато уваги приділено обчислювальній культурі учнів.
У підручниках, зміст яких повністю відповідає сучасним освітнім стандартам, враховані результати досвіду викладання математики останніх десятиліть, а також відображені сучасні методичні та педагогічні тенденції – посилено увагу до формування обчислювальної культури в її сучасному розумінні, а також до навчання логічним прийомам рішення задач.
Уключений новий для української школи матеріал – основи комбінаторики, теорії ймовірностей та статистики.
У підручнику Істера О. С. на дану тему відведений цілий розділ з однойменною назвою. У підручнику Бевза Г. П. ця тема є складовою розділу «Елементи прикладної математики». А у підручнику Мерзляка А. Г. вона відводиться після всіх розділів, у пункті, який має назву «Для тих, хто хоче знати більше».
У даних підручниках постійно використовується математична символіка.
-
Методичними особливостями кожного з наведених підручників є:
забезпечення рівневої диференціації;
- Зміст матеріалу організовано так, що відбувається неодноразове повернення до всіх принципових питань, причому на кожному наступному етапі учні піднімаються на більш високий рівень;
- Відбувається опора на наочно-образне мислення.
Отже, можна зробити висновок, що дані підручники відрізняються посиленою увагою до арифметики, до формування обчислювальної культури в її сучасному розумінні: це припущення і оцінка результатів дій, перевірка їх на правдивість. Особлива увага приділяється навчанню арифметичним і логічним прийомам розв’язування текстових завдань. Кожен пункт цих підручників містить пункти: «Для тих, кому цікаво», «Питання для повторення», «Завдання для самоперевірки».
РОЗДІЛ ІІ. РЕАЛІЗАЦІЯ ПРИНЦИПУ ДИФЕРЕНЦІЙОВАНОГО НАВЧАННЯ НА УРОКАХ АЛГЕБРИ В ОСНОВНІЙ ШКОЛІ
2.1. Використання диференційованого підходу на різних етапах вивчення матеріалу
Необхідність введення диференційованого підходу до навчальної діяльності школярів не раз висловлював у своїх працях В. О. Сухомлинський: «До кожного учня треба підійти, побачити його труднощі, кожному дати тільки для нього призначене завдання» [22, с. 52].
Диференціація передбачає врахування індивідуальних особливостей кожного учня в умовах групування дітей в межах одного класу. Кожен учень прагне досягти мети своїми зусиллями. Клас працює як одне ціле, і в той самий час кожен іде своєю стежиною. За такої форми є можливість підійти до найслабкіших, спокійно працювати з ними безпосередньо на уроці і, водночас, розвивати здібності сильних учнів. Адже ефективність уроку – це не кращі відповіді окремих учнів, а хороші знання всіх.
Диференційоване навчання можна застосовувати на різних етапах уроку.
На етапі актуалізації опорних знань використовується підготовка до вивчення нового матеріалу і робота дворівневих груп, що дозволяє систематично повторити вивчений матеріал та підготувати учнів до усвідомлення нового матеріалу.
На етапі вивчення нового матеріалу використовуються різні способи:
- багаторазове пояснення, яке допомагає кожній дитині включитись у навчальний процес, ефективно засвоювати новий матеріал;
Даний спосіб може бути реалізований наступним чином (див. Таблицю 1)
- поєднання фронтальної, парної та індивідуальної роботи, що дозволяє застосувати в процесі вивчення нового матеріалу колективну роботу, роботу в парах та індивідуальну роботу;
- вироблення правильного, свідомого застосування набутих знань в стандартних умовах.
Таблиця 1.
Багаторазове пояснення
|
|
1 етап |
2 етап |
3 етап |
4 етап |
|
1в. |
Працюють з учителем. Виконай за зразком. |
Виконай самостійно |
Творча робота |
Спільне завдання виконай самостійно |
|
2в. |
Працюють з учителем |
Виконай за зразком |
Виконай самостійно |
Виконай самостійно |
|
3в. |
Працюють з учителем |
Працюють з учителем |
Виконай за зразком |
При потребі – допомога вчителя |
На етапі закріплення вивченого матеріалу можна застосувати такі способи реалізацій диференційованого підходу:
- зменшення міри допомоги слабшим і ускладнення завдань сильнішим учням, що сприяє переходу сильних учнів до творчих завдань, а слабшим учням – навчитися працювати самостійно;
- варіативна робота над задачами, яка дає змогу навчити кожну дитину самостійно розв’язувати задачі;
- додаткові завдання до основного, які допомагають кожній дитині відшукати самостійний шлях вирішення проблеми на різних етапах розвитку;
- вільний вибір варіантів, який дає можливість кожній дитині самостійно вибрати завдання різної складності;
- складання плану подальшої роботи.
Крім того, диференційований підхід може бути застосований і на етапі виконання домашнього завдання. Вони теж диференціюються за рівнем складності і самостійності. Обсяг диференційованих домашніх завдань такий, що їх перевірка вчителем займає не більше 5 хвилин [11, с. 129]. Якщо учням пропонуються спільні домашні завдання, то при цьому диференціюється міра допомоги різним групам школярів. Так учні першої групи, які засвоїли матеріал уроку на високому рівні, самостійно виконують домашнє завдання. Учні другої групи виконують домашнє завдання з різною мірою допомоги (алгоритми, пам’ятки, опорні таблиці тощо). Учні третьої групи, які мають низький рівень навчальних досягнень, виконують завдання за зразком.
Поряд з домашніми завданнями, спільними для всіх учнів, готуються також індивідуальні завдання, які дають можливість дітям працювати не тільки відповідно до рівня своєї підготовки, а й відповідно до розвитку своїх індивідуальних здібностей. Для сильних учнів це завдання творчого характеру. Також індивідуальні домашні завдання добираються для того, щоб ліквідувати прогалини, які виникли в знаннях окремих дітей. Для них завдання готуються на спеціальних картках. Найбільш активним учням, які на уроці добре засвоюють навчальний матеріал, пропонується виконати завдання, необхідні для наступного уроку. Деяким учням, як заохочення, надається право самим визначити домашнє завдання. Завдання на вибір стимулюють роботу кожного учня. Таким чином, під час виконання диференційованих домашніх робіт від нижчого рівня до вищого розширюються і поглиблюються знання учнів, формуються загально-навчальні уміння і навички, зокрема, вміння працювати самостійно з посібниками. Водночас створюються умови для розвитку творчих здібностей сильніших школярів, а найслабші учні ефективніше засвоюють програмовий матеріал.
2.2. Методичні розробки уроків з теми «Квадратні рівняння» (алгебра, 8 клас)
Тема: Квадратні рівняння. Неповні квадратні рівняння, їх розв’язування.
Тип уроку: засвоєння нового навчального матеріалу.
Мета:
Навчальна: домогтися засвоєння учнями означення квадратного рівняння та його коефіцієнтів, неповного квадратного рівняння; виробити уміння розпізнавати неповні квадратні рівняння, визначати їх коефіцієнти, розкладати на множники, розв’язувати неповні квадратні рівняння.
Розвивальна: розвивати абстрактне мислення, логіку, вміння порівнювати, аналізувати, робити висновки; удосконалювати навички самоконтролю та взаємоконтролю.
Виховна: виховувати відповідальне ставлення до навчання, культуру математичної мови та запису.
Обладнання: Підручник [14] Мерзляк А. Г., Полонський В. Б., Якір М. С.: «Алгебра»: підручник для 8-го класу. – Х: Гімназія, 2016. – 240 с.; картки із завданням, роздатковий матеріал.
Хід уроку
І. Організаційний етап.
1. Готовність учнів до роботи на уроці.
2. Психологічний настрій
Мені приємно знову зустрітися з вами на уроці математики. Хочу побажати вам гарного настрою на всі наступні уроки сьогодні.
ІІ. Актуалізація опорних знань.
Пропоную вам гру «Закінчити речення»:
Рівність, яка містить невідомі числа, позначені буквами, називається… (рівнянням).
Невідомі числа в рівнянні називають … (змінними).
Число, яке задовольняє рівняння, називається … (коренем або розв’язком).
Знайти всі корені рівняння або показати, що їх не існує, означає … (розв’язати рівняння).
Рівняння виду ax = b, де a і b – дані числа, називається … (лінійним рівнянням).
Числа a і b у цьому рівнянні називаються … (коефіцієнтами).
Число b ще називають … (вільний член).
Чому дорівнює значення змінної у рівняннях? (всі учні виконують завдання в зошитах, а двоє учнів – на дошці):
4x = 56
![]()
![]()
![]()
x = 56 : 4
x = 16
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Винесіть за дужки спільний множник:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
А тепер, перевірте себе і своїх однокласників, обмінявшись зошитами.
ІІІ. Мотивація навчальної діяльності. Повідомлення теми, мети, завдання уроку.
Перед вами декілька рівнянь (записані на карточках, з іншого боку на яких написані букви, які стоять у дужках поряд із рівняннями). Спробуйте розподілити дані рівняння по зовнішньому вигляду на дві групи.
1) ![]() (к)
(к)
2) x – 9 = 0 (ж)
3) 2x – 3 = 0 (г)
4) ![]() (в)
(в)
5) x = 0 (ю)
6) ![]() (а)
(а)
7) 16x – 8 = 0 (и)
8) ![]() (д)
(д)
9) ![]() (р)
(р)
10) x – 10 = 0 (о)
11) ![]() (а)
(а)
12) x + 25 = 0 (п)
13) ![]() (т)
(т)
14) 5x – 1 = 0 (м)
15) ![]() (н)
(н)
16) 4x – 10 = 0 (ф)
17) ![]() (і)
(і)
У чому відмінність між рівняннями в цих групах?
Чи всі рівняння ви можете розв’язати?
Переверніть картки першої групи та з отриманих букв складіть слово.
Що отримали? (Квадратні)
Сьогодні на уроці мова піде про рівняння, ми з вами спробуємо узагальнити свої знання про ті види рівнянь, з якими ми вже знайомі та вивчити нові, а саме квадратні рівняння та неповні квадратні рівняння. Тому запишіть тему уроку: «Квадратні рівняння. Неповні квадратні рівняння, їх розв’язування».
ІV. Сприйняття й первинне усвідомлення навчального матеріалу, осмислення зв’язку і відношень між об’єктами вивчення.
- Запропонована життєва ситуація, яку потрібно розв’язати:
Ми збираємось замінити лінолеум у нашому класі. Ширина смуги цього матеріалу дорівнює 3м. Чи можна буде покласти його двома листами, якщо довжина нашого класу на 2м більша за ширину, а площа дорівнює 48м2.
Розв’язання.
Нехай х м— ширина класу, тоді його довжина становить (х+2) м. За умовою задачі площа класу дорівнює 48м2. Тому за формулою для обчислення площі маємо рівняння х(х+2)=48.
- Бесіда
– Як будемо розв’язувати це рівняння?
– Яких знань не вистачає вам для виконання рівняння?
- Пояснення матеріалу уроку:
Рівняння виду ![]() = 0, де a, b, c – числа, причому a ≠ 0, називається квадратним рівнянням; a – 1-й коефіцієнт; b – 2-й коефіцієнт; с – вільний член цього рівняння.
= 0, де a, b, c – числа, причому a ≠ 0, називається квадратним рівнянням; a – 1-й коефіцієнт; b – 2-й коефіцієнт; с – вільний член цього рівняння.
Приклади.
![]() – квадратне рівняння; a = 3, b = 2, c = – 1.
– квадратне рівняння; a = 3, b = 2, c = – 1.
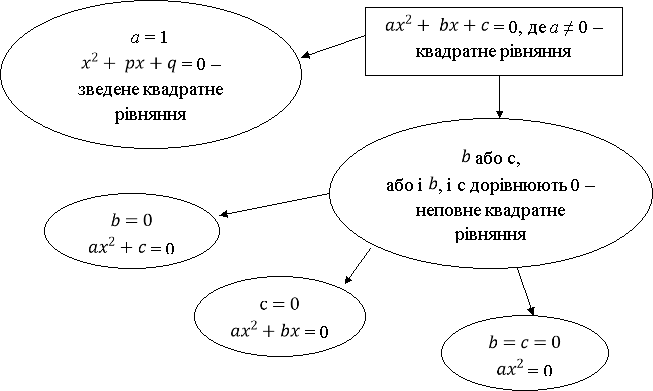
Рис. 2.1. Види квадратних рівнянь (залежно від значення коефіцієнтів)
V. Засвоєння вмінь і навичок.
1. Усні вправи (розв’язуються колективно).
- Які з наведених рівнянь є квадратними:
1) 5x – 2 = 0
4) ![]()
2) ![]()
5) ![]()
3) ![]() = 0
= 0
6) ![]()
Для квадратних рівнянь назвіть значення їх коефіцієнтів.
- Дані рівняння:
1)![]()
![]()
3)![]()
4)![]()
5) ![]()
6) ![]()
Виберіть серед них:
- зведені;
- неповні квадратні.
-
Запишіть дане рівняння у вигляді
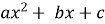 = 0:
= 0:
![]()
2)![]()
3)![]()
- Робота за вправами підручника (колективна, групова).
- Контрольно-оцінювальна робота.
№ 592
Складіть квадратне рівняння, у якому:
1) старший коефіцієнт дорівнює 6, другий коефіцієнт дорівнює 7, а вільний член дорівнює 2: ![]()
2) старший коефіцієнт дорівнює 1, другий коефіцієнт дорівнює -8, а вільний член дорівнює ![]() :
: ![]()
3) старший коефіцієнт дорівнює -0,5, другий коефіцієнт дорівнює 0, а вільний член дорівнює ![]() :
: ![]()
4) старший коефіцієнт дорівнює 7,2, другий коефіцієнт дорівнює -2, а вільний член дорівнює ![]()
![]()
№ 594
Подайте дане рівняння у вигляді ![]() , укажіть значення коефіцієнтів a, b, c:
, укажіть значення коефіцієнтів a, b, c:
1) ![]()
![]()
![]()
a = ![]()
![]()
2) ![]()
![]()
![]()
a = ![]()
![]()
3) ![]()
![]()
![]()
a = ![]()
![]()
![]()
4)![]()
![]()
![]()
a = ![]()
![]()
№ 601
Розв’яжіть рівняння:
1) ![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
![]()
3) ![]()
![]()
![]()
![]()
![]()
4) ![]()
2![]()
2![]()
![]()
![]()
![]()
5) ![]()
![]()
![]()
![]()
6)![]()
![]()
Рівняння розв’язку не має.
За окремими завданнями працюють по два учні біля дошки. Після виконання завдання міняються місцями, аналізують розв’язання і оцінюють один одного.
Методичний коментар
На даному уроці діти вивчають новий матеріал, знайомляться з квадратними рівняннями; неповними квадратними рівняннями та основними способами їх розв’язання. Тому робота на цьому етапі уроку полягає в тому, щоб розглянути найтиповіші приклади завдань, що передбачають вказання коефіцієнтів квадратного рівняння, а також розв’язання неповних квадратних рівнянь, вироблення певних стандартних підходів до їх розв’язання.
VI. Підсумки уроку. Домашнє завдання.
- Бесіда (рефлексія).
- Чи сподобалось вам працювати на сьогоднішньому уроці?
- Що б ви зробили по іншому?
- Чи зрозуміли ви способи розв’язання неповних квадратних рівнянь?
- Оцінювання учнів.
- Домашнє завдання
Опрацювати § 18, скласти свої рівняння, які ілюстрували б кожен випадок розв’язування неповних квадратних рівнянь, № 595, № 602.
№ 595
Подайте дане рівняння у вигляді ![]() , укажіть значення коефіцієнтів a, b, c:
, укажіть значення коефіцієнтів a, b, c:
![]()
![]()
![]()
![]()
a = ![]()
![]()
![]()
![]()
![]()
![]()
a = ![]()
![]()
№ 602
Розв’яжіть рівняння:
1) ![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
![]()
3) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4) ![]()
![]()
![]()
Тема: Розв’язування неповних квадратних рівнянь.
Тип уроку: закріплення навичок та умінь.
Мета:
Навчальна: закріпити знання учнів щодо означення квадратного рівняння та його коефіцієнтів, неповного квадратного рівняння, видів неповних квадратних рівнянь та способів їх розв’язування; формувати вміння визначати коефіцієнти рівняння, розкладати на множники, розв’язувати неповні квадратні рівняння.
Розвивальна: розвивати уважність, уміння порівнювати, співставляти, вміння викладати думку словесно та письмово.
Виховна: виховувати відповідальність, акуратність; культуру записів на дошці і в зошиті; свідоме ставлення до здобуття та засвоєння знань.
Обладнання: Підручник [14] Мерзляк А. Г., Полонський В. Б., Якір М. С.: «Алгебра»: підручник для 8-го класу. – Х: Гімназія, 2016. – 240 с.; мушля та перлини з картону.
Хід уроку
І. Організаційний етап.
1. Готовність учнів до роботи на уроці.
2. Психологічний настрій
На сьогоднішньому уроці ми продовжимо вдосконалювати наші знання, набуті на попередніх уроках.
ІІ. Перевірка домашнього завдання.
Проводимо фронтальне опитування.
ІІІ. Мотивація навчальної діяльності. Повідомлення теми, мети, завдання уроку.
Сьогодні на уроці попрацюємо нестандартно, відшукаємо помилки у записах наших однокласників, а головне, назбираємо повну мушлю перлин мудрості.
ІV. Актуалізація опорних знань.
Отже, проведемо урок з ученим Аль-Хорезмі.

Рис. 2.2. Портрет Аль-Хорезмі
Вчений багато читав, вивчав перську, арабську, давньогрецьку мови, керував науковими роботами у Будинку мудрості. Ввівши Аль-джебр, і Аль-мукабала, значно покращив розв’язування рівнянь.
Що означає Аль-джебр і Аль-мукабала?
Аль-джебр – перенесення членів з однієї частини рівняння в іншу.
А ви знаєте, як виконати таку дію? (Учні повторюють правила)
Аль-мукабала – почленне віднімання від обох частин рівняння однакових членів. (Учні повторюють правила)
На дошці прикріплює мушлю з картону, в яку діти на протязі уроку будуть збирати перлини мудрості.
- Кросворд
На дошці записаний кросворд:
- Рівність зі змінною. (рівняння)
- Другий степінь числа. (квадрат)
- Числовий множник алгебраїчного виразу. (коефіцієнт)
- Розв’язок рівняння. (корінь)
- Графік квадратного рівняння. (парабола)
- Бесіда за запитаннями:
- Які рівняння називають квадратними?
- Яка класифікація квадратних рівнянь?
-
Прокоментуйте види рівнянь:
-
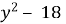 = 0;
= 0;
-
 = 0;
= 0;
-
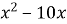 = 0.
= 0.
-
- Скільки дійсних коренів можуть мати квадратні рівняння?
- Наведіть свої приклади з домашньої роботи, які проілюструють усі випадки.
Молодці. Отже, перша перлина мудрості потрапляє в нашу мушлю.
Усний рахунок:
Розв’язати рівняння, записані на дошці:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рівняння розв’язку не має.
І, як ми бачимо, ще одна перлина мудрості потрапила до нашої мушлі.
V. Закріплення знань.
- Знайди помилку
Біля дошки працюють учні – помічники вчителя, які при розв’язуванні рівнянь зумисно допускають помилку. Учні класу повинні знайти її і виправити, аргументувавши свої дії.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3![]()
![]()
![]()
![]()
![]()
І знову перлина мудрості прямує до нашої мушлі.
А тепер розв’яжемо рівняння, які містять дробові вирази: № 608.
№ 608
1) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
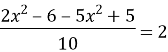
![]()
![]()
![]()
Рівняння розв’язку не має.
Чергова перлина поповнює скарб мушлі.
- Графічний спосіб розв’язування рівнянь.
Розв’язати графічно рівняння:
![]()
![]()
![]()
Ще одна перлина з’явилась у нашій колекції.
VI. Підсумки уроку. Домашнє завдання.
- Бесіда (рефлексія)
Чи виконали ви завдання, які ставили перед собою на початку уроку?
Аналізуючи проведений урок та здобуті на ньому знання, учні перераховують перлини з мушлі і пригадують, за що вони їх отримали.
- Оцінювання учнів
- Створення «ситуації успіху»
Що ж, доволі повна наша мушля. Але це далеко не всі знання, які ви отримаєте під час вивчення цієї теми. Тож нехай ваші мушлі знань завжди поповнюються все новими і новими перлинами мудрості!
- Домашнє завдання
Повторити §18, № 604 – І група., № 609 – ІІ група;
Підібрати самостійно два рівняння і розв’язати їх графічно.
№ 604
Розв’яжіть рівняння:
1) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
№ 609
Розв’яжіть рівняння:
1) ![]()
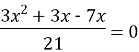
![]()
![]()
![]()
![]()
![]()
![]()
2) ) ![]()
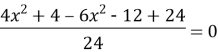
![]()
![]()
![]()
Тема: Розв’язування квадратних рівнянь.
Тип уроку: систематизації та узагальнення знань (нетрадиційний урок).
Мета:
Навчальна: узагальнити та систематизувати знання, уміння і навички учнів з теми.
Розвивальна: розвивати логічне мислення, вміння викладати думку словесно та письмово.
Виховна: виховувати самостійність, наполегливість, інтерес до предмету, культуру записів на дошці і в зошиті.
Обладнання: картки з індивідуальними завданнями, проектор.
Хід уроку
І. Організаційний етап.
«Алгебра щедра, вона часто дає більше, ніж у неї просять» – так стверджував великий математик Д’Аламбер, і наш урок буде тому підтвердженням.

Рис. 2.3. Портрет Д’Аламбера
Сьогодні у нас незвичайний урок. Щоб підбити підсумок з теми «Квадратні рівняння», проведемо з вами ділову гру під назвою «Компетенція».
Виникає питання: а що ж означає це слово?
Компетенція – це готовність учня використовувати засвоєні знання, навчальні вміння та навички, а також засоби діяльності в житті для виконання практичних та теоретичних завдань.
Компетентний (з латинської – здатний, відповідний) – це той, хто вміє застосовувати набуті знання та досвід.
Отже, наскільки ви компетентні щодо розв’язання квадратних рівнянь, і будемо з’ясовувати.
Наш клас – це три команди «конкурентів» (α, β, γ), у кожної є свій «спонсор знань», який зможе вам упродовж уроку надавати допомогу, а також буде мені допомагати фіксувати ваші успіхи. «Спонсори» – учні 9-го класу, які вже впевнились, наскільки важлива в курсі математики тема «Квадратні рівняння».
Умови нашої роботи:
ІІ. Перший етап змагань
І етап проходить під девізом «Хай живе теорія!»
Мета: актуалізація опорних знань з теоретичного матеріалу.
Один з варіантів. Для виконання домашнього завдання було запропоновано самостійно знайти цікаву та корисну інформацію з теми, яку вивчаємо. У нас є такі учні, які склали або доповідь, або реферат.
Учні роблять повідомлення про свою роботу.
Перший учень:
Необхідність розв’язувати рівняння не тільки першого, а й другого степеня ще в давнину була обумовлена потребою розв’язати задачі, пов’язані із знаходженням площ земельних ділянок, із земляними роботами військового характеру, з розвитком астрономії і самої математики. Квадратні рівняння уміти розв’язувати близько 2000 років до н.е. вавилоняни. Застосовуючи сучасну алгебраїчну символіку, можна сказати, що в їх клинописних текстах трапляються такі квадратні рівняння: ![]() ;
; ![]() .
.
Хоча рівень розвитку алгебри у Вавилоні був високим, проте у клинописних текстах поняття від’ємного числа, а також загальні методи розв’язування квадратних рівнянь відсутні.
Другий учень
Квадратні рівняння цікавили й Діофанта. Попри те, що в «Арифметиці» Діофанта немає систематичного викладу алгебри, у ній міститься систематизований ряд задач, що розв’язуються за допомогою складання квадратних рівнянь. Наприклад, рівняння з «Арифметики» Діофанта: ![]() ;
; ![]() .
.
Задачі на квадратні рівняння зустрічаються вже в астрономічному тракті «Аріабхаттіам», складеному в 499 р. індійським математиком і астрономом Аріабхаттою. Інший індійський учений, Бахмагупта (VI ст.), виклав загальне правило розв’язування квадратних рівнянь, зведених до єдиної канонічної форми: ах2+bx = c, а>0. Правило Брахмагупти по суті збігається з нашим.
Третій учень
В алгебраїчному трактаті ал-Хорезмі дається класифікація лінійних і квадратних рівнянь. Автор нараховує 6 видів рівнянь:
- Квадрати, що дорівнюють кореням, тощо ах 2 = bx.
- Квадрати, що дорівнюють числу, тобто ах2 = с.
- Корені, що дорівнюють числу, тобто ах = с.
- Квадратні числа, що дорівнюють кореням, тобто ах2+с = bx.
- Квадрати і корені, що дорівнюють числу, тобто ах2+bx = с.
- Корені і числа, що дорівнюють квадратам, тобто bx + с = ах2
Трактат ал-Хорезмі є першою книжкою, що дійшла до нас, в якій систематично викладено класифікацію квадратних рівнянь і подано формули їх розв’язування.
Четвертий учень
Формули розв’язування квадратних рівнянь в Європі були вперше викладені у «Книзі абака» італійського математика Леонардо Фібоначчі в 1202 р. Загальне правило розв’язування квадратних рівнянь виду х2+bx = с при всіх можливих комбінаціях знаків коефіцієнтів b і с було сформульовано в Європі лише у 1544 р. М.Штизелем. Розв’язуванням квадратних рівнянь займалися Вієт, Тарталья, ар дано, Бомбеллі. Лише в Х VIІ ст. завдяки роботам Жирара, Декарта, Ньютона та інших учених спосіб розв’язування квадратних рівнянь набуває сучасного виду.

Рис. 2.4. Портрет Леонардо Фібоначчі
«Спонсори» фіксують активність на цьому етапі.
ІІІ. Другий етап змагань
Цікавинки навчання.
«Перевір себе». На цьому етапі уроку вам необхідно розв’язати математичний кросворд. Для виконання цього завдання ви вдома повинні були знайти відповіді на деякі запитання, які ми ще не вивчали.
Умови. «Спонсор» видає кросворди кожному учню, який підписує ім’я (заповнює олівцем).
1. Рівняння виду ![]() (квадратне)
(квадратне)
2. Сума трьох доданків стандартного вигляду (тричлен)
3. Рівняння з однією змінною, які мають одні й ті ж корені. (рівносильне)
4. Числа ![]()
5. Значення змінної, при якому рівняння обертається в вірну числову рівність. (корінь)
6. Стародавній грецький математик, який винайшов способи розв’язування квадратних рівнянь без звернення до геометрії. (Деофант)
7. Невід’ємне значення квадратного кореня. (арифметичний)
8. Рівність, яка містить невідоме. (рівняння)
9. Квадратне рівняння, в якому хоча б один з коефіцієнтів ![]()
10. Стародавнє місто-батьківщина математики як науки. (Вавилон)
11. Коефіцієнт із квадратного рівняння, що показує доданок без змінної. (вільний)
12. Французький математик, який вивів формули, які виражають залежність коренів рівняння від його коефіцієнтів. (Вієт)
Якщо кросворд розгадано вірно, то у виділеному вертикальному стовпчику можна прочитати термін, що відноситься до теми (дискримінант).
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
|
|
|
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
|
|
|
|
|
|
|
|
|
|
|
|
Підсумок. Звіряємо відповіді, «спонсори» перевіряють, оголошують кількість правильних відповідей, заносять до таблиці результати кожного учня за урок.
Висновок. З’ясували всі теоретичні питання, готові до наступного етапу.
Якщо кросворд розгадано вірно, то у виділеному вертикальному стовпчику можна прочитати термін, що відноситься до теми (дискримінант).
ІV. Третій етап змагань
«Практика – велика справа»
Мета: контроль якості засвоєння знань.
Колективна робота в групах «Лови помилку».
Умови. Дані тести обговорюємо в команді, усне розв’язування.
Після кожного завдання – відповідь.
Індивідуальні практичні завдання
Кожен учень має право вибирати один з 3-х запропонованих варіантів.
Оцінювання:
І рівень – 2 б.
ІІ рівень – 3 б.
ІІІ рівень – 4 б.
У цей час учні працюють біля дошки.
Тест. Квадратні рівняння
Варіант 1
- Яке з рівнянь не має розв’язків?
а) х2+144х = 0; б) х2 – 14 = 0;
в) х2+14 = 0; г) х2 = 40.
- Скільки коренів має рівняння х2+6х+9 = 0?
а) один; б) два;
в) жодного; г) безліч.
- Корені квадратного рівняння 2х2 + 3х - 2 = 0 обчислюється за виразом.
- Сума коренів квадратного рівняння х2 – 4х +3 = 0 дорівнює:
а) 3; б) 4; в) – 3; г) – 4.
Завдання практичного характеру
Розв’язати рівняння.
І рівень
1) х2 – 6х = 0; 2) х2 = 81;
3) 3х2 -7 х +4= 0; 4) х2 – 4х + 3= 0.
ІІ рівень
1) х2 – 14х +48 = 0; 2) 5х2 +20 = 0;
3) 6х2 -12 х = 0; 4) 6х2 – 5х + 1 = 0
ІІІ рівень
- (7+2y)(7-2y) + 6y2 = 49+7y.
- (x2 – 0,64) (x2– 4x – 12) = 0.
-
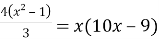
Завдання для учнів біля дошки
1 учень. Теорема Вієта.
1) За даними числа 3; 0,5 скласти квадратне рівняння.
2) х2 – х -56 = 0;
2 учень. Розв’язати неповне квадратне рівняння.
1) 3х2 – 27 = 0; 2) 6х2 = 42х;
3) 0,1х2 = 0; 4) ![]() = 3.
= 3.
3 учень.
1) ![]() =
= ![]()
2) (х-2)2 +48 = (2 – 3х)2.
V. Підсумки урока. Домашнє завдання.
- «Спонсори» підбивають підсумок за всіма видами робіт.
- А тепер проаналізуйте рівень своїх вмінь та вискажіть їх, використовуючи тільки дієслова «знаю» та «вмію».
- Спробуємо проаналізувати свій емоційний настрій на уроці.
Чи було вам було комфортно на цьому уроці? Використайте емблеми і віддайте «спонсору».
- радість успіху,
- отримав деяку суму знань,
- незадоволений собою на деяких етапах уроку.
«Спонсори» підбивають підсумок – кількість балів.
Учитель. На початку уроку клас був поділений на три команди «конкурентів», але наш урок стверджує протилежне, що ви – клас однодумців, які вміють застосовувати набуті знання, а це означає, що кожний з вас як і сьогодні, так і в майбутньому буде компетентний у певній галузі. Дякую за співпрацю на уроці.
Домашнє завдання.
Повторити теоретичний матеріал: означення, формул коренів квадратного рівняння. Розв’язати рівняння:
1) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
Рівняння розв’язку не має.
Висновки
Питання диференційованого навчання на сучасному етапі розвитку школи є найбільш актуальним та доцільним. Головна мета диференціації – це забезпечити базовий рівень знань кожному учневі, а здібним учням – надати можливість глибше опанувати предмет. Тобто, прикладний рівень – для всіх учнів, творчий – для здібних.
- Ми охарактеризували особливості учнів 7 – 9 класів. Вони охоплюють підлітковий період. А нам всім відомо, що підлітковий вік – це період статевого дозрівання. Цими процесами обумовлюється багато феноменів різних проявів підлітка. Зокрема, спостерігаються підвищена збудливість нервової системи, нестійкість і суперечливість емоцій, підвищена тривожність, пов’язана зі спілкуванням з однолітками. Підлітковий вік – сприятливий період для формування й розвитку «практичного інтелекту», атрибутами якого прийнято вважати здоровий глузд, кмітливість, інтуїцію та «золоті руки». Саме в підлітковому віці під впливом навчально-виховної роботи школи й позашкільних установ, під впливом вивчення основ наук починають формуватися і яскраво проявлятися здатності підлітків до тих або інших видів діяльності. Це пояснюється тим, що саме в підлітковому віці виникають глибокі, діючі, стійкі інтереси, формується свідоме, активне відношення до навколишньої реальності, розвивається творче мислення. У зв’язку з початком серйозного й систематичного навчання математиці формуються математичні знання. На основі вивчення математики й фізики дуже помітним є формування в підлітків конструктивно-технічних здібностей. Для успішної співпраці з учнями підліткового віку необхідно знати психологічні особливості дітей, оскільки саме це дозволить успішно вибрати правильні методи й прийоми викладання.
2. Ми визначили сутність поняття диференційованого навчання в педагогіці та методиці. Диференційоване навчання – це така організація навчально-виховного процесу, при якій створюються належні умови, з урахуванням типових індивідуальних особливостей учнів, за для розвитку потенційних навчальних можливостей.
Диференціація процесу навчання передбачає позбутися від навчання всіх однаково, зменшити навантаження на учнів, створити передумови для самоствердження й самовдосконалення кожної дитини.
Основні складові технології диференційованого навчання визначаються на основі розроблених у педагогічній теорії та практиці вимог, які ставляться до педагогічної технології взагалі та до рівневої організації навчальної діяльності учнів зокрема.
Крім того, ми розглянули та навели коротку характеристику основних видів диференціації, таких як: диференціювання за здібностями, за відсутністю здібностей, за майбутньою професією, за інтересами учнів, за талантами.
Але треба пам’ятати, що диференційоване навчання на уроці потребує не тільки знань та зацікавленості з боку учнів, а й ґрунтовної підготовки педагога, його певних умінь.
3. Ми провели аналіз програм та підручників з алгебри для 7-9 класів.
За основу нашого аналізу ми взяли навчальну програму з алгебри для загальноосвітніх навчальних закладів. З’ясували, що основу курсу становлять перетворення раціональних та ірраціональних виразів.
Крім того, встановили, що функціональна лінія пронизує весь курс алгебри основної школи і розвивається в тісному зв’язку з тотожними перетвореннями, рівняннями і нерівностями. У міру оволодіння учнями теоретичним матеріалом кількість властивостей, що підлягають вивченню, поступово збільшується. Під час вивчення функцій чільне місце відводиться формуванню умінь будувати й аналізувати графіки функцій, характеризувати за графіками функцій процеси, які вони описують, спроможності розуміти функцію як певну математичну модель реального процесу.
Також, ми проаналізували підручники для загальноосвітніх навчальних закладів таких авторів, як Мерзляк А. Г., Полонський В. Б., Якір М. С.; Істер О. С.; Бевз Г. П., Бевз В. Г..
З’ясували, в чому їх схожість, а в чому відмінність. У кожному з підручників теоретичний матеріал викладено досить цікаво та грунтовно, в них міститься багато фактів з історії математики, що робить його ще більш цікавим.
Особлива увага приділяється навчанню арифметичним і логічним прийомам розв’язання текстових завдань. Кожен пункт цих підручників містить пункти в яких наявні задачі творчого характеру, за для поглиблення та зацікавлення учнів.
4. Ми розглянули основні способи використання диференційованого навчання на різних етапах уроку. Описали, які способи доцільно застосовувати на кожному з етапів уроку. Навели приклади.
5. У курсовій роботі ми навели приклади конспектів уроків з теми «Квадратні рівняння». Ми склали три конспекти на різну тему та різного типу. Перший план-конспект уроку засвоєння нового навчального матеріалу на тему: «Квадратні рівняння. Неповні квадратні рівняння, їх розв’язування». Другий – закріплення умінь та навичок на тему: «Розв’язування неповних квадратних рівнянь». Та останній – нетрадиційний урок (узагальнення й систематизації) з теми: «Розв’язування квадратних рівнянь».
Отже, ми можемо з впевненістю стверджувати, що на сьогоднішній день продуктивне навчання школярів не можливе без використання диференційованого підходу.
Список використаних джерел
- Бабенко С. П. Алгебра. 8 клас: Розробки уроків. / С. П. Бабенко. – Х.: Ранок, 2008. – 304 с.
- Бевз Г. П. Алгебра: підруч. для 7 класу згальноосвіт. навч. закладів / Г. П. Бевз, В. Г. Бевз. – К.: Зодіак-ЕКО, 2007. – 304 с.
- Бевз Г. П. Алгебра: підруч. для 8 класу згальноосвіт. навч. закладів / Г. П. Бевз, В. Г. Бевз. – К.: Зодіак-ЕКО, 2008. – 256 с.
- Бевз Г. П. Алгебра: підруч. для 9 класу згальноосвіт. навч. закладів / Г. П. Бевз, В. Г. Бевз. – К.: Зодіак-ЕКО, 2009. – 288 с.
- Гамезо М.В. Возрастная и педагогическая психология: Учеб. пособие для студентов всех специальностей педагогических вузов / М.В. Гамезо, Е.А. Петрова, Л.М. Орлова – М. : Педагогическое общество России, 2003. – 512 с.
- Дубровина И. В. Практическая психология образования: Учебное пособие 4-е изд. / И. В. Дубровина – СПб.: Питер, 2004. – 592 с.
- Істер О. С. Алгебра: підруч. для 7 класу згальноосвіт. навч. закладів / О. С. Істер. – К.: Генеза, 2015. – 256 с.
- Істер О. С. Алгебра: підруч. для 8 класу згальноосвіт. навч. закладів / О. С. Істер. – К.: Генеза, 2016. – 272 с.
- Істер О. С. Алгебра: підруч. для 9 класу згальноосвіт. навч. закладів / О. С. Істер. – К.: Генеза, 2017. – 264 с.
- Колягин Ю.М. Методика преподавания математики в средней школе. Общая методика: Учеб. пособие для студентов физ.-мат. факультетов пед. Вузов / Ю.М. Колягин, В.А. Оганесян, В.Я. Саннинский, Г.Л. Луканкин – М.: Просвещение, 1975. – 462 с.
- Косякевич О. В. Технологія диференціального навчання молодших школярів/ О. В. Косякевич // Вісник Житомирського державного університету. – 2008. – № 44. – С. 127–130.
- Лєскова А. А. Психологічні особливості молодшого підліткового віку / А. А. Лєскова // Теоретичні та практичні засади діяльності класного керівника 7-го класу. Науково-методична збірка. – 2014. – С. 68–76.
- Мерзляк А. Г. Алгебра: підруч. для 7 класу згальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2015. – 256 с.
- Мерзляк А. Г. Алгебра: підруч. для 8 класу згальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2016. – 240 с.
- Мерзляк А. Г. Алгебра: підруч. для 9 класу згальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2017. – 272 с.
- Навчальна програма для 5 – 9 класів з математики 2017 року [Електронний ресурс]. – Режим доступу: http://mon.gov.ua/activity/education/zagalna-serednya/navchalni-programy.html
- Психологічні особливості підліткового віку [Електронний ресурс]. – Режим доступу: http://5fan.ru/wievjob.php?id=7297
- Савчин М. В. Вікова психологія: Навч. посіб. / М. В. Савчин, Л. П. Василенко – К.: Академвидав, 2005, – 300 с.
- Сергєєнкова О. П. Вікова психологія: Навч. посіб. / О. П. Сергєєнкова, О. А. Столярчук, О. П. Коханова, О. В. Пасєка – К.: Центр учбової літератури, 2012, – 376 с.
- Скрипченко О. В. Вікова та педагогічна психологія: Навч. посіб. / О. В. Скрипченко, Л. В. Долинська, З. В. Огороднійчук та ін. – К.: Просвіта, 2001. – 416 с.
- Слєпкань З. І. Методика навчання математики: Підручник / З. І. Слєпкань. – К. : Вища шк., 2006. – 582 с.
- Сухoмлинський В. O. Вибранi твoри : в 5 т. / В. О. Сухoмлинський – К.: Рад. шкoла, 1977. – Т. 3. – 612 с.
- Унт И. Э. Индивидуализация и дифференциация обучения. – М.: Педагогика, 1990. – 192 с.
- Фіцула М. М. Педагогіка: Навчальний посібник для студентів вищих педагогічних закладів освіти / М. М. Фіцула – К.: Академія, 2002, – 528 с.
- Чашечникова О. С. Впровадження рівневої диференціації навчання математики через застосування завдань на дослідження / О. С. Чашечникова, З. Б. Чухрай // Нова педагогічна думка. – Рівне, 2008. – № 3. – С. 75–78.
- Чашечникова О. С. Теоретико – методичні основи формування і розвитку творчого мислення учнів в умовах диференційованого навчання математики: дис. … д-ра пед.. наук: спеціальність: 13.00.02 – теорія та методика навчання (математика) / О. С. Чашечникова. – СумДПУ ім. А. С. Макаренка. – Суми, 2011. – 558 с.
- Черкасов Р. С. Методика преподавания математики в средней школе: Учебн. пособ. / Р. С. Черкасов, А. А. Столяр – М. : Просвещение, 1985. – 336 с.

про публікацію авторської розробки
Додати розробку
