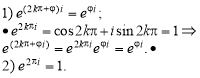ПАКЕТ НАВЧАЛЬНО-МЕТОДИЧНОГО ЗАБЕЗПЕЧЕННЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА»
ПАКЕТ НАВЧАЛЬНО-МЕТОДИЧНОГО ЗАБЕЗПЕЧЕННЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА»
1.Властивості та графіки тригонометричних функцій. Властивості та графіки обернених тригонометричних функцій.
2.Поняття комплексного числа. Основні співвідношення. Алгебраїчна форма комплексного числа. Дії над комплексними числами, заданими в алгебраїчній формі. Геометрична інтерпретація комплексних чисел. Полярні координати точки на площині. Тригонометрична форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до тригонометричної. Показникова форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до показникової. Дії над комплексними числами, заданими в тригонометричній та показниковій формі.
ПАКЕТ
НАВЧАЛЬНО-МЕТОДИЧНОГО ЗАБЕЗПЕЧЕННЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ З ДИСЦИПЛІНИ
«ВИЩА МАТЕМАТИКА»
для студентів спеціальності
5.03060101 «Організація виробництва»
Список тем для самостійного опрацювання
- Властивості та графіки тригонометричних функцій. Властивості та графіки обернених тригонометричних функцій.
- Поняття комплексного числа. Основні співвідношення. Алгебраїчна форма комплексного числа. Дії над комплексними числами, заданими в алгебраїчній формі. Геометрична інтерпретація комплексних чисел. Полярні координати точки на площині. Тригонометрична форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до тригонометричної. Показникова форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до показникової. Дії над комплексними числами, заданими в тригонометричній та показниковій формі.
- Визначники другого і третього порядків та їх властивості. Мінор та алгебраїчне доповнення. Методи обчислення визначників. Матриці. Дії над матрицями. Обернена матриця.
- Системи лінійних рівнянь з двома і трьома змінними. Критерії сумісності системи лінійних рівнянь – теорема Кронекера-Капеллі. Основні методи розв’язування систем лінійних рівнянь: метод Гауса, за формулами Крамера, матричним способом. Прикладні задачі курсів спецдисциплін, які приводять до системи лінійних рівнянь, та їх розв’язання.
- Поняття вектора. Дії над векторами. Векторні простори. Проекція вектора на вісь. Базис на площині і в просторі. Поділ відрізка в даному відношенні. Розкладання вектора за базисом.
- Скалярний добуток векторів. Кут між векторами. Напрямні косинуси. Умови колінеарності і компланарності векторів. Векторний і мішаний добуток векторів.
- Пряма лінія в просторі. Різні види рівнянь прямої в просторі. Кут між двома прямими в просторі. Кут між прямою і площиною. Умова перпендикулярності і паралельності прямої і площини. Поняття про лінії другого порядку на площині. Загальне рівняння лінії другого порядку на площині. Коло. Еліпс. Гіпербола. Парабола. Застосування властивостей кривих другого порядку до розв’язування прикладних задач, зокрема задач економічного змісту.
- Системи лінійних нерівностей. Основні задачі і поняття лінійного програмування.
- Означення диференціалу функції. Геометричний та фізичний зміст диференціалу. Правила знаходження диференціалу. Диференціал складеної функції. Застосування диференціалу до наближених обчислень.
- Зростання та спадання функцій. Стаціонарні та критичні точки. Друга похідна та її фізичний зміст. Опуклість, точки перегину графіка функції. Асимптоти графіка функції. Загальна схема дослідження та побудова графіка функції. Найбільше та найменше значення функції на відрізку. Розв’язування прикладних задач на максимум та мінімум.
- Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. необхідна умова існування точок екстремуму. Повний диференціал. Частинні похідні вищих порядків. Похідна за напрямом. Градієнт. Умовний екстремум. Метод множників Лагранжа.
- Означення визначеного інтеграла. Інтегральні суми. Методи підстановки та інтегрування за частинами у визначеному інтегралі. Площі плоских фігур та об’єми геометричних тіл. Застосування визначених інтегралів до обчислення площ, об’ємів, шляху. Поняття про подвійний інтеграл. Зведення подвійного інтегралу до повторного.
- Основні поняття та означення. Диференціальні рівняння першого порядку. Задача Коші. Теорема про існування і єдність розв’язків. Задачі, що зводяться до диференціальних рівнянь. Диференціальні рівняння з відокремленими змінними. Лінійні та однорідні рівняння першого порядку. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами. Загальний та частинний розв’язок.
- Основні поняття та означення. Числові ряди. Збіжність рядів. Властивості збіжних рядів. Гармонійний ряд. Необхідна умова збіжності рядів. Достатні умови збіжності рядів з додатними членами: ознака порівняння, ознака д’Аламбера, ознака Коші. Знакозмінні ряди. Абсолютна та умовна збіжність. Степеневі ряди. Теорема Абеля. Область збіжності степеневого ряду. Розклад функції в ряд Тейлора та Маклорена.
Самостійне вивчення №1
Тема: Властивості та графіки тригонометричних функцій. Властивості та графіки обернених тригонометричних функцій.
Література: Д-1 с. 252-271, 312-322.
В результаті самостійного опрацювання студент повинен
знати:
-
властивості тригонометричних функцій
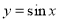 ,
, 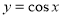 ,
, 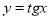 ,
, 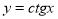 .
.
-
властивості обернених тригонометричних функцій
 ,
, 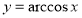 ,
, 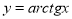 ,
, 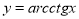 .
.
вміти:
-
будувати графіки тригонометричних функцій
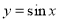 ,
, 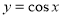 ,
, 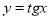 ,
, 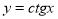 .
.
-
будувати графіки обернених тригонометричних функцій
 ,
, 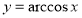 ,
, 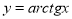 ,
, 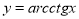 .
.
Короткі теоретичні відомості та методичні вказівки
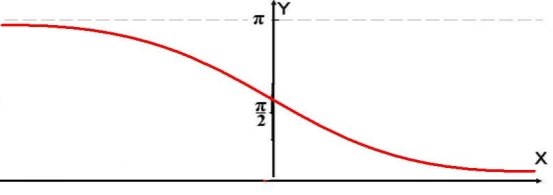
Графік функції ![]() .
.

Графік функції y=sin x називається синусоїдою.
Властивості функції y=sin х
1. Область визначення – проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція непарна, періодична з періодом Т=2π.
4. Функція зростає при - π/2+2πn<х< π/2+2πn, n є Z.
5. Функція спадає при π/2+2πn<х<3π/2+2πn, n є Z.
6. Функція має максимум у точках (π/2+2πn;0), мінімум у точках
(-π/2+2 πn;0), n є Z.
Графік функції ![]()

Графік функції ![]() називається косинусоїдою.
називається косинусоїдою.
Властивості функції ![]()
1. Область визначення – проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція парна, періодична з періодом Т=2π.
4. Функція зростає при -+2πn<х<2πn, n є Z.
5. Функція спадає при 2πn <х< π+2πn, n є Z.
6. Функція має максимум у точках (2πn;0), мінімум у точках (πn+2πn;0), n є Z.
Графік функції ![]()
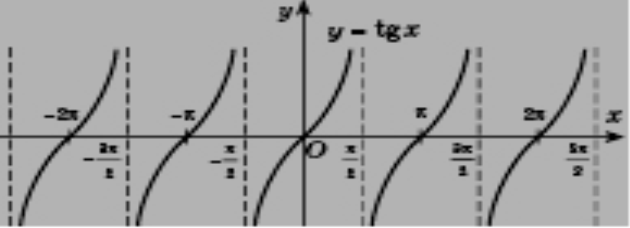
Графік функції y=tg х називається тангенсоїдою.
Властивості функції y=tg х
1. Область визначення – всі дійсні числа, крім точок x=π/2+2πn, n є Z.
2. Область значень – проміжок (-∞;+∞).
3. Функція непарна, періодична з періодом Т= π.
4. Нулі функції – точки (πn;0), n є Z.
5. Функція зростає на кожному з інтервалів ![]()
6. Функція не має екстремумів.
Графік функції ![]()
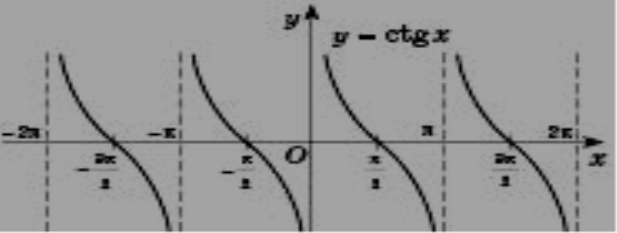
Графік функції ![]() називається котангенсоїдою.
називається котангенсоїдою.
Властивості функції y=сtg х
1. Область визначення – всі дійсні числа, крім точок x=2πn, n є Z.
2. Область значень – проміжок (-∞;+∞).
3. Функція непарна, періодична з періодом Т=π.
4. Нулі функції – точки (π/2+ πn;0), n є Z.
5. Функція спадає на кожному з проміжків ![]() .
.
6. Функція не має екстремумів.
Графік функції ![]() . Графік функції
. Графік функції ![]() .
.
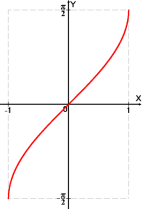
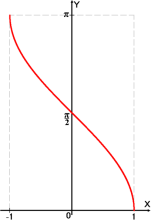
Графік функції ![]() .
.
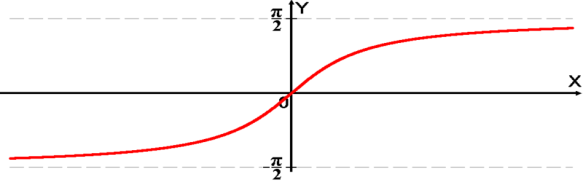
Графік функції ![]() .
.
Самостійне вивчення №2
Тема: Поняття комплексного числа. Основні співвідношення. Алгебраїчна форма комплексного числа. Дії над комплексними числами, заданими в алгебраїчній формі. Геометрична інтерпретація комплексних чисел. Полярні координати точки на площині. Тригонометрична форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до тригонометричної. Показникова форма комплексного числа. Перехід від алгебраїчної форми комплексного числа до показникової. Дії над комплексними числами, заданими в тригонометричній та показниковій формі.
Література: О-1 с.31-40; О-4 с. 29-39; О-5 с. 107-122; Д-5 с. 49-81
В результаті самостійного опрацювання студент повинен
знати:
- степені уявної одиниці;
- алгебраїчну, тригонометричну та показникову форми запису комплексного числа;
вміти:
- перетворювати комплексне число з однієї форми в іншу;
- зображувати комплексне число на координатній площині;
- виконувати дії над комплексними числами в алгебраїчній, тригонометричній, показниковій формах;
Короткі теоретичні відомості та методичні вказівки
Комплексні числа
Означення. Комплексним числом називається число виду a + іb, де a, b R, ![]() .
.
Дійсне число а називається дійсною частиною комплексного числа а + іb, а дійсне число b — його уявною частиною. Число і називається уявною одиницею.
Означення. Два комплексні числа а + bі і с + dі називаються рівними, якщо а = с і b = d.
Означення. Два комплексні числа виду а + bі та а – bі називаються спряженими.
Комплексні числа зображають на числовій площині. Для цього вибирають на площині прямокутну систему координат (рис. 1.11). Комплексне число а + іb зображається точкою M (х, y), абсциса x якої дорівнює дійсній частині комплексного числа а(х = а), а ордината у дорівнює уявній частині
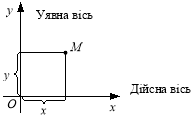
![]() Зобразити на площині комплексні числа:
Зобразити на площині комплексні числа:
3 + 4і; – 2 + 3і; – 3 – 2і; 4 + 0і; 0 + 2і.

Рис. 1.12
Дії з комплексними числами
Означення. Сумою двох комплексних чисел а + bi і с + dі називається комплексне число (а + с) + (b + d)і:
|
а + bі + (c + dі) = a + c + (b + d)і. |
![]()
1) (– 3 + 5і) + (4 – 8і) = (– 3 + 4) + (5 – 8)і = 1 + (– 3)і;
2) (– 2 + 3і) + (– 2 – 3і) = (– 2 – 2) + (3 – 3)і = – 4 + 0і = – 4.
Означення. Різницею двох комплексних чисел а + bі та с + dі називається комплексне число (а – с) + (b – d)і.
|
|
1) (– 5 + 2і) – (3 – 5і) = (– 5 – 3) + (2 – (– 5))і = – 8 + 7і.
2) (3 – 4і) – (3 + 4і) = (3 – 3) + (– 4 – 4)і = 0 + (– 8)і = – 8і.
Означення. Добутком двох комплексних чисел а + bі і с + dі називається комплексне число (ас – bd) + (аd + bс)і.
(a + bі)(c + dі) = ac + adі + bidі + bcі = ac – bd + (ad + bc)і
Зау![]() важення. На практиці не завжди користуються формулою. Можна комплексні числа множити, як двочлени.
важення. На практиці не завжди користуються формулою. Можна комплексні числа множити, як двочлени.
![]()
1) (1 – 2і)(3 + 2і) = 3 – 6і + 2і – 4і2 = 7 – 4і;
2) (а + іb)(а – іb) = а2 + b2.
Означення. Часткою двох комплексних чисел а + bі і с + dі називається комплексне число
![]() .
.
![]()
![]()
![]()
![]()
![]()
Модуль та аргумент комплексного числа
Означення. Модулем комплексного числа а + bі називається вираз ![]() який позначається r або |а + bі|.
який позначається r або |а + bі|.
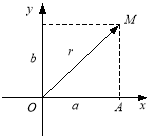
Рис. 1.13
![]()
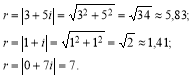
Означення. Кут між віссю Ох і відрізком ОМ, де точка М зображає комплексне число а + bі, називається аргументом комплексного числа а + bі (рис. 1.13).
Кожне відмінне від нуля комплексне число має нескінченну кількість аргументів, які відрізняються один від одного на 2k. Для числа 0 аргумент не визначений.
![]() Аргумент комплексного числа а + bі визначається формулами:
Аргумент комплексного числа а + bі визначається формулами:
![]() (1)
(1)
![]() Зауваження. Щоб користуватися цими формулами, потрібно враховувати знаки абсциси та ординати комплексного числа.
Зауваження. Щоб користуватися цими формулами, потрібно враховувати знаки абсциси та ординати комплексного числа.
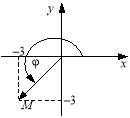
![]() Знайти аргумент комплексного числа – 3 – 3і.
Знайти аргумент комплексного числа – 3 – 3і.
За формулою (1) маємо
|
Але кут 45 не є аргументом числа Правильною є така відповідь: 225; – 135; 585 і т. д. Цей результат дістаємо, враховуючи, що абсциса та ордината комплексного числа є від’ємними, тобто точка М належить чверті ІІІ. |
Рис. 1.14 |
Означення. Значення аргументу, яке належить проміжку
(– ; ), називається головним.
![]() Для комплексних чисел – 3 – 3і; 2і; – 5і головне значення аргументу дорівнює – 135; 90; – 90.
Для комплексних чисел – 3 – 3і; 2і; – 5і головне значення аргументу дорівнює – 135; 90; – 90.
![]() Зауваження. Аргумент дійсного додатного числа має головне значення 0; від’ємного числа 180. Головні значення аргументу спряжених комплексних чисел мають одну й ту саму абсолютну величину, але протилежні знаки. Наприклад, головні значення аргументу спряжених чисел – 3 + 3і та – 3 – 3і дорівнюють 135 і – 135.
Зауваження. Аргумент дійсного додатного числа має головне значення 0; від’ємного числа 180. Головні значення аргументу спряжених комплексних чисел мають одну й ту саму абсолютну величину, але протилежні знаки. Наприклад, головні значення аргументу спряжених чисел – 3 + 3і та – 3 – 3і дорівнюють 135 і – 135.
Тригонометрична форма комплексного числа
Розглянемо трикутник ОАМ (рис. 1.13) і запишемо такі співвідношення між його сторонами:
![]() ;
; ![]() .
.
Звідси ![]() , тобто маємо:
, тобто маємо:
|
|
(2) |
Подання комплексного числа у вигляді (2) називається тригонометричною формою комплексного числа.
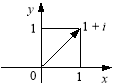
![]() Записати комплексне число 1 + і у тригонометричній формі (рис. 1.15).
Записати комплексне число 1 + і у тригонометричній формі (рис. 1.15).
Згідно з (2) маємо:
|
Рис. 1.15 |
Отже, |
Додавання і віднімання комплексних чисел простіше і зручніше виконувати, коли вони задані в алгебраїчній формі. Для інших алгебраїчних дій зручніша тригонометрична форма.
Наприклад, добуток двох чисел ![]() і
і ![]() подається так:
подається так:
![]() .
.
Піднесення комплексного числа до степеня
Степенем р комплексного числа ![]() є число
є число ![]() , де р — будь-яке ціле число. Ця формула легко виводиться за означенням добутку комплексних чисел.
, де р — будь-яке ціле число. Ця формула легко виводиться за означенням добутку комплексних чисел.
![]() Знайти
Знайти ![]() , якщо
, якщо ![]() .
.
![]() .
.
1. Якщо р = n (n — ціле число) і r = 1, дістаємо формулу Муавра:
|
|
(3) |
Якщо р — ірраціональне, то р-й степінь будь-якого числа має нескінченну множину значень.
![]() Подати sin3 та cos3 через sin та cos.
Подати sin3 та cos3 через sin та cos.
![]()
![]()
Прирівнюючи відповідні абсциси та ординати, дістаємо:
![]()
![]() .
.
2. Якщо р = 1/n, маємо:
|
k = 0, 1, 2, …, n – 1. |
(4) |
![]() Знайти
Знайти ![]() .
.
За формулою (3) ![]() ,
, ![]() . Далі згідно з (4) (рис. 1.16):
. Далі згідно з (4) (рис. 1.16):
|
|
Рис. 1.16 |
Показникова форма комплексного числа
Формула Ейлера: ![]()
Згідно з цією формулою комплексне число можна подати в показниковій формі:
|
|
(5) |
Справді, нехай r — модуль комплексного числа z = a + ib, а — головний аргумент. Тоді
z = r (cos + i sin).
Беручи до уваги формулу Ейлера, дістаємо:
![]()
Властивості:
|
|
![]() Обчислити дійсне значення
Обчислити дійсне значення ![]() .
.
![]() .
.
Самостійне вивчення №3
Тема: Визначники другого і третього порядків та їх властивості. Мінор та алгебраїчне доповнення. Методи обчислення визначників. Матриці. Дії над матрицями. Обернена матриця.
Література: О-1 с. 7-13, 9-24; О-2 с. 73-96; О-4 с. 213-229;
О-5 с. 63-81; Д-5 с. 7-26; Д-6 с. 3-25.
В результаті самостійного вивчення студенти повинні
знати:
- означення визначника другого та третього порядків;
- властивості визначників;
- означення мінору та алгебраїчного доповнення елемента визначника;
- означення матриці, види матриць;
вміти:
- обчислювати визначники другого та третього порядків;
- обчислювати мінори та алгебраїчні доповнення елементів визначника;
- виконувати дії над матрицями;
- знаходити обернену матрицю.
Короткі теоретичні відомості та методичні вказівки
Означення визначника
Нехай А — квадратна матриця розміру nn:
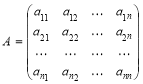 .
.
Означення. Визначником матриці А n-го порядку називається алгебраїчна сума всіх можливих добутків n елементів матриці, узятих по одному з кожного її рядка і кожного стовпця. Якщо в кожному добутку перші індекси розміщені в порядку зростання, то знак добутку дорівнює (–1)s, де s — число інверсій у переставленні других індексів.
Визначник подається виразом
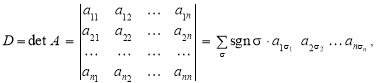 (1)
(1)
де ![]() — переставлення чисел
— переставлення чисел ![]() . Вираз (1) називається визначником n-го порядку, числа
. Вираз (1) називається визначником n-го порядку, числа ![]() — його елементами; горизонтальні послідовності чисел називаються рядками визначника, а вертикальні — його стовпцями. Ряд чисел
— його елементами; горизонтальні послідовності чисел називаються рядками визначника, а вертикальні — його стовпцями. Ряд чисел ![]() називається головною діагоналлю визначника.
називається головною діагоналлю визначника.
Якщо в (1) переставимо елементи ![]() довільним чином, то ця формула набере вигляду
довільним чином, то ця формула набере вигляду
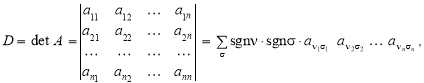
де ![]() — переставлення чисел
— переставлення чисел ![]() .
.
Отже, якщо переставлення перших індексів ![]() і других індексів
і других індексів ![]() мають однакову парність, то відповідний доданок береться зі знаком «+», а якщо різну, то відповідний доданок береться зі знаком «–».
мають однакову парність, то відповідний доданок береться зі знаком «+», а якщо різну, то відповідний доданок береться зі знаком «–».
Згідно з цим означенням знайдемо вираз для визначника другого порядку:
![]() .
.
Оскільки можна скласти два різні добутки елементів визначника, що беруться по одному з кожного рядка і стовпця, то
![]()
 . (2)
. (2)
Усього існує 6 різних добутків елементів визначника, що беруться по одному з кожного рядка і кожного стовпця.
Згідно з (1) дістанемо вираз:
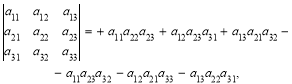
що являє собою визначник третього порядку.
Існує простий спосіб розкриття визначника третього порядку — так зване правило Саррюса. Допишемо до визначника (2) перший і другий стовпці, а далі перемножатимемо елементи, що розміщені на одній лінії, як показано на схемі:
![]()
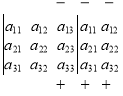
Добуток елементів, які розміщені на лініях, що йдуть згори ліворуч униз праворуч, береться зі знаком «+». Добуток елементів, розміщених на лініях, що йдуть згори праворуч униз ліворуч, береться зі знаком «–».
![]() Обчислимо визначник третього порядку
Обчислимо визначник третього порядку
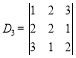 .
.
За правилом Саррюса складемо таблицю
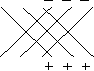

і знайдемо значення визначника:
D3 = 1 2 2 + 2 1 3 + 3 2 1 – 3 2 3 – 1 1 1 – 2 2 2 = –11.
Оскільки визначник n-го порядку складається з n! доданків, то формула (1) не застосовується для обчислення визначників при n > 3 (уже при n = 4 визначник містить 4! = 24 доданки).
Для обчислення визначників застосовують властивості, що розглядаються далі.
Властивості визначників
Властивість 1. При транспонуванні визначника його значення не змінюється.
Доведення. Доведемо, що визначники
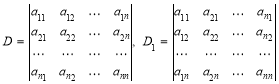
рівні. Розглянемо доданки, які входять до D:
![]() .
.
Якщо позначити ![]() , то до визначника D1 увійде відповідний доданок
, то до визначника D1 увійде відповідний доданок
![]() .
.
Оскільки до визначників D та D1 входять однакові доданки з однаковими знаками, то D = D1.
Із властивості 1 випливає, що рядки та стовпці визначника рівноправні. Усі наведені далі властивості, що справджуються для рядків, виконуються й для стовпців.
![]() Для визначника другого порядку маємо:
Для визначника другого порядку маємо:
![]() .
.
Властивість 2. Якщо всі елементи деякого рядка дорівнюють нулю, то визначник дорівнює нулю.
Доведення. Оскільки кожний із доданків, що входять до визначника, містить нульовий множник, то всі доданки дорівнюють нулю і визначник також дорівнює нулю.
![]()
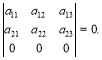
Властивість 3. Якщо всі елементи будь-якого рядка мають спільний множник, то його можна винести за знак визначника.
Доведення. Кожний із доданків, що входять до визначника, містить один із елементів розглядуваного рядка. Тому спільний множник елементів цього рядка можна виносити із суми цих доданків.
![]() Обчислимо визначник:
Обчислимо визначник:
 .
.
Властивість 4. Якщо поміняємо місцями два рядки визначника, то він змінить свій знак.
Доведення. У визначнику n-го порядку поміняємо місцями k-й і s-й рядки (s > k). Здобутий визначник позначимо D1. Якщо до визначника D входить доданок
![]() ,
,
то до визначника D1 обов’язково входить аналогічний доданок
![]() .
.
Оскільки переставлення других індексів відрізняються однією транспозицією, то парність переставлень різна. Отже, доданок, що є добутком розглядуваних елементів, завжди входить до визначників D та D1 з різними знаками. Це й доводить потрібну властивість.
![]() Поміняємо місцями рядки у визначнику:
Поміняємо місцями рядки у визначнику:
![]() .
.
Властивість 5. Якщо у визначнику два рядки однакові, то визначник дорівнює нулю.
Доведення. Поміняємо місцями однакові рядки визначника. Він при цьому не зміниться, а згідно з властивістю 4 лише змінить свій знак, тобто D = –D. Звідси випливає, що D = 0.
![]() Для визначника третього порядку виконується рівність:
Для визначника третього порядку виконується рівність:
 ,
,
оскільки цей визначник має два однакові рядки.
Властивість 6. Якщо у визначнику елементи одного рядка пропорційні до відповідних елементів іншого рядка, то визначник дорівнює нулю.
Доведення. Винесемо множник пропорційності за знак визначника й дістанемо визначник з двома однаковими рядками, який дорівнює нулю.
Властивість 7. Якщо у визначнику D всі елементи будь-якого рядка є сумою двох доданків, то цей визначник є сумою двох визначників, усі елементи яких (крім фіксованого рядка) збігаються. У першому визначнику фіксований рядок містить перші доданки, у другому визначнику фіксований рядок містить другі доданки.
Доведення. Візьмемо k-й рядок. Оскільки до кожного з доданків, що утворюють визначник, входить один із елементів k-го рядка, то можна в загальному вигляді записати розклад визначника за елементами цього рядка:
![]() .
.
Множники ![]() називаються алгебраїчними доповненнями елементів
називаються алгебраїчними доповненнями елементів ![]() . Якщо
. Якщо
ці елементи є сумами двох доданків ![]() то
то ![]()
![]()
що й доводить сформульовану властивість.
![]() За властивістю 7 маємо:
За властивістю 7 маємо:
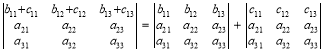 .
.
Властивість 8. Якщо до елементів деякого рядка визначника додати відповідні елементи іншого його рядка, помноживши на одне й те саме число, то значення визначника при цьому не зміниться.
Доведення. Додамо до елементів k-го рядка визначника D елементи s-го його рядка ![]() , помножені на число . Здобутий визначник набере такого вигляду D1:
, помножені на число . Здобутий визначник набере такого вигляду D1:
![]()
Останній доданок дорівнює нулю, бо визначник має однакові k-ті та s-ті рядки. Отже, D1 = D.
![]() Маємо рівність визначників:
Маємо рівність визначників:
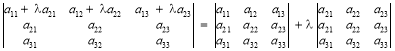 .
.
Із доведення властивостей 7 і 8 випливають розглянуті далі властивості визначників.
Властивість 9. Сума добутків елементів будь-якого рядка або стовпця визначника на відповідні алгебраїчні доповнення дорівнює цьому визначнику, тобто якщо
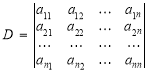 ,
,
то справджуються рівності:
![]()
Властивість 10. Сума добутків елементів будь-якого рядка визначника на алгебраїчне доповнення відповідних елементів іншого його рядка дорівнює нулю:
![]() .
.
Аналогічна властивість виконується для стовпців:
![]() .
.
Властивості 9 і 10 мають важливе значення, оскільки використовуються при обчисленні алгебраїчних доповнень, про що йтиметься далі.
Обчислення визначників
Обчислюючи визначники, можна ефективно застосовувати таку теорему.
Теорема 1. Якщо всі елементи визначника, розміщені вище або нижче від головної діагоналі, дорівнюють нулю, то визначник дорівнює добутку діагональних елементів.
Доведення. Єдиним доданком, який може бути відмінним від нуля, є добуток діагональних елементів, оскільки визначник є алгебраїчною сумою добутків його елементів, узятих по одному з кожного рядка та кожного сповпця. Маємо:
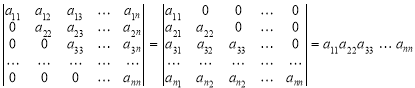 . (1)
. (1)
Щоб перетворити визначник до виду (1), застосуємо властивість 8.
![]() Обчислимо визначник третього порядку
Обчислимо визначник третього порядку
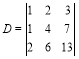 .
.
Знайдемо різницю першого і другого рядків, а потім помножимо перший рядок на 2 і віднімемо від третього рядка. Дістанемо визначник
 .
.
Віднявши другий його рядок від третього, дістанемо
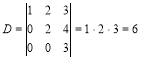 .
.
![]() Обчислимо визначник четвертого порядку
Обчислимо визначник четвертого порядку
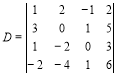 .
.
Додамо перший рядок до другого і четвертого, утворивши визначник
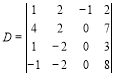 .
.
Поміняємо місцями перший і третій стовпці:
 .
.
Додамо другий рядок до третього і четвертого рядків і винесемо спільний множник елементів третього і четвертого рядків:
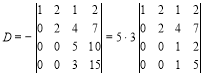 .
.
Віднявши третій рядок від четвертого, обчислимо даний визначник за формулою (1):
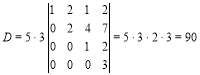 .
.
Матриці
Означення. Матрицею називається прямокутна таблиця чисел (дійсних або комплексних). Горизонтальні ряди чисел називаються рядками, вертикальні — стовпцями. Рядки нумеруються згори вниз, стовпці — зліва направо. Числа, що утворюють матрицю, називаються її елементами. Елементи матриці позначають малими латинськими буквами з подвійними індексами. Так, aks — елемент, який міститься в k-му рядку, s-му стовпці. Самі матриці позначають великими латинськими буквами:
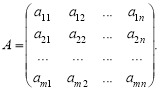
Якщо матриця має m рядків і n стовпців, то говорять, що вона має розмір m n. При цьому матрицю можна записати як вектор-рядок, компонентами якого є вектори-стовпці:
![]() ,
,
де
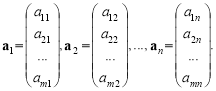
Аналогічно матрицю А можна подати як вектор-стовпець, компонентами якого є вектори-рядки:
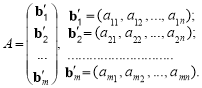
![]() Матрицю А розміру 3 4 можна подати у вигляді
Матрицю А розміру 3 4 можна подати у вигляді
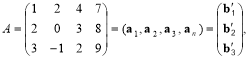
де
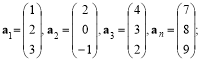
![]()
Кожний вектор можна розглядати як матрицю. Скажімо, вектор-рядок ![]() — це матриця розміру 1 n, а вектор-стовпець
— це матриця розміру 1 n, а вектор-стовпець ![]() — матриця розміру m 1.
— матриця розміру m 1.
Матриця називається нульовою, якщо її елементи дорівнюють нулю. Дві матриці називаються рівними, якщо вони мають однаковий розмір і в них рівні між собою однаково розміщені елементи.
Означення. Матриця називається квадратною, коли число її рядків дорівнює числу її стовпців. Якщо квадратна матриця має n стовпців, то говорять, що матриця має порядок n. Ряд чисел а11, а 22, …, аnn називається головною її діагоналлю.
Означення. Квадратна матриця називається діагональною, якщо всі її елементи, розміщені поза головною діагоналлю, дорівнюють нулю.
![]() Матриця А є діагональною
Матриця А є діагональною
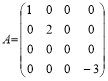 .
.
Означення. Діагональна матриця називається одиничною, якщо всі її елементи, розміщені на головній діагоналі, дорівнюють одиниці.
Одинична матриця позначається так:
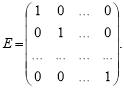
Одиничну матрицю можна подати через вектори ![]() канонічного базису:
канонічного базису:
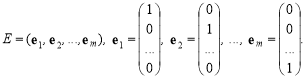
Означення. Транспонуванням матриці називається заміна її рядків на стовпці зі збереженням порядку їх запису.
Операцію транспонування позначають буквою Т у показнику степеня або штрихом:

![]()
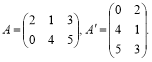
Очевидно, що справджується рівність
![]()
Діагональна матриця в результаті транспонування не змінюється. Зокрема, для одиничної матриці маємо
![]()
Означення. Матриця А називається симетричною, якщо
![]()
і кососиметричною, якщо
![]()
Для елементів ![]() симетричної матриці виконується рівність
симетричної матриці виконується рівність
![]()
Для елементів кососиметричної матриці
![]()
У кососиметричної матриці діагональні елементи дорівнюють нулю, оскільки akk = –akk (k = 1, 2, …, n).
Матриця А є симетричною, В — кососиметричною:
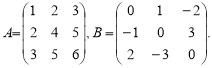
Означення. Квадратна матриця називається трикутною, якщо всі її елементи, розміщені під головною діагоналлю або над нею, дорівнюють нулю.
![]() Розглянемо дві матриці
Розглянемо дві матриці
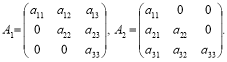
Матриця А1 називається верхньою трикутною, а матриця А2 — нижньою трикутною.
Дії з матрицями
Означення. Нехай дано матрицю А, розмір якої ![]() , і скаляр . Добутком на А називається матриця розміру
, і скаляр . Добутком на А називається матриця розміру ![]() :
:
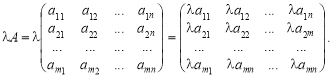
Щоб помножити матрицю А на скаляр , потрібно кожний її елемент помножити на цей скаляр.
![]()
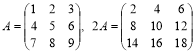 .
.
Означення. Сумою двох матриць

розміру ![]() є матриця
є матриця
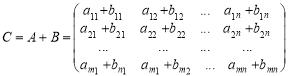
такого самого розміру. Аналогічно означується різниця матриць. Додавати і віднімати можна лише матриці однакового розміру.
![]() Знайдемо суму та різницю двох матриць
Знайдемо суму та різницю двох матриць
![]() :
:
![]() .
.
Згідно з наведеними означеннями виконуються такі правила:
Добуток матриць визначається через добуток лінійних перетворень. Нехай дано дві матриці: матрицю В розміру ![]() і матрицю А розміру
і матрицю А розміру ![]() :
:
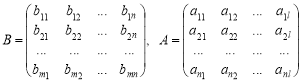 . (1)
. (1)
Розглянемо лінійні перетворення ![]() , які можна подати у вигляді
, які можна подати у вигляді
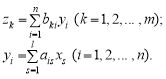
Виключаючи змінні ![]() , знаходимо лінійне перетворення
, знаходимо лінійне перетворення ![]() , яке можна записати так:
, яке можна записати так:
![]()
Позначивши
![]() , (2)
, (2)
подамо це лінійне перетворення у вигляді
![]() ,
,
або
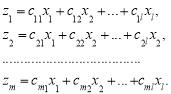
Останню систему зручно записувати у векторній формі ![]() , де матриця С розміру
, де матриця С розміру ![]() має вигляд
має вигляд
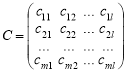 . (3)
. (3)
Означення. Матриця С виду (3) з елементами виду (2) називається добутком матриць В та А: С = ВА.
Елемент ![]() матриці С, що міститься в k-му рядку матриці В і s-му стовпці матриці А, є скалярним добутком k-го рядка матриці В та s-го стовпця матриці А.
матриці С, що міститься в k-му рядку матриці В і s-му стовпці матриці А, є скалярним добутком k-го рядка матриці В та s-го стовпця матриці А.
Добуток матриць ВА є визначеним лише в тому разі, коли число стовпців першого множника дорівнює числу рядків другого множника.
Добуток матриць В розміру ![]() та А розміру
та А розміру ![]() є матрицею, розмір якої
є матрицею, розмір якої ![]() :
:
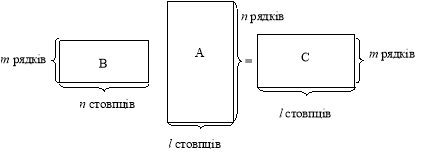
Рис. 2.5
![]() Знайдемо добуток матриць
Знайдемо добуток матриць
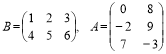 ;
;
![]() ;
;
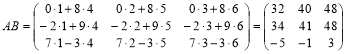 .
.
На цьому прикладі бачимо, що в загальному випадку ![]() .
.
Означення. Якщо АВ = ВА, то матриці А, В називаються переставними, або комутативними.
Наведемо властивості добутку матриць, припускаючи, що множення їх можливе.
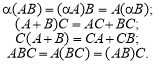
Якщо Е — одинична матриця, то ЕА = А, АЕ = А.
При транспонуванні матриць справджуються рівності:
![]() .
.
Добуток матриці А на вектор-стовпець ![]() можна розглядати як частинний випадок добутку матриці А розміру
можна розглядати як частинний випадок добутку матриці А розміру ![]() на матрицю розміру
на матрицю розміру ![]()
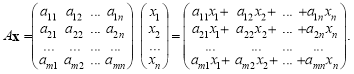
Скалярний добуток ![]() двох векторів-стовпців можна роз-
двох векторів-стовпців можна роз-
глядати як матричний добуток транспонованого вектора ![]() на вектор
на вектор ![]() :
:

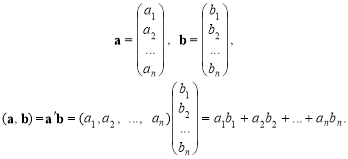
Самостійне вивчення №4
Тема: Системи лінійних рівнянь з двома і трьома змінними. Критерії сумісності системи лінійних рівнянь – теорема Кронекера-Капеллі. Основні методи розв’язування систем лінійних рівнянь: метод Гауса, за формулами Крамера, матричним способом. Прикладні задачі курсів спецдисциплін, які приводять до системи лінійних рівнянь, та їх розв’язання.
Література: О-1 с.14-19, 24-28; О-2 с. 99-113; О-4 с. 230-240;
О-5 с. 81-91; Д-5 с. 27-37; Д-6 с. 25-35.
В результаті самостійного вивчення студент повинен
знати:
- означення системи лінійних рівнянь з двома і трьома змінними;
- критерії сумісності системи лінійних рівнянь.
вміти:
- розв’язувати системи лінійних рівнянь за формулами Крамера;
- розв’язувати системи лінійних рівнянь методом Гауса;
- розв’язувати системи лінійних рівнянь матричним методом.
Короткі теоретичні відомості та методичні вказівки
Розглянемо систему m лінійних рівнянь з n невідомими:
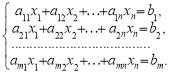 (1)
(1)
Означення. Розв’язком системи (1) називається сукупність значень невідомих
![]()
що задовольняють усі рівняння системи (1).
Означення. Система рівнянь (1) називається сумісною, якщо вона має принаймні один розв’язок, і несумісною, якщо вона не має розв’язків.
Система рівнянь називається визначеною, якщо вона має лише один розв’язок, і невизначеною, якщо вона має безліч розв’язків.
Дві системи рівнянь з однаковими невідомими називаються рівносильними, якщо кожний розв’язок однієї системи є розв’язком іншої системи або якщо ці системи рівнянь несумісні.
У результаті еквівалентних перетворень системи рівнянь завжди дістаємо рівносильну систему рівнянь. До еквівалентних перетворень системи належать:
1) переставлення місцями рівнянь;
2) множення або ділення рівнянь на число, що не дорівнює нулю;
3) додавання до деякого рівняння іншого рівняння, помноженого на довільне число.
Будь-який метод розв’язування системи рівнянь (1) передбачає виконання еквівалентних її перетворень, завдяки яким вона зводиться до такого вигляду, що розв’язок уже легко знайти.
Запишемо вектори-стовпці
 . (2)
. (2)
Для того щоб система рівнянь (1) була сумісною, тобто мала принаймні один розв’язок, необхідно і достатньо, щоб вектор ![]() був лінійною комбінацією векторів
був лінійною комбінацією векторів ![]() , тобто щоб ранг r системи векторів
, тобто щоб ранг r системи векторів ![]() дорівнював рангу розширеної системи векторів
дорівнював рангу розширеної системи векторів ![]() .
.
Звідси дістаємо умову Кронекера—Капеллі сумісності системи рівнянь.
Для того щоб система (1) була сумісною, необхідно і достатньо, щоб ранг r матриці
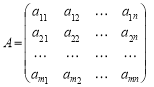 (3)
(3)
![]() дорівнював рангу розширеної матриці
дорівнював рангу розширеної матриці
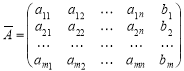 .
.
Нехай система рівнянь (1) сумісна, тобто виконується рівність
![]() .
.
Якщо, ![]() , то всі рівняння системи (1) лінійно незалежні. У матриці А візьмемо мінор порядку
, то всі рівняння системи (1) лінійно незалежні. У матриці А візьмемо мінор порядку ![]() , відмінний від нуля. Цей мінор називається базисним.
, відмінний від нуля. Цей мінор називається базисним.
Очевидно, що вибір базисного мінора неоднозначний. Якщо ![]() , то рівняння, коефіцієнти яких входять до базисного мінора, лінійно незалежні, причому решта
, то рівняння, коефіцієнти яких входять до базисного мінора, лінійно незалежні, причому решта ![]() рівнянь є лінійними комбінаціями лінійно незалежних рівнянь.
рівнянь є лінійними комбінаціями лінійно незалежних рівнянь.
Якщо ![]() , то всі шукані змінні
, то всі шукані змінні ![]() визначаються єдиним чином. Якщо
визначаються єдиним чином. Якщо ![]() , то змінні, коефіцієнти при яких входять до базисного мінора, називаються базисними.
, то змінні, коефіцієнти при яких входять до базисного мінора, називаються базисними.
Решту змінних називають вільними. Значення таких змінних можна вибирати довільно. Якщо вільні змінні вибрано, то базисні змінні можна вибрати єдиним чином. Якщо вільні невідомі дорівнюють нулю, то відповідний розв’язок системи (1) називається базисним.
Розглянемо однорідну систему рівнянь, що відповідають системі (1):
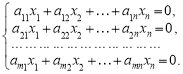 (4)
(4)
Вона сумісна, бо завжди має нульовий розв’язок ![]()
![]() . Якщо
. Якщо ![]() , то система (4) має єдиний нульовий розв’язок. Якщо
, то система (4) має єдиний нульовий розв’язок. Якщо ![]() , то система (4) має
, то система (4) має ![]() лінійно незалежних ненульових розв’язків:
лінійно незалежних ненульових розв’язків:
![]() . (5)
. (5)
Будь-яка лінійна комбінація розв’язків
![]() (6)
(6)
також є розв’язком системи рівнянь (4).
Якщо всі розв’язки (5) лінійно незалежні, тобто ранг матриці
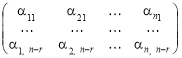
дорівнює (![]() ), то система розв’язків (5) називається фундаментальною.
), то система розв’язків (5) називається фундаментальною.
Будь-який розв’язок системи рівнянь (4) можна подати у вигляді (6), тобто у вигляді лінійної комбінації розв’язків (5), які утворюють фундаментальну систему розв’язків.
При цьому розв’язок (6) системи рівнянь (4) називається загальним розв’язком однорідної системи (4).
Загальний розв’язок системи (1) є сумою деякого частинного розв’язку цієї системи, наприклад базисного розв’язку, і загального розв’язку однорідної системи рівнянь (4).
![]() Розглянемо систему п’яти лінійних рівнянь з чотирма невідомими
Розглянемо систему п’яти лінійних рівнянь з чотирма невідомими
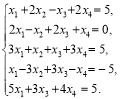 (7)
(7)
Можна переконатися, що ранг матриці коефіцієнтів і ранг розширеної матриці дорівнюють r = 2. За базисний мінор візьмемо визначник
![]() ,
,
елементи якого входять до перших двох рівнянь і є коефіцієнтами при ![]() . Отже, базисними невідомими є
. Отже, базисними невідомими є ![]() , вільними невідомими —
, вільними невідомими — ![]() .
.
Замість системи (7) можна розв’язати систему, утворену з двох перших рівнянь:
![]() (8)
(8)
Візьмемо вільні невідомі ![]() і
і ![]() , а далі знайдемо базисний розв’язок системи рівнянь (7):
, а далі знайдемо базисний розв’язок системи рівнянь (7): ![]() .
.
Вважаючи х3 і х4 довільними змінними, із системи рівнянь
![]()
знайдемо розв’язки

Нехай ![]() , де С1, С2 — довільні сталі. Тоді загальний розв’язок
, де С1, С2 — довільні сталі. Тоді загальний розв’язок
![]()
Запишемо однорідну систему рівнянь
![]() (9)
(9)
Вона має лінійно незалежні розв’язки:
![]()
які утворюють фундаментальну систему розв’язків системи (5).
Отже, система рівнянь (7) має загальний розв’язок
![]()
де С1, С2 — довільні сталі.
Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді.
Самостійне вивчення №5
Тема: Поняття вектора. Дії над векторами. Векторні простори. Проекція вектора на вісь. Базис на площині і в просторі. Поділ відрізка в даному відношенні. Розкладання вектора за базисом.
Література: О-1 с. 28-30; О-2 с. 125-137; О-5 с. 125-134; Д-6 с. 38-46.
В результаті самостійного вивчення студент повинен
знати:
- означення вектора;
- види векторів;
вміти:
- виконувати дії над векторами;
- розкладати вектор за базисом;
Короткі теоретичні відомості та методичні вказівки
Вектором у просторі, як і на площині, називається напрямлений відрізок.
Позначення вектора:
Вектор, початок і кінець якого співпадають (є однією точкою), називається нульовим вектором або нуль-вектором. Будь-яка точка простору може розглядатися як нульовий вектор. Напрям нульового вектора не визначений.
Позначення нуль-вектора: ![]() .
.
Два вектори в просторі називаються рівними, якщо вони однаково напрямлені і мають однакову довжину.
![]() Щоб знайти координати вектора потрібно від координат кінця вектора відняти координати його початку.
Щоб знайти координати вектора потрібно від координат кінця вектора відняти координати його початку.
Якщо А(x1;y1;z1), B (x2;y2;z2), то
- Всі координати нульового вектора дорівнюють нулю.
- Координати вектора не змінюються при паралельному перенесенні.
- Рівні вектори мають рівні відповідні координати.
![]() Модулем (абсолютною величиною) вектора називається довжина відрізка, що містить вектор.
Модулем (абсолютною величиною) вектора називається довжина відрізка, що містить вектор.
Позначення:
Якщо вектор ![]() , то
, то ![]() .
.
Модуль нульового вектора дорівнює нулю.
Рівні вектори мають рівні модулі.
Два ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Якщо вектори ![]() та
та ![]() колінеарні, то їх координати пропорційні:
колінеарні, то їх координати пропорційні:![]() .
.
Над векторами в просторі визначено шість операцій (дій):
- додавання векторів (сума векторів);
- віднімання векторів (різниця векторів);
- множення вектора на число (скаляр) (добуток вектора на число (скаляр);
- скалярний добуток двох векторів;
- векторний добуток двох векторів;
- мішаний добуток трьох векторів.
Означення. Сумою a + b векторів a та b називається вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (рис. 3.10).
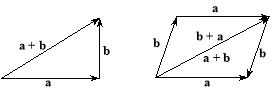
Рис. 3.10 Рис. 3.11
Додавання векторів комутативне, тобто для довільних векторів a і b справджується рівність (рис. 3.11)
a + b = b + a. (1)
Додавання векторів асоціативне, тобто для будь-яких векторів a, b, c виконується рівність
(a + b) + c = a + (b + c). (2)
Цю властивість, що випливає з означення суми векторів, унаочнює рис. 3.12.

Рис. 3.12
Віднімання векторів — операція, обернена до їх додавання. Різниця b – a векторів a і b являє собою вектор, початок якого збігається з початком вектора a, а кінець — із кінцем вектора b (рис. 3.13).
a + (b – a) = b

Рис. 3.13
Для будь-яких векторів a, b виконуються нерівності:
![]() .
.
Розглянемо довільний вектор a і вісь х.
Означення. Якщо вектор a утворює кут з віссю х (рис. 3.14), то проекцією вектора а на вісь називається величина
![]() . (3)
. (3)
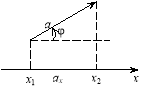
Рис. 3.14
Якщо х1 — координата проекції початку вектора, а х2 — координата проекції кінця вектора на вісь х, то
![]() (4)
(4)
Нехай вектор а має початок у точці М1(х1, y1, z1), а кінець — у точці М2(х2, y2, z2). Тоді величини
![]()
є проекціями вектора a на осі х, y, z. Проекції вектора однозначно визначають вектор. Тому виконується рівність
![]()
Очевидно, що проекція на вісь х суми a + b векторів a та b дорівнює сумі проекцій на вісь х векторів a, b (рис. 3.15).
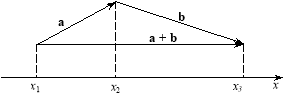
Рис. 3.15
● Справді, виконуються рівності
![]()
Нехай відомі проекції векторів a та b:
![]() .
.
Тоді проекція суми векторів a + b дорівнює сумі відповідних проекцій векторів-доданків:
![]()
Означення. Добутком вектора a на число називається вектор ![]() , довжина якого дорівнює
, довжина якого дорівнює ![]() . Вектор
. Вектор ![]() колінеарний вектору а; має однаковий з ним напрям при
колінеарний вектору а; має однаковий з ним напрям при ![]() і протилежний напрям при
і протилежний напрям при ![]() . Якщо
. Якщо ![]() або
або ![]() , то маємо
, то маємо ![]() , тобто добуток є нуль-вектором.
, тобто добуток є нуль-вектором.
Множення вектора на число має властивість асоціативності та дистрибутивності. Для довільних чисел , та векторів a, b справджуються рівності:
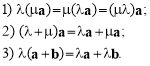 (1)
(1)
Останню рівність унаочнює рис. 3.16 (![]() ).
).
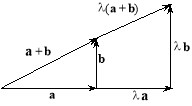
Ця властивість випливає з подібності трикутників із коефіцієнтом подібності .
З очевидної рівності
![]()
випливає:
![]()
Лема. Будь-який вектор a можна єдиним чином подати у вигляді суми трьох векторів, кожний із яких колінеарний одній з осей координат х, у, z.
Справді, нехай М1 — початок вектора a, М2 — його кінець. Сумістимо точку М1 із початком координат. Опустимо з точки М2 перпендикуляр на координатну площину ху і позначимо здобуту проекцію М3. Із точки М3 опустимо перпендикуляр на вісь х. Відповідну проекцію позначимо М4. Вектор М3М2 колінеарний осі z, вектор М4М3 — осі у, а вектор М1М4 — осі х.
Звідси, скориставшись одиничними векторами i, j, k, що, як відомо, колінеарні осям х, у, z, дістанемо:
![]() .
.
Оскільки виконується рівність ![]() (рис. 3.17),
(рис. 3.17),
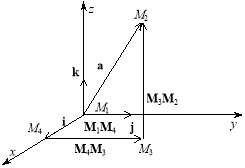
Рис. 3.17
то вектор a можна записати у вигляді:
![]() (2)
(2)
Вектори ![]() називаються компонентами вектора a.
називаються компонентами вектора a.
Отже, кожний вектор дорівнює сумі його компонентів за трьома осями координат.
Якщо вектори a та b подано за їх компонентами:![]()
то для їх лінійної комбінації маємо
![]() . (3)
. (3)
Самостійне вивчення №6
Тема: Скалярний добуток векторів. Кут між векторами. Напрямні косинуси. Умови колінеарності і компланарності векторів. Векторний і мішаний добуток векторів.
Література: О-2 с. 132-134; О-5 с. 136-139; Д-6 с. 46-51.
В результаті самостійного вивчення студент повинен
знати:
- формули для обчислення скалярного, векторного та мішаного добутку векторів;
- формулу для визначення кута між векторами.
вміти:
- знаходити скалярний, векторний та мішаний добуток векторів;
- визначати кут між векторами.
Короткі теоретичні відомості та методичні вказівки
Скалярний добуток векторів
Означення. Скалярним добутком векторів a і b називається число ![]() , що дорівнює добутку довжини цих векторів на косинус кута між ними (рис. 3.18):
, що дорівнює добутку довжини цих векторів на косинус кута між ними (рис. 3.18):
![]() (1)
(1)
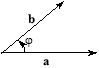
Рис. 3.18
Нехай ![]() — проекція вектора b на вісь, паралельну вектору a. Тоді маємо:
— проекція вектора b на вісь, паралельну вектору a. Тоді маємо:
![]() (2)
(2)
Останнє співвідношення означає, що скалярний добуток двох векторів дорівнює модулю одного з них, помноженому на проекцію другого вектора на напрям першого.
Якщо кут між векторами a та b гострий, то ![]() ; якщо тупий, то
; якщо тупий, то ![]() ; якщо прямий, то
; якщо прямий, то ![]() . Коли один із векторів a, b є нульовим, то його можна вважати ортогональним до будь-якого іншого вектора.
. Коли один із векторів a, b є нульовим, то його можна вважати ортогональним до будь-якого іншого вектора.
Наведемо аналітичні властивості скалярного добутку, що випливають із його означення.
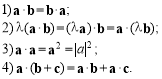
Остання рівність є наслідком формули (2) і властивості проекцій суми векторів:
![]()
Отже, у разі скалярного множення суми векторів на вектор можна розкривати дужки. Нехай вектори а та b подано через їх проекції на координатні осі:
![]()
Запишемо таблицю скалярного множення для одиничних векторів i, j, k — ортів системи координат:
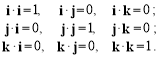
Перемноживши скалярно вектори a та b, знайдемо їх скалярний добуток у проекціях на координатні осі:
![]() (3)
(3)
Звідси маємо:
![]()
Знаючи проекції векторів а, b, можна знайти кут між цими векторами:
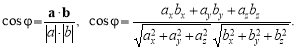
![]() Дано просторовий трикутник з вершинами А(1, 2, –1),
Дано просторовий трикутник з вершинами А(1, 2, –1),
В(2, 4, 1), С(3, 0, 0). Знайдемо кут при вершині А.
Розглянемо вектори
![]()
і з їх скалярного добутку визначимо косинус шуканого кута:
![]() .
.
Оскільки скалярний добуток векторів a, b дорівнює нулю, то кут при вершині А прямий.
Позначимо , , кути між осями координат х, у, z та вектором a. Ці кути називаються напрямними кутами. Проекції вектора a на координатні осі подаються так:
![]() (4)
(4)
Величини ![]() називаються напрямними косинусами вектора a. Згідно з (4) маємо:
називаються напрямними косинусами вектора a. Згідно з (4) маємо:
![]() (5)
(5)
![]() Розглянемо вектор a у площині ху, який утворює кут 60 з віссю х і кут 30 з віссю у. Знайдемо напрямні косинуси вектора a:
Розглянемо вектор a у площині ху, який утворює кут 60 з віссю х і кут 30 з віссю у. Знайдемо напрямні косинуси вектора a:
![]() .
.
![]() Доведемо теорему косинусів для трикутника.
Доведемо теорему косинусів для трикутника.
Позначивши сторони трикутника векторами a, b, c (рис. 3.19), подамо вектор c через вектори a та b: c = b – a. Далі, виконавши перетворення, дістанемо шукану залежність — відому теорему косинусів:
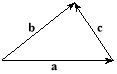
Рис. 3.19
![]()
Векторний добуток векторів
Означення. Векторним добутком векторів a та b називається вектор ![]() , який задовольняє такі умови:
, який задовольняє такі умови:
-
вектор
 перпендикулярний до векторів a і b;
перпендикулярний до векторів a і b;
-
довжина
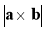 вектора
вектора 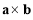 дорівнює площі паралелограма, побудованого на векторах a та b;
дорівнює площі паралелограма, побудованого на векторах a та b;
-
якщо звести вектори a, b та
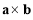 до спільного початку, то спостерігач, який міститься в кінці вектора
до спільного початку, то спостерігач, який міститься в кінці вектора 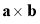 , бачитиме найкоротший поворот від вектора a до вектора b таким, що відбувається проти годинникової стрілки (рис. 3.20).
, бачитиме найкоротший поворот від вектора a до вектора b таким, що відбувається проти годинникової стрілки (рис. 3.20).
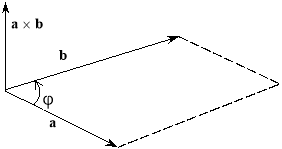
Рис. 3.20
З означення векторного добутку випливають такі його властивості
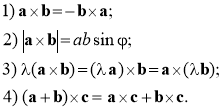
Перші три властивості очевидні, останню властивість дистрибутивності наводимо без доведення.
Знайдемо векторний добуток векторів
![]() .
.
Запишемо таблицю множення ортів i, j, k:
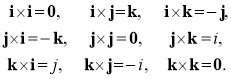
Виконавши відповідні перетворення, дістанемо:
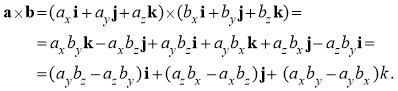
Векторний добуток векторів a та b можна подати у вигляді визначника:
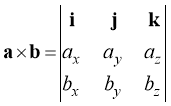 (1)
(1)
☺Приклад Знайдемо площу просторового трикутника з вершинами А(1, 2, 1), В(4, 3, 2), С(2, 4, 4).
Позначаючи вектори
![]() ,
,
обчислюємо їх векторний добуток:
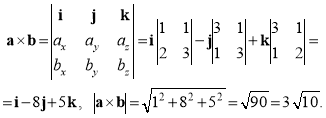
Площа S трикутника АВС дорівнює половині площі паралело-
грама, побудованого на векторах a, b:
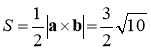 .
.
Мішаний добуток векторів
Означення. Мішаним добутком векторів a, b, c називається число
![]()
Мішаний добуток за модулем дорівнює об’єму паралелепіпеда, побудованого на векторах a, b, c.
Справді, позначимо ![]() .
.
Вектор d перпендикулярний до основи паралелепіпеда, а довжина його ![]() дорівнює площі S паралелограма, побудованого на векторах a та b як на сторонах (рис. 3.21).
дорівнює площі S паралелограма, побудованого на векторах a та b як на сторонах (рис. 3.21).

Рис. 3.21
Висота h паралелепіпеда дорівнює ![]() . Отже, об’єм його обчислюємо так:
. Отже, об’єм його обчислюємо так:
![]()
Оскільки вектор d може бути напрямлений у протилежний бік, то ![]() .
.
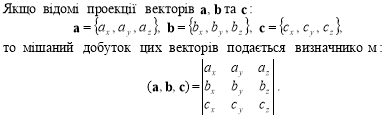 (1)
(1)
Звідси маємо:
![]() .
.
![]() Знайдемо об’єм V тетраедра з вершинами А(1, 2, 3),
Знайдемо об’єм V тетраедра з вершинами А(1, 2, 3),
В(4, 4, 4), С(2, 6, 4), D(2, 3, 6).
Розглянемо вектори
![]()
і запишемо їх мішаний добуток:
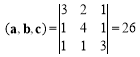 .
.
Шуканий об’єм тетраедра АВСD становить ![]() від об’єму паралелепіпеда, побудованого на векторах a, b, c. Отже,
від об’єму паралелепіпеда, побудованого на векторах a, b, c. Отже,
![]() .
.
Самостійне вивчення №7
Тема: Пряма лінія в просторі. Різні види рівнянь прямої в просторі. Кут між двома прямими в просторі. Кут між прямою і площиною. Умова перпендикулярності і паралельності прямої і площини.
Поняття про лінії другого порядку на площині. Загальне рівняння лінії другого порядку на площині. Коло. Еліпс. Гіпербола. Парабола. Застосування властивостей кривих другого порядку до розв’язування прикладних задач, зокрема задач економічного змісту.
Література: О-1 с. 125-131; О-2 с. 152-158, 164-167;
О-5 с. 152-160; О-6 с.50-85.
В результаті самостійного вивчення студент повинен
знати:
- різні види рівнянь прямої в просторі;
- формули для обчислення кута між двома прямими, між прямою та площиною;
- умови паралельності та перпендикулярності прямої та площини;
- рівняння кола, еліпса, гіперболи та параболи.
вміти:
- складати рівняння прямої в просторі;
- обчислювати кут між прямими, кут між прямою та площиною.
- складати рівняння кривих другого порядку.
Короткі теоретичні відомості та методичні вказівки
Рівняння прямої у просторі
Будь-яка пряма лінія у просторі подається системою двох рівнянь які задають (коли розглядати кожне з них зокрема) дві різні площини, що проходять через цю пряму.
![]() (1)
(1)
Рівняння (1), узяті разом, називаються загальними рівняннями прямої. Напрямний вектор ![]() цієї прямої ортогональний до кожної з нормалей
цієї прямої ортогональний до кожної з нормалей
![]()
Отже, можна вважати що
![]()
Щоб перейти від загальних рівнянь прямої до канонічного її рівняння, достатньо взяти дві різні точки на прямій і скористатися рівнянням (2) із підрозд. 3.5.6.
![]() Перейдемо від загального рівняння прямої
Перейдемо від загального рівняння прямої
![]()
до канонічного.
Візьмемо ![]() , та із системи рівнянь
, та із системи рівнянь ![]() ,
, ![]() знайдемо х1 = 1, у1 = – 5.
знайдемо х1 = 1, у1 = – 5.
Покладемо ![]() , то із системи рівнянь
, то із системи рівнянь ![]() ,
, ![]() знайдемо х2 = 1, у2 = – 7. Канонічне рівняння прямої набере вигляду
знайдемо х2 = 1, у2 = – 7. Канонічне рівняння прямої набере вигляду
![]() .
.
Щоб дістати довільну площину, яка проходить через пряму (1), застосовують пучок площин:
![]() . (2)
. (2)
Теорема. Коли площини (1) не паралельні, то вибором параметра в рівнянні (2) можна утворити будь-яку площину, що проходить через пряму (1), окрім другої площини.
![]() Складемо рівняння площини, яка проходить через пряму
Складемо рівняння площини, яка проходить через пряму ![]() і точку М1(1, 1, 1).
і точку М1(1, 1, 1).
Знаходимо загальні рівняння прямої
![]()
або
![]() .
.
Утворимо пучок площин
![]()
і визначимо ту з них, якій належить точка М1(1, 1, 1). Маємо
![]()
Остаточно запишемо рівняння шуканої площини:
![]()
![]() Знайти проекцію прямої, заданої рівняннями
Знайти проекцію прямої, заданої рівняннями ![]() на площину
на площину ![]() .
.
Утворимо пучок площин
![]()
і візьмемо в ньому таку площину, яка ортогональна до площини проектування:
![]()
Остаточно записуємо загальне рівняння проекції:
![]()
Пряма і площина у просторі
Дано площину
![]() ,
,
а також пряму з канонічним рівнянням
![]()
Знайдемо кут між цією прямою і заданою площиною. Обчислимо насамперед кут ![]() між вектором нормалі n і напрямленим вектором прямої s (рис. 3.51).
між вектором нормалі n і напрямленим вектором прямої s (рис. 3.51).
![]() .
.

Рис. 3.51
Згідно зі співвідношенням
![]()
маємо:
![]() (1)
(1)
Умова паралельності площини та прямої:
![]() ,
, ![]() . (2)
. (2)
Умова перпендикулярності прямої і площини:
![]() . (3)
. (3)
Щоб знайти точку перетину прямої і площини, скористаємося параметричними рівняннями прямої (3) із підрозд. 3.5.6. Підставляючи х, у, z у рівняння площини, дістаємо рівняння для t:
![]() . (4)
. (4)
1. Якщо ![]() , тобто пряма не паралельна площині, то пряма і площина перетинаються в одній точці.
, тобто пряма не паралельна площині, то пряма і площина перетинаються в одній точці.
2. Якщо ![]() , то пряма паралельна площині. Якщо
, то пряма паралельна площині. Якщо ![]() , тобто точка М0(х0, у0, z0) на прямій не лежить на площині, то рівняння (4) не має розв’язків. При цьому пряма проходить на деякій ненульовій відстані від площини.
, тобто точка М0(х0, у0, z0) на прямій не лежить на площині, то рівняння (4) не має розв’язків. При цьому пряма проходить на деякій ненульовій відстані від площини.
3. Якщо ![]() , то рівняння (4) виконується при всіх значеннях t. Усі точки на прямій належать площині.
, то рівняння (4) виконується при всіх значеннях t. Усі точки на прямій належать площині.
![]() Знайти проекцію точки М0(1, 2, 3) на площину
Знайти проекцію точки М0(1, 2, 3) на площину ![]() .
.
Для розв’язування задачі достатньо з точки М0 опустити на площину перпендикуляр і знайти точку його перетину з площиною (рис. 3.52).
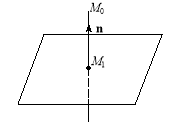
Рис. 3.52
Напрямний вектор прямої s колінеарний до вектора n нормалі до площини. Маємо ![]() . Отже, рівняння перпендикуляра:
. Отже, рівняння перпендикуляра:
![]() .
.
Підставивши вирази
![]()
у рівняння площини, дістанемо t
![]()
З параметричних рівнянь прямої знаходимо координати точки проекції М1(х1, у1, z1)
![]()
Криві другого порядку
Означення. Кривою другого порядку називається геометричне місце точок площини, координати яких задовольняють рівняння
![]() (1)
(1)
де хоча б один із коефіцієнтів ![]() відмінний від нуля.
відмінний від нуля.
Розглянемо квадратичну форму
![]()
а далі знайдемо власні числа матриці
![]()
з рівняння
![]() . (2)
. (2)
Позначимо корені рівняння (2) , і ортогональною заміною змінних
![]()
де вектори ![]() — власні вектори матриці А, перетворимо рівняння (1) до такого вигляду:
— власні вектори матриці А, перетворимо рівняння (1) до такого вигляду:
![]() . (3)
. (3)
Нехай ![]() , тоді, виділяючи повний квадрат і переміщуючи початок координат, дістанемо рівняння кривої
, тоді, виділяючи повний квадрат і переміщуючи початок координат, дістанемо рівняння кривої
![]() (4)
(4)
1. Якщо ![]() , то
, то ![]() .
.
Припустимо, що ![]() . При
. При ![]() , при
, при ![]() , а при
, а при ![]() .
.
Точку можна розглядати як граничний випадок еліпса.
2. Якщо ![]() , то
, то ![]() . Тоді при
. Тоді при ![]() , а при
, а при ![]() .
.
3. Якщо в рівнянні (3) ![]() , тобто
, тобто ![]() , то, узявши, наприклад, = 0, прийдемо до рівняння
, то, узявши, наприклад, = 0, прийдемо до рівняння
![]() . (5)
. (5)
При ![]() виділенням повного квадрата можна звести рівняння (5) до вигляду
виділенням повного квадрата можна звести рівняння (5) до вигляду
![]()
Отже, дістали параболу. ![]() .
.
![]()
![]()
![]() .
.
Доходимо висновку, що крива другого порядку являє собою або канонічний переріз (еліпс, параболу, гіперболу), або пару прямих (можливо, таких, що збігаються).
Еліпс
Означення. Канонічним рівнянням еліпса називається рівняння
![]() (1)
(1)
Осі координат є осями симетрії еліпса, оскільки рівняння (1) не змінюється в результаті заміни х на –х або у на –у. Початок координат є центром симетрії еліпса. Точки перетину еліпса його осями симетрії називаються вершинами еліпса (рис. 3.43).

Рис. 3.43
1. Увесь еліпс міститься всередині прямокутника ![]() .
.
Справді, із рівняння (1) випливають нерівності:
![]()
2. Форму еліпса можна чітко уявити, довівши, що еліпс утворюється з кола стискуванням вздовж однієї з його осей.
Справді, стиснемо коло
![]()
уздовж осі у заміною змінної:
![]() (2)
(2)
При цьому дістанемо рівняння
![]()
що є рівнянням еліпса:
![]() .
.
Відомо, що в колі діаметр, перпендикулярний до хорди, поділяє її пополам. Окрім того, діаметр, проведений у точку дотику, перпендикулярний до дотичної. При стискуванні кола зберігається така властивість: діаметр еліпса, проведений у точку дотику до нього деякої прямої, поділяє пополам усі хорди, паралельні дотичній. Якщо
![]()
являють рівняння діаметра і хорд, які ділять цим діаметром пополам, то при перетворенні координат (2) дістанемо взаємно перпендикулярні прямі
![]()
Отже, виконується рівність
![]()
 . (3)
. (3)
Діаметр еліпса ![]() , називається спряженим до діаметра
, називається спряженим до діаметра ![]() . Він поділяє пополам усі хорди еліпса, що подаються рівнянням
. Він поділяє пополам усі хорди еліпса, що подаються рівнянням ![]() .
.
Візьмемо на еліпсі довільну точку М0(х0, у0) і проведемо в цій точці дотичну до еліпса. Діаметр, що виходить з точки дотику, має кутовий коефіцієнт ![]() . Тому кутовий коефіцієнт k2 дотичної подається згідно з (3):
. Тому кутовий коефіцієнт k2 дотичної подається згідно з (3):
![]() .
.
Рівняння дотичної набирає вигляду
![]()
або
![]() .
.
|
Остаточно знаходимо рівняння дотичної до еліпса: |
(4) |
|
|
Коли відомі а та b, можемо знайти ексцентриситет еліпса.
Введемо параметр ![]() за формулою
за формулою
![]() (5)
(5)
З рівняння (5) при ![]() знаходимо значення с:
знаходимо значення с:
![]()
Отже,
![]() (6)
(6)
3. Доведемо фокальну властивість еліпса, яку можна також взяти за означення еліпса.
Означення. Еліпсом називається геометричне місце точок, сума відстаней яких до двох фіксованих точок, що називаються фокусами, є величина стала.
Відстань між фокусами дорівнює 2с. Нехай вісь х проходить через фокуси, а вісь у поділяє відрізок між фокусами пополам (рис. 3.44).
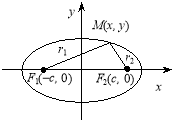
Рис. 3.44
Нехай М(х, у) — довільна точка на еліпсі, причому
![]()
або
![]() (7)
(7)
Звільнимося від ірраціональності в рівнянні
![]()
піднісши обидві його частини до квадрата:
![]()
Звідси маємо:
![]() (8)
(8)
Виконаємо перетворення:
![]()
![]() (9)
(9)
Оскільки ![]() , то рівняння (9) збігається з рівнянням еліпса (1).
, то рівняння (9) збігається з рівнянням еліпса (1).
Рівняння (8) можна записати у вигляді
![]()
4. Прямі, задані рівняннями
![]()
є директрисами еліпса (рис. 3.45).

Рис. 3.45
Справді, з рис. 3.45 знаходимо відстані до директрис:
![]()
Далі визначаємо відношення фокальних радіусів r1, r2 до директрис:
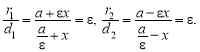
Ці відношення, як бачимо, дорівнюють ексцентриситету ![]() .
.
![]() Знайти канонічне рівняння еліпса, коли відомо, що
Знайти канонічне рівняння еліпса, коли відомо, що ![]() .
.
Маємо рівняння
![]()
з яких визначаємо а = 5. Рівняння еліпса подається так:
![]()
Гіпербола
Означення. Канонічним рівнянням гіперболи називаються рівняння
![]() (1)
(1)
Ця крива розміщена симетрично відносно осей х та у. Початок координат є центром симетрії гіперболи. З рівняння
![]()
випливає, що ![]() .
.
1. Гіпербола утворена двома вітками, які містяться в області
![]() .
.
Справді, з рівняння (1) маємо:
![]() .
.
|
Область, в якій розміщені вітки гіперболи, обмежені прямими |
(2) |
|
|
|
|
які називаються асимптотами гіперболи. |
З рівняння
![]()
бачимо, що узростає зі зростанням х при ![]() (рис. 3.46).
(рис. 3.46).
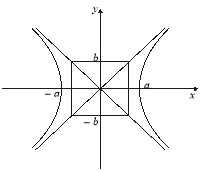
Рис. 3.46
2. Розглянемо вітку гіперболи, яка визначається рівнянням
![]() ,
,
і доведемо, що при ![]() ця вітка наближається до асимптоти з рівнянням
ця вітка наближається до асимптоти з рівнянням ![]() .
.
Справді, маємо такі співвідношення:
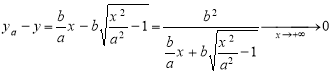 .
.
Багато властивостей гіперболи аналогічні властивостям еліпса.
Означення. Пряма, що проходить через центр симетрії гіперболи, називається її діаметром. Центри всіх хорд гіперболи, що мають рівняння
![]() ,
,
лежать на діаметрі гіперболи, який подається рівнянням ![]()
![]() .
.
Діаметри гіперболи
![]() (3)
(3)
називаються спряженими. Хорди гіперболи, паралельні одному й тому самому діаметру, поділяються спряженим діаметром пополам. Якщо дотична до гіперболи паралельна деякому діаметру, то спряжений діаметр проходить через точку дотику.
Рівняння дотичної до гіперболи в точці М0(х0, у0) подається у вигляді
![]() . (4)
. (4)
3. Знайдемо ексцентриситет гіперболи, скориставшись рівнянням (1). Для цього візьмемо
![]() .
.
Остаточно при ![]() маємо:
маємо:
![]() ,
,
або
![]() (5)
(5)
![]() Знайдемо ексцентриситет гіперболи
Знайдемо ексцентриситет гіперболи
![]() .
.
Маємо: ![]() .
.
4. Доведемо фокальну властивість гіперболи, яка може використовуватися для означення гіперболи.
Означення. Гіперболою називається геометричне місце точок, різниця відстаней яких до двох даних точок, що називаються фокусами, є величина стала.
Відстань між фокусами дорівнює 2с. Проведемо вісь х через фокуси і припустимо, що вісь у поділяє відрізок між фокусами пополам (рис. 3.47).
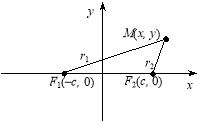
Рис. 3.47
Візьмемо
![]()
або
![]() . (6)
. (6)
Тут знак «+» для правої вітки гіперболи, а знак «–» — для лівої.
Перетворимо це рівняння гіперболи, позбавившись від ірраціональності:
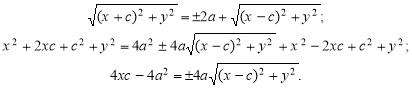
Отже,
![]() (7)
(7)
Звідси:
![]()
Остаточно:
![]()
Роблячи заміну ![]() , дістаємо відоме канонічне рівняння гіперболи.
, дістаємо відоме канонічне рівняння гіперболи.
Рівняння (7) можна подати у вигляді
![]() (8)
(8)
Знак «+» відповідає правій вітці гіперболи, знак «–» — лівій.
5. Доведемо, що прямі ![]() є директрисами гіперболи (рис. 3.48).
є директрисами гіперболи (рис. 3.48).
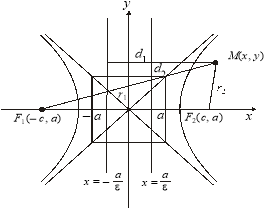
Рис. 3.48
Для довільної точки на правій вітці гіперболи М(х, у) маємо:
![]() .
.
Обчислюємо відношення фокальних радіусів до відстаней директрис:
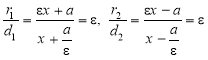 .
.
Ці відношення сталі і дорівнюють ексцентриситету. Це й доводить, що прямі ![]() є директрисами.
є директрисами.
![]() Дано рівняння директрис гіперболи
Дано рівняння директрис гіперболи ![]() , відстані між фокусами якої дорівнюють 10. Записати канонічне рівняння гіперболи.
, відстані між фокусами якої дорівнюють 10. Записати канонічне рівняння гіперболи.
З рівностей ![]() знаходимо
знаходимо ![]()
![]() , а далі записуємо рівняння
, а далі записуємо рівняння ![]() .
.
Парабола
Означення: Канонічним рівнянням параболи називається рівняння виду
![]() (1)
(1)
Ця крива розміщена симетрично відносно осі х, оскільки заміна у на –у в її рівнянні не змінює його. Точка О перетину осі симетрії з параболою називається вершиною параболи (рис. 3.41).
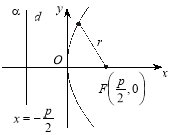
Рис. 3.41
Ексцентристет параболи дорівнює одиниці, а тому ![]() . Важливою є так звана оптична властивість параболи, яка полягає в тому, що всі промені, паралельні осі х, після відбиття параболи потрапляють у її фокус F (рис. 3.42).
. Важливою є так звана оптична властивість параболи, яка полягає в тому, що всі промені, паралельні осі х, після відбиття параболи потрапляють у її фокус F (рис. 3.42).

Рис. 3.42
Візьмемо довільну точку М(х, у) на параболі ![]() і проведемо дотичну в точці М. Кутовий коефіцієнт дотичної визначається так:
і проведемо дотичну в точці М. Кутовий коефіцієнт дотичної визначається так:
![]() .
.
Доведемо, що кут падіння променя на дотичну дорівнює куту його відбиття . Достатньо довести, що
![]() тобто
тобто ![]() або
або ![]() .
.
Згідно з рис. 3.42 маємо:
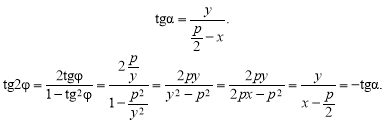
Це й доводить оптичну властивість параболи.
![]() Знайдемо координати фокуса параболи
Знайдемо координати фокуса параболи
![]()
Беручи
![]()
дістанемо рівняння параболи виду (1)
![]()
Оскільки ![]() , то фокус F має координати
, то фокус F має координати ![]() . Отже, знаходимо координати фокуса
. Отже, знаходимо координати фокуса
![]()
Самостійне вивчення №8
Тема: Системи лінійних нерівностей. Основні задачі і поняття лінійного програмування.
Література: Д-5 с. 37-44.
В результаті самостійного вивчення студент повинен
знати:
- основні задачі лінійного програмування;
- основні поняття лінійного програмування;
вміти:
- розв’язувати системи лінійних нерівностей;
- розв’язувати задачі лінійного програмування.
Короткі теоретичні відомості та методичні вказівки
Нерівності. Системи нерівностей
Означення.
|
|
b – a > 0; |
а менше від b; |
|
2) a > b; |
a – b > 0; |
а більше від b; |
|
3) a b; |
b – a > 0 або b – a = 0; |
а менше або дорівнює b; |
|
4) a b; |
a – b > 0 або a – b = 0; |
а більше або дорівнює b. |
Геометрична інтерпретація нерівності а b: число a міститься на числовій осі далі вліво від числа b.
![]() (рис. 1.18).
(рис. 1.18).

Рис. 1.18
Властивості нерівностей:
1) a b i b c a c;
2) a b i c d a + c b + d;
3) a b a + c b + c; a – c b – c;
4) a b; c > 0 ac bc; a/c b/c;
a b; c < 0 ac bc; a/c b/c;
– a – b;
5) ![]()
![]() Розв’язати нерівність:
Розв’язати нерівність:
4 – 3х > 2x + 14.
– 3x – 2x > 14 – 4 за властивістю 3;
– 5x > 10;
– х > 2 : 5;
x < – 2 за властивістю 4.
Відповідь.х х < – 2.
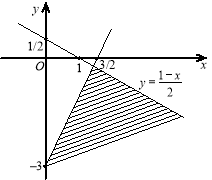
![]() Розв’язати систему нерівностей:
Розв’язати систему нерівностей:
![]()
З першої нерівності системи дістаємо:
![]() .
.
З другої нерівності:
![]() .
.
Зобразимо на площині розв’язки нерівностей (рис. 1.19).
Рис. 1.19
Самостійне вивчення №9
Тема: Означення диференціалу функції. Геометричний та фізичний зміст диференціалу. Правила знаходження диференціалу. Диференціал складеної функції. Застосування диференціалу до наближених обчислень.
Література: О-1 с. 51-54; О-2 с. 204-205; О-4 с. 84-88; О-5 с.245-255; О-6 с. 199-210; Д-5 с. 83-88; Д-6 с. 118-122.
В результаті самостійного вивчення студент повинен
знати:
- означення диференціалу функції, його геометричний та фізичний зміст;
- правила знаходження диференціалу;
вміти:
- знаходити диференціал функції;
- знаходити диференціал складеної функції;
- застосовувати диференціал до наближених обчислень.
Короткі теоретичні відомості та методичні вказівки
Диференціал
Нехай функція у = f(x) диференційовна в інтервалі ![]() .
.
З означення диференційовності маємо:
![]()
Звідси можна записати:
![]() (1)
(1)
де функція ![]() при
при ![]() задовольняє умову
задовольняє умову
![]()
Із (1) для приросту функції дістаємо:
![]()
Покладемо, що ![]() .
.
Означення. Величина f(x)х називається диференціалом функції f(x) за приростом х.
Позначення: ![]()
Геометрична інтерпретація:
Диференціал ![]() є лінійним наближенням (апроксимацією) до приросту функції:
є лінійним наближенням (апроксимацією) до приросту функції: ![]() . Наскільки менше
. Наскільки менше ![]() , настільки краще наближення (апроксимація) (рис. 5.13).
, настільки краще наближення (апроксимація) (рис. 5.13).
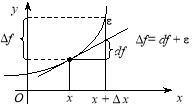
Рис. 5.13
![]() Нехай
Нехай ![]() . Знайдемо диференціал df(x) і приріст f(x) для
. Знайдемо диференціал df(x) і приріст f(x) для ![]() і
і ![]() і порівняємо їх.
і порівняємо їх.
![]()
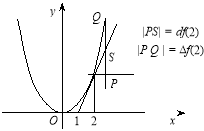
Рис. 5.14
1) ![]() ;
;
![]()
![]()
![]() (рис. 5.14).
(рис. 5.14).
2) ![]()
![]()
![]() .
.
![]()
![]() .
.
Правила обчислення диференціала
Правило 1. Нехай ![]() .
.
Тоді![]()
або
![]()
Правило 2. Дано ![]() .
.
Тоді ![]()
![]()
Правило 3. Маємо ![]() ,
, ![]() .
.
Тоді
![]()
![]()
![]()
![]() . Знайти диференціал
. Знайти диференціал ![]()
![]() за правилом 3 маємо:
за правилом 3 маємо:
![]()
Правило 4. Якщо ![]() ,
, ![]() , то
, то
![]()
Правило 5. Якщо функція ![]() має обернену
має обернену ![]() , то
, то
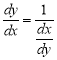 .
.
Правило 6. Якщо функції задані у параметричному вигляді
![]() ,
, ![]() ,
,
то
![]() .
.
![]() Зауваження. Такі перетворення застосовують, виконуючи інтегрування функцій.
Зауваження. Такі перетворення застосовують, виконуючи інтегрування функцій.
Диференціали вищих порядків
Диференціал функції є також функцією незалежної змінної, а тому його можна диференціювати. Розглянемо функцію ![]() .
.
Означення. Другим диференціалом функції у = f(x) називається вираз d(dy).
Позначення:
![]()
Аналогічно дістаємо третій диференціал ![]() і т. д. до диференціала n-го порядку
і т. д. до диференціала n-го порядку ![]() .
.
Диференціал незалежної змінної dx не залежить від х, тому, диференціюючи dx за х, слід розглядати dx як величину сталу відносно х. Отже, приходимо до простих співвідношень між послідовними диференціалами і послідовними похідними:
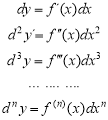 (1)
(1)
![]() Знайти третій диференціал функції
Знайти третій диференціал функції
![]() .
.
Згідно з (1) дістаємо:
![]()
![]()
![]() Зауваження. Формули (1) при
Зауваження. Формули (1) при ![]() будуть неправильними в загальному випадку, якщо змінна х є функцією від незалежного аргументу t. Виняток становитиме випадок, коли х є лінійною функцією незалежного аргументу t і
будуть неправильними в загальному випадку, якщо змінна х є функцією від незалежного аргументу t. Виняток становитиме випадок, коли х є лінійною функцією незалежного аргументу t і ![]() .
.
Справді, при незалежному аргументі х функції f(x) маємо:
![]() .
.
Якщо у функції у = f(x) аргумент х є функцією змінної t, тобто х = (t), то dx вже залежить від t, і dx = (t)dt, тому при x = (t) дістаємо:
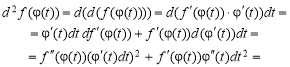 (2)
(2)
![]()
Розглядаючи вирази (1) і (2), доходимо висновку, що форма диференціала другого порядку не зберігається з переходом до складеної функції.
Самостійне вивчення №10
Тема: Зростання та спадання функцій. Стаціонарні та критичні точки. Друга похідна та її фізичний зміст. Опуклість, точки перегину графіка функції. Асимптоти графіка функції. Загальна схема дослідження та побудова графіка функції. Найбільше та найменше значення функції на відрізку. Розв’язування прикладних задач на максимум та мінімум.
Література: О-1 с. 55-68; О-2 с. 220-232; О-4 с. 63-75;
О-5 с. 255-287; О-6 с. 178-198; Д-4 с. 220-261;
Д-6 с.124-142.
В результаті самостійного вивчення студент повинен
знати:
- необхідні та достатні умови існування екстремумів функції;
- необхідні та достатні умови існування проміжків монотонності функції;
- загальну схему дослідження функції;
вміти:
- знаходити проміжки зростання та спадання функції, її екстремуми;
- знаходити точки перегину функції та проміжки опуклості;
- знаходити асимптоти графіка функції;
- досліджувати функції та будувати її графік;
- знаходити найбільше та найменше значення функції на відрізку;
- розв’язувати прикладні задачі на мінімум та максимум.
Короткі теоретичні відомості та методичні вказівки
ДОСЛІДЖЕННЯ ФУНКЦІЙ
Дослідження функцій можна проводити за трьома рівнями.
1-й рівень. Дослідження функції з допомогою елементарних властивостей функції.
2-й рівень. Дослідження функцій за допомогою першої похідної.
3-й рівень. Дослідження функцій за допомогою похідних другого і вищих порядків.
Дослідження функцій за допомогою елементарних властивостей
До елементарних властивостей (характеристик) функції відносимо такі поняття, як область визначення і значень функції, симетричність і парність, непарність, періодичність функції, монотонність.
Твердження, на підставі яких можна встановлювати парність, непарність, періодичність і монотонність функцій, а саме:
а) функція не є парною або непарною, якщо її область визначення не симетрична відносно нуля числової прямої;
б) функція f(x) не є парною або непарною, якщо корені рівняння f(x) = 0 не розміщені симетрично відносно нуля числової прямої;
в) нехай задано функції f(x) і (x). Якщо функція f((x)) визначена на Е, а (x) парна на Е, то і f((x)) парна на Е. Наприклад, функція f(x) = 4cosx парна на R.
г) строго монотонна функція не є періодичною;
д) якщо функції f(x) і (x) одночасно або зростаючі, або спадні, f((x)) і (x) визначені на Е, то f((x)) зростаюча на Е;
е) якщо функція f(x) зростаюча, а (x) спадна або, навпаки, f(x) спадна, (x) зростаюча, f((x)) і (x) визначені на Е, то f((x)) спадна на Е. Наприклад, функція f(x) = 2x зростаюча на R, тому f(x) = 2cosx зростає на тих проміжках із R, де зростає cosx, і спадає там, де спадає cosx.
Ознака сталості диференційовних функцій
Теорема 1. Нехай функція f(x) неперервна на проміжку
[a; b] і диференційовна в кожній його внутрішній точці. Для того щоб функція f(x) була сталою на проміжку [a; b], необхідно і достатньо, аби ![]() для всіх
для всіх ![]() .
.
Доведення. Необхідність. Оскільки за умовою ![]() ,
, ![]() , то
, то ![]() для всіх
для всіх ![]() .
.
Достатність. Нехай тепер f(x) неперервна на проміжку [a; b] і ![]() для
для ![]() . Зафіксуємо точку
. Зафіксуємо точку ![]() . Візьмемо довільну точку
. Візьмемо довільну точку ![]() ,
, ![]() і застосуємо теорему Лагранжа до функції f(x) на проміжку [х0; х], якщо х0 < x або на проміжку [х; х0], якщо х < x0. В обох випадках
і застосуємо теорему Лагранжа до функції f(x) на проміжку [х0; х], якщо х0 < x або на проміжку [х; х0], якщо х < x0. В обох випадках
![]() ,
,
де с лежить між х0 і х. Оскільки ![]() , то
, то ![]() і, отже,
і, отже, ![]() , або
, або ![]() для х[a; b], тобто f(x) — стала функція, яка дорівнює f(x0) на проміжку [a; b].
для х[a; b], тобто f(x) — стала функція, яка дорівнює f(x0) на проміжку [a; b].
Зростання і спадання функціїв точці і на проміжку
Означення. Нехай функція f(x) визначена на проміжку (a; b) і х0(a; b). Кажуть, що f(x) зростає в точці x0, якщо існує окіл точки x0, в якому f(x) < f(x0) для х < x0, а для х > x0
f(x) > f(x0).
Аналогічно за означенням f(x) спадає в точці х0(a; b), якщо існує її окіл, в якому f(x) > f(x0) для х < x0, а f(x) < f(x0) для х > x0.
Теорема 2 (достатня ознака зростання і спадання функції в точці). Якщо функція f(x) диференційовна в точці х0(a; b) і f(x0) > 0 (f(x0) < 0), то f(x) зростає (спадає) в точці х0.
Доведення. Проведемо доведення для випадку, коли f (x0) > 0. Оскільки ![]() , то існує окіл точки х0, в якому
, то існує окіл точки х0, в якому ![]() для х х0. Звідси випливає, що в цьому околі f(x) < f(x0) для х < x0, тобто f(x) зростає в точці x0. Аналогічно доводиться випадок, коли f(x0) < 0.
для х х0. Звідси випливає, що в цьому околі f(x) < f(x0) для х < x0, тобто f(x) зростає в точці x0. Аналогічно доводиться випадок, коли f(x0) < 0.
Теорема 3 (достатня ознака зростання і спадання функції на проміжку). Якщо функція f(x) зростає (спадає) в кожній точці інтервалу (a; b), то вона (спадає) на цьому інтервалі.
5.6.4. Ознаки монотонності диференційовних функцій
Розглянемо деякі ознаки монотонності і строгої монотонності диференційовних на проміжку функцій.
Теорема 4 (ознака монотонності). Нехай функція f(x) неперервна на проміжку [а; b] і диференційовна в інтервалі (a; b). Тоді:
1) для того щоб функція f(x) була монотонно зростаючою на проміжку [а; b], необхідно і достатньо, аби виконувалася нерівність ![]() для всіх х(a; b);
для всіх х(a; b);
2) для того щоб функція f(x) була монотонно спадною на проміжку [а; b], необхідно і достатньо, аби виконувалась нерівність ![]() для всіх х(a; b).
для всіх х(a; b).
Доведення. Проведемо доведення першого пункту теореми.
Необхідність. Нехай функція f(x) неперервна і неспадна на [а; b] і має скінченну похідну f(x) в інтервалі (a; b). Покажемо, що f (x) 0 для х(a; b). За умовою для будь-якого х(a; b) існує ![]() . Крім того, для
. Крім того, для ![]() із (a; b) f(t) f(x) і, отже, для t > х
із (a; b) f(t) f(x) і, отже, для t > х
![]() ,
,
тому
![]() ,
,
що і доводить необхідність.
Достатність. Нехай функція f(x) неперервна на проміжку [а; b] і ![]() для будь-яких х(a; b). Задамо довільні х2 і х1 із [а; b] за умови х2 > х1. За теоремою Лагранжа
для будь-яких х(a; b). Задамо довільні х2 і х1 із [а; b] за умови х2 > х1. За теоремою Лагранжа ![]() , звідки
, звідки ![]() .
.
Отже, для х1 і х2 із (а; b) при х2 > х1 дістаємо f(x2) f(x1), тобто функція f(x) зростає.
Теорема 5 (ознака строгої монотонності). Нехай функція f(x) неперервна на проміжку [а; b] і диференційовна в інтервалі (a; b). Для того щоб функція f(x) була зростаючою (спадною) на проміжку [а; b], необхідно і достатньо виконання двох умов:
1) f(x) 0 (f(x) 0) для будь-якого х(a; b);
2) рівність f(x) = 0 не повинна виконуватися в жодному інтервалі, що лежить в [а; b].
Теорема 6 (достатня ознака строгої монотонності). Нехай функція f(x) неперервна на проміжку [а; b] і диференційовна в інтервалі (a; b). Якщо f(x) > 0 для всіх х(a; b), то f(x) зростає на [а; b], якщо ж f(x) < 0 для всіх х(a; b), то f(x) спадає на [а; b].
Дослідження диференційовної функції на монотонність
1. Знайти нулі функції f (x), тобто корені рівняння f (x) = 0 (якщо вони є), і розбити інтервал (a; b) за допомогою знайдених коренів х1, х2, …, хk, a < x1 < x2 < … < xk < b, на інтервалі (а; х1), (х1; х2), …, (хk–1; хk), (хk; b).
2. Визначити знак похідної на кожному із таких інтервалів. Якщо при цьому виявиться, що на двох сусідніх інтервалах ![]()
![]() похідна f (x) має один і той самий знак, то функція строго монотонна в інтервалі
похідна f (x) має один і той самий знак, то функція строго монотонна в інтервалі ![]() ;
;![]() . Наприклад, якщо f (x) > 0, то функція f(x) зростаюча, якщо f (x) < 0, то f(x) спадна.
. Наприклад, якщо f (x) > 0, то функція f(x) зростаюча, якщо f (x) < 0, то f(x) спадна.
Строга монотонність за теоремою 6 зберігається, якщо до частинного інтервалу приєднати його кінці, на яких за умовою функція неперервна. Якщо f(x) на проміжку [а; b] неперервна, а в інтервалі (a; b) похідна f (x) не перетворюється на нуль, то на проміжку [а; b] функція f(x) буде строго монотонною, а саме при f (x) > 0 — зростаючою, при f (x) < 0 — спадною.
![]() Знайти інтервали зростання і спадання функції
Знайти інтервали зростання і спадання функції
![]() .
.
● Маємо
![]() ,
,
звідки
Похідна f (x) неперервна для х(– ; + ) і перетворюється на нуль лише в точках х = 0, х = 1, х =3, тому вона в інтервалах (– ; 0), (0; 1), (1; 3) і (3; + ) зберігає знак. Оскільки f(– 1) > 0, ![]() , f (2) < 0,
, f (2) < 0,
f (5) > 0, f (х) > 0, якщо х(– ; 0), f (х) > 0, х(0; 1), f (х) < 0, х(1; 3), f (х) > 0, х(3; + ).
Тому функція f(x) зростає на інтервалах (– ; 0); (0; 1); (3; + ) і спадає на інтервалі (1; 3).
Поняття максимуму та мінімуму на множині
Нехай функція f(x) визначена на числовій множині Е.
Означення. Функція f(x) на множині Е має найбільше значення В або максимум (найменше значення А або мінімум), коли існує точка х0Е така, що для всіх хЕ виконується умова
![]()
Позначатимемо:
Максимум (мінімум) функції на множині інколи називають абсолютним максимумом (абсолютним мінімумом).
Можна помітити, що коли ![]() , то
, то ![]() . Також
. Також ![]() , коли
, коли ![]() . Отже, коли функція f(x) на множині Е має максимум (мінімум), то цей максимум (мінімум) збігається з верхньою (нижньою) межею значень функції на множині Е.
. Отже, коли функція f(x) на множині Е має максимум (мінімум), то цей максимум (мінімум) збігається з верхньою (нижньою) межею значень функції на множині Е.
Зауважимо, що функція на заданій множині може і не мати максимуму або мінімуму.
![]() Знайти найбільше і найменше значення функції:
Знайти найбільше і найменше значення функції:
f(x) = х2, хЕ = {– 1, 0, 1, 2, 3}.
● Маємо ![]() f(x) = f(3) = 9,
f(x) = f(3) = 9, ![]() .
.
Поняття максимуму і мінімуму функції в точці (локальний екстремум)
Нехай функція f(x) визначена на проміжку [а; b] і х0 — внутрішня точка проміжку: х0(a; b).
Означення. Функція f(x) в точці х0 має максимум, якщо існує окіл точки х0, що для всіх х, х х0, цього околу виконується нерівність f(x) f(x0). Саме значення f(x0) називатимемо максимумом (локальним максимумом) функції f(x) в точці x0 і позначатимемо maxf(x) = f(x0).
Функція f(x) в точці х0 має мінімум, якщо існує окіл точки х0, що для всіх х (х х0), які належать цьому околу, буде виконуватись нерівність f(x) f(x0). При цьому саме значення f(x0) називатимемо мінімумом (локальним мінімумом) функції f(x) в точці х0 і позначатимемо minf(x) = f(x0).
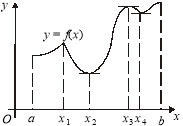
Рис. 5.31
Далі, якщо для х х0 у даному околі точки х0 ![]()
![]() , функція f(x) має строгий максимум (строгий мінімум).
, функція f(x) має строгий максимум (строгий мінімум).
Максимум і мінімум функції в точці об’єднує спільний термін — екстремум (локальний екстремум) функції в точці.
Необхідна умова екстремуму. Стаціонарні і критичні точки функції
Нехай функція f(x) визначена і диференційовна в інтервалі (a; b).
Означення. Точки інтервалу (a; b), в яких похідна f (x) перетворюється в нуль (f (x) = 0), називаються стаціонарними точками функції f(x) в інтервалі (a; b).
Геометрична інтерпретація. Кожна стаціонарна точка х0(a; b) функції f(x), диференційовної в інтервалі (a; b), характеризується тим, що дотична до кривої у = f(x) в точці (х0; f(x0)) паралельна осі абсцис, оскільки кутовий коефіцієнт цієї дотичної ![]() .
.
Нехай функція f(x) неперервна на відрізку [a; b] і диференційовна на проміжку (a; b) за винятком, можливо, скінченного числа точок, в яких функція не має похідної.
Теорема 1. Для того щоб точка х0 була точкою екстремуму функції, визначеної в околі цієї точки, необхідно, щоб похідна функції в цій точці дорівнювала нулю (f(x) = 0) або функція була недиференційовна в цій точці.
Доведення випливає з теореми Ферма.
![]() Означення. Для функції f(x), неперервної на відрізку [а; b] і диференційовної на інтервалі (a; b) (за винятком, можливо, скінченного числа точок, де не існує похідної f(x) в цьому інтервалі), точки, де її похідна дорівнює нулю або не існує, називатимемо критичними її точками на проміжку [а; b], або точками, «підозрілими» на екстремум функції f(x) на проміжку [а; b].
Означення. Для функції f(x), неперервної на відрізку [а; b] і диференційовної на інтервалі (a; b) (за винятком, можливо, скінченного числа точок, де не існує похідної f(x) в цьому інтервалі), точки, де її похідна дорівнює нулю або не існує, називатимемо критичними її точками на проміжку [а; b], або точками, «підозрілими» на екстремум функції f(x) на проміжку [а; b].
Знайти критичні точки функції
![]() .
.
● Маємо f(x) = х2 – 5х + 6. Розв’язавши рівняння f (x) = 0, дістанемо х = 2 і х = 3. Оскільки функція f(x) диференційовна, то критичними точками будуть лише стаціонарні, тобто точки х = 2 і х = 3.
достатні умови строгого екстремуму
Нехай функція f(x) диференційовна в деякому околі точки х0, за винятком, можливо, самої точки х0. Будемо говорити, що похідна f (x) при переході через точку х0 змінює знак із плюса на мінус, якщо існує такий окіл ![]() точки х0, що для
точки х0, що для ![]() f (x) > 0, а для
f (x) > 0, а для ![]() f(x) < 0. Аналогічно f (x) при переході через точку х0 змінює знак із мінуса на плюс, якщо існує окіл
f(x) < 0. Аналогічно f (x) при переході через точку х0 змінює знак із мінуса на плюс, якщо існує окіл ![]() точки х0, що для
точки х0, що для ![]() f (x) < 0, а для
f (x) < 0, а для ![]() f(x) > 0.
f(x) > 0.
Нарешті, f(x) при переході через точку х0 не змінює знака, якщо для ![]() і для
і для ![]() f(x) зберігає один і той самий знак (буде або додатна, або від’ємна).
f(x) зберігає один і той самий знак (буде або додатна, або від’ємна).
Теорема 2. Нехай функція f(x) диференційовна в околі точки х0, за винятком, можливо, самої точки х0, в якій f(x) неперервна. Тоді:
1) якщо при переході через точку х0 похідна f (x) змінює знак з плюса на мінус, то в точці х0 функція f(x) має строгий максимум;
2) якщо при переході через точку х0 похідна f (x) змінює знак з мінуса на плюс, то в точці х0 функція f(x) має строгий мінімум;
3) якщо при переході через точку х0 похідна f (x) не змінює знака, то в точці х0 функція f(x) екстремуму не має.
![]() Дослідити на екстремум функцію
Дослідити на екстремум функцію
f(x) = 2х3 – 15х2 + 36х – 20.
Маємо
![]() .
.
Із рівняння f(x) = 0 знаходимо дві стаціонарні точки: х = 2 і х = 3. При переході через точку х = 2 похідна f(x) змінює знак з плюса на мінус, отже, за теоремою 2 функція f(x) в точці х = 2 має максимум: max f(x) = f(2) = 8.
Аналогічно знайдемо, що в точці х = 3 функція f(x) має мінімум: min f(x) = f(3) = 7.
Теорема 3. Нехай функція f(x) має похідні до n-го порядку включно в околі х0, причому функція f (n)(x) неперервна в точці х0 і f(x0) = f(x0) = … = f (n–1)(x0) = 0, але f (n)(x0) 0. Тоді:
1) якщо n парне (n 2), то функція f(x) в точці x0 має строгий екстремум, причому мінімум — при f (n)(x0) > 0 і максимум — при f (n)(x0) < 0;
2) якщо n непарне, то функція f(x) в точці x0 екстремуму не має.
![]() Дослідити на екстремум функцію
Дослідити на екстремум функцію
f(x) = х3 – 3х2 + 3х +5.
Знаходимо похідну f (x) = 3х2 – 6х + 3. Рівняння f (x) = 0 має одну стаціонарну точку х = 1, тому f (1) = 0. Далі,
![]() .
.
Отже, f (1) = f (1) = 0, але f (1) 0. За теоремою в стаціонарній точці х = 1 функція f(x) екстремуму не має.
Теорема 4. Нехай функція f(x) диференційовна в околі стаціонарної точки х0, а в самій стаціонарній точці має похідну другого порядку. Тоді:
1) якщо f (х0) > 0, то функція f(x) в точці х0 має мінімум;
2) якщо f (х0) < 0, то функція f(x) в точці х0 має максимум;
3) якщо f (х0) = 0, то в точці х0 може бути екстремум, а може і не бути.
Доведення. Нехай f (х0) > 0, тоді, ураховуючи, що х0 — стаціонарна точка (f(х0) = 0), дістаємо
![]() .
.
Оскільки границя виразу ![]() в точці х0 додатна, то існує окіл точки х0, що для всіх x < x0 f(x) < 0, а для x> x0 f(x) > 0 із вказаного околу. У точці х0 функція f(x) неперервна, тому за теоремою 2 в точці х0 функція має мінімум.
в точці х0 додатна, то існує окіл точки х0, що для всіх x < x0 f(x) < 0, а для x> x0 f(x) > 0 із вказаного околу. У точці х0 функція f(x) неперервна, тому за теоремою 2 в точці х0 функція має мінімум.
Аналогічно доводиться теорема про максимум функції f(x) в точці х0, якщо f (х0) < 0.
![]() Дослідити на екстремум функцію f(x) = х6.
Дослідити на екстремум функцію f(x) = х6.
Маємо f (x) = 6х5. Стаціонарна точка одна: х = 0.
1) За теоремою 2 при переході через стаціонарну точку х = 0 похідна f (x) змінює знак з мінуса на плюс. Отже, у точці х = 0 функція f(x) має строгий мінімум.
2) За теоремою 3 маємо f (х) = 30х4, f (х) = 120х3, f (4)(x) = 360х2, f (5)(x) = 720х, f (6)(x) = 720, причому f (0) = f (0) = f (0) = 0, але f (6)(0) = 720 > 0. Оскільки число 6 парне, то за теоремою 3 в точці х = 0 функція f(x) має строгий мінімум.
3) Оскільки f (0) = 0, f (0) = 0, то теорема 4 не дає відповіді про екстремум функції в стаціонарній точці х = 0.
4) Дослідження функції на екстремум можна виконати і без використання диференційовності. Оскільки |х| > 0 для х 0 і |0| = 0, то і х6 = 0 для х = 0, звідки функція f(x) = х6 у точці х = 0 має строгий мінімум.
Цей приклад показує, що при дослідженні функції f(x) на екстремум треба звернути увагу на вид самої функції, щоб обрати найбільш раціональний спосіб розв’язування конкретної задачі.
Найбільше і найменше значення функції на проміжку
(абсолютний екстремум)
1. Знаходження найбільших і найменших значень функції на проміжку. Розглянемо деякі випадки знаходження найбільших і найменших значень функцій на проміжку, коли функція неперервна і диференційовна на всьому проміжку за винятком точок, де в неї немає скінченної похідної.
І. Нехай функція f(x) неперервна на проміжку [a; b], диференційовна в інтервалі (a; b) і має скінченне число стаціонарних точок.
Алгоритм знаходження найбільшого і найменшого значень функції f(x) на проміжку [a; b].
1. Знайти корені рівняння f (x) = 0, х(a; b), тобто стаціонарні точки (якщо вони є).
2. Обчислити значення функції f(x) на кінцях проміжку [a; b] і в усіх стаціонарних точках (не обов’язково виясняти, чи буде в них екстремум).
3. На підставі порівняння всіх знайдених значень функції вибрати найбільше і найменше. Вони є відповідно найбільшим і найменшим значеннями функції f(x) на проміжку [a; b].
![]() Знайти найбільше і найменше значення функції
Знайти найбільше і найменше значення функції
![]() на проміжку [0,01; 100].
на проміжку [0,01; 100].
● У даному випадку похідна ![]() в інтервалі [0,01; 100] має тільки один корінь — х = 0,2. Обчислимо значення функції в стаціонарній точці х = 0,2 і на кінцях проміжку [0,01; 100]:
в інтервалі [0,01; 100] має тільки один корінь — х = 0,2. Обчислимо значення функції в стаціонарній точці х = 0,2 і на кінцях проміжку [0,01; 100]:
![]() .
.
Звідси
![]() .
.
2. Нехай функція f(x) неперервна на проміжку [a; b], диференційовна в інтервалі (a; b) за винятком скінченного числа точок і має скінченне число стаціонарних точок.
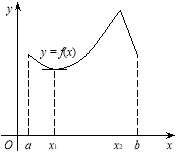
Рис. 5.32
У цьому випадку критичними точками функції f(x) в інтервалі (a; b) будуть не тільки стаціонарні точки, а й точки, в яких не існує похідної (рис. 5.32). Для знаходження найбільшого і найменшого значень функції застосовується алгоритм випадку 1, лише з тією різницею, що потрібно обчислити додатково значення функції в точках, де відсутня похідна.
![]() Знайти найбільше і найменше значення функції
Знайти найбільше і найменше значення функції
![]() на проміжку [0; 2].
на проміжку [0; 2].
Після знаходження похідної функції і розв’язання рівняння f(x) = 0 матимемо, що критичною точкою буде тільки точка х = 1. Знаходимо значення функції f(x) на кінцях проміжку і в критичній точці:
![]()
Звідси
![]() .
.
3. Функція f(x) неперервна — диференційовна в інтервалі (a; b) за винятком, можливо, скінченного числа точок і має скінченне число стаціонарних точок.
У цьому випадку функція f(x) може не мати найбільшого або найменшого значення на проміжку [a; b]. Наприклад, функція f(x) = х2 в інтервалі (0; 1) не має ні найбільшого, ні найменшого значення; функція f(x) = sinx в інтервалі (– ; + ) має найбільше значення, що дорівнює 1, і найменше значення, що дорівнює – 1; функція f(x) = (х – 12)2 + 30 в інтервалі (– ; + ) не має найбільшого значення, але має найменше значення, що дорівнює 30; функція f(x) = 5х2 на проміжку (0; 1] не має найменшого значення, але має найбільше значення, що дорівнює 5.
Дослідження функції f(x), що задовольняє умовам 3 на проміжку [a; b], на найбільше і найменше значення можна виконати так, як і у випадку 2 для проміжку [a; b], з тією лише різницею, що коли немає f(а), то його замінюють граничним значенням ![]() , а коли немає f(b), то його також замінюють граничним значенням
, а коли немає f(b), то його також замінюють граничним значенням ![]() . Потім з порівняння значень функції f(x), як у випадку 2, включаючи граничні значення А (якщо немає f(а)) і В (якщо немає f(b)), найбільшим значенням виявиться граничне, то воно і буде найбільшим значенням функції f(x) на проміжку [a; b].
. Потім з порівняння значень функції f(x), як у випадку 2, включаючи граничні значення А (якщо немає f(а)) і В (якщо немає f(b)), найбільшим значенням виявиться граничне, то воно і буде найбільшим значенням функції f(x) на проміжку [a; b].
Якщо найбільшим значенням функції виявиться граничне, то f(x) на проміжку [a; b] не має найбільшого значення. Аналогічно досліджується питання про найменше значення f(x) на проміжку [a; b].
![]() Знайти найбільше і найменше значення функції
Знайти найбільше і найменше значення функції ![]() в інтервалі (0; 2).
в інтервалі (0; 2).
Оскільки f(1) = 0, ![]() ,
, ![]() , то найбільшим із цих значень буде
, то найбільшим із цих значень буде ![]() , яке є граничним, отже, функція не має найбільшого значення в інтервалі (0; 2). Найменшим значенням буде f(1) = 0, отже, f(1) = 0 є найменшим значенням функції f(x) в інтервалі (0; 2).
, яке є граничним, отже, функція не має найбільшого значення в інтервалі (0; 2). Найменшим значенням буде f(1) = 0, отже, f(1) = 0 є найменшим значенням функції f(x) в інтервалі (0; 2).
Загальний план дослідження
функції і побудова графіків
Побудова графіка функції на основі результатів
І-го рівня дослідження функції
Зауваження. Із школи відомий спосіб побудови графіка функції «за точками». Він випливає із означення графіка функції і є громіздким та недостатньо надійним способом. Розглянемо ефективніший.
![]() 1. Побудувати графік функції
1. Побудувати графік функції ![]() .
.
Для побудови графіка функції дослідимо її, дотримуючись загального алгоритму:
1. Знаходимо область визначення:
![]() ,
, ![]() .
.
2. Визначаємо парність або непарність.
![]() .
.
Функція ![]() — парна. Подальше дослідження будемо вести для
— парна. Подальше дослідження будемо вести для ![]() .
.
3. Визначаємо проміжки монотонності.
![]() .
.
При зростанні значень х від 1 до значення y зростають.
4. Знаходимо корені функції та проміжки знакосталості.
Якщо ![]() , то
, то ![]() при
при ![]() .
.
![]() при всіх
при всіх ![]() .
.
5. Встановлюємо області зміни функції.
Якщо ![]() , то
, то ![]() . Якщо
. Якщо ![]() , то
, то ![]() . Отже,
. Отже, ![]() .
.
6. Досліджуємо на опуклість та вгнутість
Легко доводиться нерівність.
![]() , 1 ≤ х1 < x2.
, 1 ≤ х1 < x2.
Графік функції — опукла крива.
7. Будуємо графік функції (рис. 5.33).
Рис. 5.33
Асимптоти кривої
Означення. Асимптотою кривої називають пряму (або криву) лінію, до якої необмежено наближається точка, рухаючись по кривій у нескінченність.

Рис. 5.45
1. Вертикальні асимптоти. Нехай функція ![]() визначена в одному з інтервалів (а; с) та (с; b), або на обох із них, причому
визначена в одному з інтервалів (а; с) та (с; b), або на обох із них, причому
с — скінченне число.
Означення. Якщо функція ![]() має в точці с розрив другого роду і існує хоча б одна із нескінченних односторонніх границь функції
має в точці с розрив другого роду і існує хоча б одна із нескінченних односторонніх границь функції ![]() в точці с (наприклад,
в точці с (наприклад, ![]() або
або ![]() , рис. 5.45), то пряму х = с називають вертикальною асимптотою кривої
, рис. 5.45), то пряму х = с називають вертикальною асимптотою кривої ![]() .
.
Отже, усі вертикальні асимптоти виду х = с кривої ![]() можна знайти, знайшовши скінченне число точок с, в яких функція
можна знайти, знайшовши скінченне число точок с, в яких функція ![]() має розриви другого роду й існує хоча б одна із нескінченних односторонніх границь функції f(x) у точці с.
має розриви другого роду й існує хоча б одна із нескінченних односторонніх границь функції f(x) у точці с.
![]() Функція
Функція ![]() має вертикальну асимптоту
має вертикальну асимптоту ![]() (рис. 5.46), оскільки точка
(рис. 5.46), оскільки точка ![]() — точка розриву другого роду:
— точка розриву другого роду:
![]() ;
; ![]() .
.
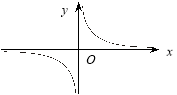
Рис. 5.46
![]() Графік функції
Графік функції ![]() має вертикальні асимптоти
має вертикальні асимптоти ![]() (рис. 5.47).
(рис. 5.47).
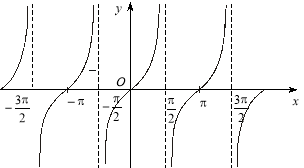
Рис. 5.47
2. Похилі асимптоти.
Означення. Нехай функція ![]() визначена в інтервалі
визначена в інтервалі ![]() або в інтервалі
або в інтервалі ![]() . Пряму
. Пряму ![]() називатимемо асимптотою кривої
називатимемо асимптотою кривої ![]() , якщо виконується умова
, якщо виконується умова
![]() .
.
Геометрична ілюстрація (рис. 5.48). Різниця ординат кривої ![]() і прямої
і прямої ![]() прямує до нуля, коли їх абсциси прямують до нескінченності:
прямує до нуля, коли їх абсциси прямують до нескінченності: ![]() .
.
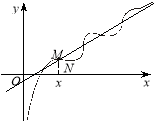
Рис. 5.48
Теорема. Крива ![]() ,
, ![]() тоді і тільки тоді має асимптоту
тоді і тільки тоді має асимптоту ![]() , коли існують скінченні границі
, коли існують скінченні границі
![]() ,
, ![]() . (1)
. (1)
Доведення. Необхідність. Нехай пряма ![]() є асимптотою кривої
є асимптотою кривої ![]() , тобто виконується умова
, тобто виконується умова
![]() .
.
Тоді
![]() .
.
Це можливо лише у випадку:
![]() ,
,
звідки
![]() ,
,
причому ![]() — скінченне за умовою, оскільки пряму
— скінченне за умовою, оскільки пряму ![]() задано. Далі за умовою
задано. Далі за умовою ![]() знаходимо
знаходимо ![]() ,
, ![]() , причому
, причому ![]() — скінченне.
— скінченне.
Достатність. Нехай тепер виконується умова (1), де k і b — скінченні границі, тоді ![]()
![]() , тобто за означенням
, тобто за означенням ![]() — асимптота кривої
— асимптота кривої ![]() .
.
Доведення теореми у випадку, коли ![]() , здійснюється аналогічно, потрібно лише замінити
, здійснюється аналогічно, потрібно лише замінити ![]() на
на ![]() .
.
![]() Знайти асимптоти функції
Знайти асимптоти функції ![]() .
.
У точці ![]() функція має розрив другого роду, тому
функція має розрив другого роду, тому ![]() — вертикальна асимптота. Знайдемо похилу асимптоту. За теоремою
— вертикальна асимптота. Знайдемо похилу асимптоту. За теоремою
![]() ,
, ![]() .
.
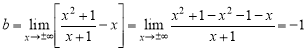 ,
, ![]() .
.
Отже, пряма ![]() є асимптотою функції при
є асимптотою функції при ![]() (рис. 5.49).
(рис. 5.49).

Рис. 5.49
![]() Чи має функція
Чи має функція ![]() похилі асимптоти?
похилі асимптоти?
Функція ![]() похилих асимптот не має, оскільки не існує границі
похилих асимптот не має, оскільки не існує границі ![]() .
.
![]() Знайти похилі асимптоти кривої
Знайти похилі асимптоти кривої ![]() .
.
Областю визначення кривої є частина площини, де ![]() . Застосовуючи теорему про побудову асимптот, дістаємо
. Застосовуючи теорему про побудову асимптот, дістаємо
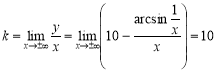 ,
,
![]() .
.
Отже, пряма ![]() є асимптотою кривої при
є асимптотою кривої при ![]() .
.
3. Горизонтальні асимптоти. Якщо в похилій асимптоті ![]() функції
функції ![]() маємо
маємо ![]() , то таку похилу асимптоту називають горизонтальною асимптотою функції. Отже, горизонтальна асимптота — частинний випадок похилої — відшукується як похила асимптота за умов
, то таку похилу асимптоту називають горизонтальною асимптотою функції. Отже, горизонтальна асимптота — частинний випадок похилої — відшукується як похила асимптота за умов
![]() ,
, ![]()
і має вигляд ![]() . До речі, умову
. До речі, умову ![]() можна не перевіряти, якщо
можна не перевіряти, якщо ![]() — скінченна границя, оскільки в такому разі границя
— скінченна границя, оскільки в такому разі границя ![]() завжди дорівнює нулю. Звідси можемо зробити висновок.
завжди дорівнює нулю. Звідси можемо зробити висновок.
Для того щоб пряма ![]() була горизонтальною асимптотою функції
була горизонтальною асимптотою функції ![]() ,
, ![]() ,
, ![]() , необхідно і достатньо, щоб існувала скінченна границя
, необхідно і достатньо, щоб існувала скінченна границя ![]() .
.
![]() Знайти горизонтальні асимптоти функції
Знайти горизонтальні асимптоти функції ![]() .
.
Маємо
![]() ,
, ![]() .
.
Отже, ![]() горизонтальні асимптоти (5.50).
горизонтальні асимптоти (5.50).
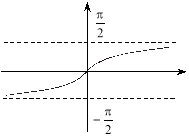
Рис. 5.50
Загальний план дослідження функції
1. Знайти область визначення та значення функції, заданої формулою, якщо таку область не зазначено.
2. Дослідити функцію на парність, непарність, періодичність.
3. З’ясувати точки перетину функції з осями координат.
4. Дослідити функцію на неперервність.
5. Знайти асимптоти графіка функції (якщо вони існують).
6. З’ясувати, як функція поводиться на кінцях кожного з проміжків області визначення (знайти границі функції на кінцях цих проміжків, якщо вони є).
7. Дослідити функцію на диференційовність.
8. Дослідити функцію на монотонність та екстремуми. Знайти екстремуми і значення функції в точках екстремуму.
9. Дослідити функцію на опуклість (вгнутість): знайти інтервали опуклості (вгнутості), а також точки перегину функції.
10. Знайти найбільше і найменше значення функції (якщо вони існують).
11. Побудувати графік функції.
![]() Побудуємо графік функції
Побудуємо графік функції ![]() .
.
1. Функція не існує в точках ![]() . Тому область визначення функції
. Тому область визначення функції
![]()
2. Функція непарна, оскільки ![]() . З огляду на непарність функції достатньо побудувати її графік лише при
. З огляду на непарність функції достатньо побудувати її графік лише при ![]() .
.
Функція неперіодична.
3. Точки перетину з осями координат:
з віссю Ох: ![]()
(0; 0) — точка перетину з віссю Ох.
з віссю Оу: ![]()
(0; 0) — точка перетину з віссю Оу.
4. Функція невизначена в точці ![]() тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці
тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці ![]() :
:
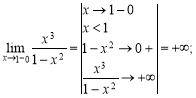
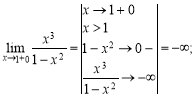
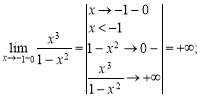
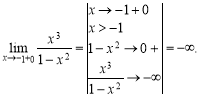
Точки ![]() — точки розриву другого роду.
— точки розриву другого роду.
![]() — область неперервності функції.
— область неперервності функції.
5. Знаходимо асимптоти функції. Насамперед з’ясовуємо, що прямі ![]() — вертикальні асимптоти. (Це випливає з означення вертикальних асимптот та п. 4.)
— вертикальні асимптоти. (Це випливає з означення вертикальних асимптот та п. 4.)
Шукаємо похилу асимптоту ![]()
![]() ;
;
![]() .
.
Отже, ![]() — похила асимптота.
— похила асимптота.
6. В п. 4 знайдені односторонні границі функції в точках ![]() . Залишилось знайти границі функції, коли
. Залишилось знайти границі функції, коли ![]() і
і ![]()
![]()
![]()
7. Знайдемо першу похідну від функції у (вона існує на D (x)):
![]()
8. Дослідимо функцію на монотонність і знайдемо точки екстремуму. Для знаходження стаціонарних точок прирівнюємо першу похідну до нуля:
![]()
![]()
![]()
![]()
Зважаючи на зауваження п. 2, розглядатимемо дослідження функції при ![]()
![]()
![]() , коли
, коли ![]() ,
,
![]() , коли
, коли ![]()
Тому ![]() — точка максимуму,
— точка максимуму, ![]() — точка мінімуму.
— точка мінімуму.
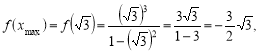
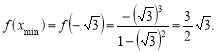
9. Знайдемо другу похідну функції у:
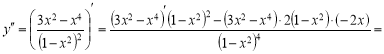
![]()
![]()
Точка х = 0 може бути точкою перегину, бо ![]() Перевіримо це за критерієм. Визначимо знак
Перевіримо це за критерієм. Визначимо знак ![]() в околі точки х = 0
в околі точки х = 0
![]()
Друга похідна змінює в точці х = 0 свій знак, тому функція ![]() має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.
має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.
10. Найбільше та найменше значення функції не існують.
11. Побудуємо графік функції, враховуючи дослідження.
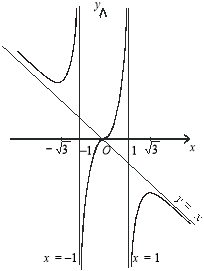
Самостійне вивчення №11
Тема: Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. необхідна умова існування точок екстремуму. Повний диференціал. Частинні похідні вищих порядків. Похідна за напрямом. Градієнт. Умовний екстремум. Метод множників Лагранжа.
Література: О-1 с. 103-112; О-2 с.239-258; Д-6 с. 187-209.
В результаті самостійного вивчення студент повинен
знати:
- означення та приклади функцій багатьох змінних
вміти:
- знаходити область визначення функції двох змінних;
- знаходити частинні похідні та повний диференціал функції двох змінних;
- знаходити похідну за напрямом та градієнт;
- знаходити умовний екстремум функції багатьох змінних.
Короткі теоретичні відомості та методичні вказівки
Частинні похідні та повний диференціал функції n-змінних
Означення. Якщо існує скінченна границя
![]() ,
,
то її називають частинною похідною функції f у точці ![]() за змінною
за змінною ![]() і позначають
і позначають ![]() або
або ![]() .
.
Похідні ![]() ,
, ![]() називають похідними першого порядку.
називають похідними першого порядку.
Правило знаходження частинних похідних першого порядку
Для обчислення частинної похідної ![]() звичайно користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім хk, сталими.
звичайно користуються відомими формулами і правилами диференціювання функції однієї змінної, вважаючи всі змінні, крім хk, сталими.
![]()
Знайти частинні похідні функції
![]() .
.
● Функція визначена в області ![]() Вважаючи, що у стале, знаходимо
Вважаючи, що у стале, знаходимо
![]()
Вважаючи, що х стале, знаходимо
![]()
![]() Знайти частинні похідні функції
Знайти частинні похідні функції
![]()
● Вважаючи, що ![]() ,
, ![]() , знаходимо
, знаходимо
![]()
Вважаючи, що ![]() ,
, ![]() , знаходимо
, знаходимо
![]()
Вважаючи, що ![]() ,
, ![]() , знаходимо
, знаходимо
![]()
Геометрична інтерпретація частинних похідних

Рис. 1.21
Проведемо площину EFGH через точку ![]() даної поверхні паралельно площині y0z. Рівняння цієї площини
даної поверхні паралельно площині y0z. Рівняння цієї площини
х = а.
Отже, рівняння кривої, утвореної в перерізі JPK, буде
![]() ,
,
якщо EF розглядати як вісь z, а EH — як вісь y. У цій площині ![]() означає те саме, що
означає те саме, що ![]() , а тому
, а тому ![]()
Отже, частинна похідна ![]() дорівнює тангенсу кута нахилу до осі y, дотичної до перерізу JК у точці Р.
дорівнює тангенсу кута нахилу до осі y, дотичної до перерізу JК у точці Р.
Аналогічно, якщо провести площину BCD через Р паралельно площині x0z, її рівняння буде
![]() ,
,
і в площині перерізу DPI частинна похідна ![]() означатиме те саме, що й
означатиме те саме, що й ![]() . Звідси
. Звідси ![]()
Отже, частинна похідна ![]() дорівнює тангенсу кута нахилу до осі х, дотичної до перерізу DJ в точці Р.
дорівнює тангенсу кута нахилу до осі х, дотичної до перерізу DJ в точці Р.
Для повного диференціала формула (2) узагальнюється на випадок диференційовної функції n змінних ![]() :
:
![]() (4)
(4)
![]() Знайти
Знайти ![]() якщо
якщо ![]() .
.
● Знайдемо спочатку ![]() ,
, ![]() ,
, ![]() :
:
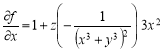 ;
;
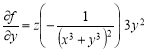 ;
;
![]() .
.
Звідси за формулою (4) дістанемо:
![]()
Властивості повного диференціала
Для будь-яких диференційовних функцій ![]() ,
, ![]() справджуються рівності:
справджуються рівності:
![]() , де , — сталі; (5)
, де , — сталі; (5)
![]() ;
;
![]() ,
, ![]() .
.
Властивість інваріантності форми повного диференціала: Формула (4) виконується не лише тоді, коли х та у — неза-
лежні змінні, а й тоді, коли х і у є диференційовними функціями будь-яких змінних.
Достатня умова диференційовності функції двох змінних у точці
Для функції однієї змінної диференційовність та існування похідної є рівносильними твердженнями. У разі функції багатьох змінних маємо інше: існування частинних похідних — необхідна, але не достатня умова диференційовності функції в точці. Наприклад, для функції
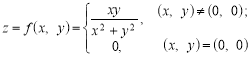
у точці ![]() маємо:
маємо: ![]() ,
, ![]() . Проте ця функція розривна в точці
. Проте ця функція розривна в точці ![]() , а тому вона не може бути диференційовною в цій точці. Отже, для диференційовності функції
, а тому вона не може бути диференційовною в цій точці. Отже, для диференційовності функції ![]() у точці
у точці ![]() не достатньо самого лише існування частинних похідних. Для диференційовності доводиться додатково вимагати неперервності частинних похідних, як це випливає з поданої далі теореми.
не достатньо самого лише існування частинних похідних. Для диференційовності доводиться додатково вимагати неперервності частинних похідних, як це випливає з поданої далі теореми.
Теорема 1.16. Якщо функція ![]() у деякому околі точки
у деякому околі точки ![]() має неперервні частинні похідні, то вона диференційовна в цій точці.
має неперервні частинні похідні, то вона диференційовна в цій точці.
Доведення. Розглянемо в координатній площині х0у точки ![]() ,
, ![]() і
і ![]() (рис. 1.22).
(рис. 1.22).
Нехай частинні похідні визначені в деякому -околі точки Р і точка R належить даному околу. Оскільки -окіл точки Р — це круг радіусом із центром у точці Р, то відрізки PQ i QR цілком належать цьому околу. Отже, функція ![]() визначена на відрізках PQ i QR.
визначена на відрізках PQ i QR.
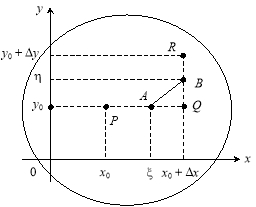
Рис. 1.22
Подамо повний приріст функції ![]() у точці
у точці ![]() у вигляді
у вигляді
![]() (5)
(5)
На відрізку PQ змінна у має стале значення ![]() , тому функція
, тому функція ![]() на цьому відрізку є функцією однієї змінної х. Застосовуючи формулу Лагранжа про середнє значення, дістаємо:
на цьому відрізку є функцією однієї змінної х. Застосовуючи формулу Лагранжа про середнє значення, дістаємо:
![]() (6)
(6)
для деякого значення з інтервалу ![]() . Аналогічно, на відрізку QR функція
. Аналогічно, на відрізку QR функція ![]() залежить лише від у. Тому на проміжку
залежить лише від у. Тому на проміжку ![]() знайдеться точка , для якої
знайдеться точка , для якої
![]() . (7)
. (7)
Згідно з (6) і (7) запишемо формулу (5) у вигляді:
![]() .
.
Звідси
де ![]() ,
, ![]() .
.
Очевидно, що при ![]() і
і ![]() точки А і В прямують до точки Р. Частинні похідні неперервні, тому
точки А і В прямують до точки Р. Частинні похідні неперервні, тому ![]()
![]() коли
коли ![]()
![]()
Разом з та прямує до нуля і величина
![]() .
.
Тому з рівності
![]()
випливає диференційовність функції ![]() у точці
у точці ![]() .
.
Похідна за напрямом. Градієнт
Означення. Нехай функція ![]() визначена в деякому околі точки
визначена в деякому околі точки ![]() ; l — деякий промінь з початком у точці
; l — деякий промінь з початком у точці ![]() ;
; ![]() — точка на цьому промені, яка належить околу точки
— точка на цьому промені, яка належить околу точки ![]() (рис. 1.23);
(рис. 1.23); ![]() — довжина відрізка
— довжина відрізка ![]() . Якщо існує
. Якщо існує ![]() , то ця границя називається похідною функції
, то ця границя називається похідною функції ![]() за напрямом l у точці
за напрямом l у точці ![]() і позначається
і позначається ![]() .
.
Зокрема, ![]() — похідна функції
— похідна функції ![]() за додатним напрямом осі х, а
за додатним напрямом осі х, а ![]() — похідна функції
— похідна функції ![]() за додатним напрямом осі у.
за додатним напрямом осі у.
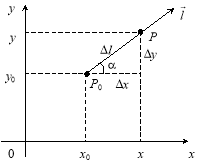
Рис. 1.23
Похідна за напрямом ![]() характеризує швидкість зміни функції
характеризує швидкість зміни функції ![]() у точці
у точці ![]() за напрямом l.
за напрямом l.
Теорема 1.18. Якщо функція ![]() має в точці
має в точці ![]() неперервні частинні похідні, то в цій точці існує похідна
неперервні частинні похідні, то в цій точці існує похідна ![]() за будь-яким напрямом
за будь-яким напрямом ![]() , причому
, причому
![]() (12)
(12)
де ![]() і
і ![]() — значення частинних похідних у точці
— значення частинних похідних у точці ![]() .
.
Доведення. За умовою теореми функція ![]() має в точці
має в точці ![]() неперервні частинні похідні, тому за теоремою 1.16 вона диференційовна в цій точці:
неперервні частинні похідні, тому за теоремою 1.16 вона диференційовна в цій точці:
![]()
де ![]() ,
, ![]() — нескінченно малі величини при
— нескінченно малі величини при ![]()
![]() Тоді
Тоді
![]() .
.
Із трикутника ![]() (рис. 1.23) маємо:
(рис. 1.23) маємо:
![]() ,
, ![]()
Звідси
![]()
Якщо ![]() , то
, то ![]() ,
, ![]() , а отже
, а отже ![]()
![]() Звідси
Звідси
![]()
![]() Знайти похідну функції
Знайти похідну функції ![]() у точці
у точці ![]() за напрямом
за напрямом ![]()
● Знайдемо та обчислимо частинні похідні в точці ![]() функції
функції ![]() :
:
![]()
![]()
Тоді за формулою (12) маємо:
![]() .
.
Означення. Вектор з координатами ![]() , який характеризує напрям максимального зростання функції
, який характеризує напрям максимального зростання функції ![]() в точці
в точці ![]() , називається градієнтом функції
, називається градієнтом функції ![]() у цій точці і позначається
у цій точці і позначається ![]() :
:
![]() (13)
(13)
де i, j — одиничні орти.
![]() Знайти градієнт функції
Знайти градієнт функції ![]() у точці
у точці ![]() .
.
● Запишемо та обчислимо частинні похідні в точці ![]() :
:
![]() ;
; ![]()
Тоді згідно з (13) ![]() , або
, або ![]() .
.
Аналогічно для диференційовної функції ![]() у точці
у точці ![]() похідна за напрямом довільного одиничного вектора
похідна за напрямом довільного одиничного вектора ![]() ,
, ![]() подається так:
подається так:
![]()
Означення. Градієнтом диференційовної функції ![]() у точці
у точці ![]() називають вектор
називають вектор ![]()
![]() де
де ![]() — одиничні орти, а значення частинних похідних
— одиничні орти, а значення частинних похідних ![]() обчислені в точці
обчислені в точці ![]() .
.
Властивості:
1. ![]() . 2.
. 2. ![]() .
.
3. Якщо ![]() , то похідна
, то похідна ![]() досягає найбільшого значення при
досягає найбільшого значення при ![]() .
.
Самостійне вивчення №12
Тема: Означення визначеного інтеграла. Інтегральні суми. Методи підстановки та інтегрування за частинами у визначеному інтегралі. Площі плоских фігур та об’єми геометричних тіл. Застосування визначених інтегралів до обчислення площ, об’ємів, шляху. Поняття про подвійний інтеграл. Зведення подвійного інтегралу до повторного.
Література: О-1 с. 81-92, 112-117; О-2 с.287-312; О-4 с. 104-126;
О-5 с. 318-365; О-6 с. 230-266; Д-5 с. 239-279;
Д-6 с. 210-227.
В результаті самостійного вивчення студент повинен
знати:
- означення визначеного інтеграла;
- формулу Ньютона-Лейбніца;
- означення подвійного інтеграла;
вміти:
- обчислювати визначені інтеграли;
- використовувати метод підстановки та інтегрування частинами у визначеному інтегралі;
- використовувати визначений інтеграл для обчислення площ, об’ємів та шляху;
- зводити подвійний інтеграл до повторного та обчислювати його.
Короткі теоретичні відомості та методичні вказівки
Визначений інтеграл
Існує кілька підходів до викладання визначених інтегралів. Розглянемо основні, що мають історичні корені і найбільш близькі до початків інтегрального числення.
Підсумовування нескінченно малих
Нехай задано неперерву функцію на відрізку [a; b] і F(x) —будь-яка її первісна. Розіб’ємо відрізок [a; b] на n частин і утворимо різницю
F(b) – F(a) (1)
значень первісної на його кінцях.
Різниця (1) дорівнює сумі таких самих різниць, складених для відрізків, на які розбито даний:
![]() (2)
(2)
![]()
Рис. 2.1
За теоремою Лагранжа про скінченний приріст маємо:
F(хі) – F(хі – 1) = (хі – хі – 1)F(i – 1),
де i [хі; хі–1] (рис. 2.1).
Позначивши хі – хі–1 = хі–1 і врахувавши, що
F(i–1) = f(i–1),
рівність (2) подамо так:
F(b) – F(a) = f(0)х0 + f(1)х1 + … + f(n–1)хn – 1. (3)
Залежність (3) справджується лише для значень 0, 1, … n, які задовольняють теорему Лагранжа. Але коли необмежено збільшувати кількість n частин відрізка [a; b] так, щоб довжина відрізка хі – 1 прямувала до нуля, то рівність (3) виконуватиметься і різниця F(b) – F(a) буде сумою нескінченної кількості спадних доданків:
![]() (4)
(4)
Рівність (3) справджується не лише за певного, а й за будь-якого вибору точок 0, 1, … n–1, тому (4) є формулою суми нескінченно малих, яку вивели Лейбніц і Ньютон.
Поняття визначеного інтеграла. Перший підхід
Означення. Сума
![]()
називається інтегральною сумою, або сумою Рімана.
Означення. Скінченна границя І суми при ![]() називається визначеним інтегралом від функції f(x) на відрізку
називається визначеним інтегралом від функції f(x) на відрізку
[a; b] і позначається
![]() (5)
(5)
де а, b — відповідно нижня та верхня межі інтегрування, — знак інтеграла, введений Лейбніцем. (Лейбніц увів знак інтеграла як витягнуту букву S, що позначає підсумовування.) У разі існування границі І функція f(x) називається інтегровною на проміжку [a; b].
Вводячи поняття про визначений інтеграл як границю інтегральної суми й застосовуючи його позначення та формулу (5), рівність (4) можна переписати у вигляді:
![]() (6)
(6)
Це відома формула Ньютона—Лейбніца, яка поєднує диференціальне числення з інтегральним.
В інтегралі ![]() символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
![]()
Зауважимо, що означення визначеного інтеграла можна застосувати лише до обмеженої функції.
Теорема 2.7. (Необхідна умова інтегрування.) Інтегровна на проміжку [a; b] функція обмежена.
Доведення. Припустимо супротивне. Нехай функція f(x) на проміжку необмежена. Тоді за будь-якого розбиття проміжку на частини функція f(x) зберігає цю властивість хоча б в одній із частин. Завдяки вибору на цій частині точки можна зробити значення f(), а з нею і суму як завгодно великою. За цих умов скінченні границі для існувати не можуть.
Властивості визначеного інтеграла
Властивість 1. Визначений інтеграл є міра площі.
● Справді, інтегральна сума
![]() (7)
(7)
утворена з добутків виду
![]() (8)
(8)
Нехай і–1 = хі–1. Тоді добуток (8) є площа прямокутника, основу якого становить різниця хі – хі–1 = хі–1, а висоту — ордината f(xi–1). Отже, інтегральна сума (7) являє собою суму площ таких прямокутників, або площу східчастої фігури, вписаної у криволінійну трапецію АabB, обмежену кривою у = f(x) (рис. 2.2).

Рис. 2.2
Площа криволінійної трапеції АabB більша за інтегральну суму (7). Але якщо вибрати за точки і(і = 0, …, n – 1) праві кінці відрізків [хі–1; хі], то дістанемо фігуру, описану навколо криволінійної трапеції АabB. Тому площа криволінійної трапеції АabB дещо менша за інтегральну суму (7).
Границя інтегральної суми (7) при будь-якому виборі точок і і при ![]() за означенням є визначений інтеграл
за означенням є визначений інтеграл ![]() .
.
Отже, доходимо висновку:
Визначений інтеграл ![]() дорівнює площі криволінійної трапеції.
дорівнює площі криволінійної трапеції.
Властивість 2. При переставленні меж інтегрування визначений інтеграл змінює знак, не змінюючи абсолютної величини.
● Узявши a < b і а < x1 < x2 < … < xn–1 < b, за означенням дістанемо:
![]() .
.
Переставивши межі інтегрування а та b, розглядатимемо вже відрізок [b; a] і, узявши ті самі точки розбиття, дістанемо відрізки [хі; хі–1], а не [хі–1; хі]. Отже,
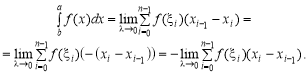
Звідси випливає таке співвідношення:
![]() (9)
(9)
![]() Зауваження. Цю властивість можна довести також за формулою Ньютона—Лейбніца (6), яка справджується для будь-яких а і b. Зокрема, вона виконується, коли числа а та b поміняти місцями:
Зауваження. Цю властивість можна довести також за формулою Ньютона—Лейбніца (6), яка справджується для будь-яких а і b. Зокрема, вона виконується, коли числа а та b поміняти місцями:
![]()
Таким чином, знову маємо формулу (9).
Наслідок. ![]()
● Справді, узявши у формулі (9) b = а, дістанемо
![]()
Властивість 3. (Поділ відрізка інтегрування.) Нехай точка c [а; b]. Тоді
![]() (10)
(10)
● Справді, якщо F(x) — будь-яка первісна для функції f(x) на відрізку [а; b], то F(x) є первісною і для функції f(x) на відрізках [а, с] і [с, b]. Отже, за формулою Ньютона—Лейбніца записуємо
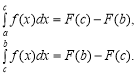
Звідси
![]()
Остання рівність і доводить формулу (10).
Геометрична інтерпретація
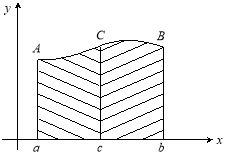
Рис. 2.3
Площа криволінійної трапеції АаbB дорівнює сумі площ криволінійних трапецій АасС і СсbB (рис. 2.3).
Властивість 4. (Знак визначеного інтеграла.)
1. Якщо f(x) > 0 для х (а; b), a < b, то ![]()
2. Якщо f(x) < 0 для х (а, b), a < b, то ![]()
● За означенням визначений інтеграл є границя інтегральної суми:
![]()
1. У разі f(x) > 0, a < b доданки f(і)хі інтегральної суми до-
датні, оскільки додатні обидва множники f(хі–1) і хі–1.
2. Якщо a > b, то хоча f(хі–1) > 0, множник хі–1 від’ємний. Справді:
хі–1 = хі – хі–1 і а > x1 > x2 > … > хі–1 > хі > … > b.
3. Розглядаючи доданки f(хі–1)хі–1 інтегральної суми, встановлюємо, що множник f(і) < 0, множник хі–1 додатний, оскільки
a < b.
Геометрична інтерпретація
1. Площа, обмежена кривою В'АВ, має різні знаки по різні боки кожної межі інтегрування а (рис. 2.4).
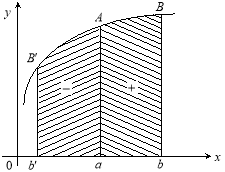
Рис. 2.4
2. Площі кривих, розміщених над віссю абсцис, вважаються додатними, а площі кривих, розміщених під віссю абсцис, — від’ємними (рис. 2.5).

Рис. 2.5
![]()
Знайти суму площ двох сусідніх хвиль синусоїди ![]()
● ![]() (рис. 2.6).
(рис. 2.6).
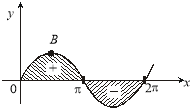
Рис. 2.6
Властивість 5. Якщо (х) > (х) для х (a; b), a < b, то справджується рівність:
![]()
● Визначимо знак різниці:
![]()
За властивістю 4 останній інтеграл додатний.
Властивість 6. Визначений інтеграл суми функцій подається як алгебраїчна сума інтегралів:
![]() (11)
(11)
● Розглянемо інтегральну суму
![]()
яку згідно з властивістю дистрибутивності можна розкласти на дві суми:
![]()
Переходячи до границі при ![]() , маємо:
, маємо:
![]()
тобто виконується (11).
Властивість 7. Сталий множник можна виносити за знак визначеного інтеграла:
![]() (12)
(12)
● За означенням визначеного інтеграла записуємо:
![]()
А оскільки в інтегральній сумі сталий множник можна винести за знак цієї суми, дістаємо:
![]()
Переходячи до границі, маємо:
![]()
Отже, виконується (6).
Властивість 8. Якщо функція f(x) інтегровна на [a; b] і а < b, то
![]() (13)
(13)
● Рівність (13) легко дістати, перейшовши безпосередньо до границь у нерівності для інтегральних сум:
![]()
Властивість 9. Якщо f(x) інтегровна на [a; b], де а < b, і якщо на цьому проміжку виконується нерівність
![]()
то
![]() (14)
(14)
● Рівність (14) дістанемо, безпосередньо перейшовши до границь у нерівності
![]()
та взявши до уваги, що ![]() .
.
Властивість 10. (Теорема про середнє значення.) Нехай f(x) — інтегровна на [a; b] функція і на всьому проміжку ![]() Тоді
Тоді
![]() (15)
(15)
де ![]()
Доведення. Якщо а < b, то за властивістю 9 маємо:
![]() .
.
Звідси
![]() .
.
Узявши
![]() ,
,
знайдемо рівність (14).
Якщо а > b, то на підставі аналогічних міркувань (з преставленням межі інтегрування) дістаємо (14).
Випадок неперервної функції f(x). Якщо числа m i M — відповідно найбільше і найменше значення функції (вони існують за теоремою Вейєрштрасса), то за теоремою Больцано—Коші проміжного значення функція f(x) набуває в деякій точці с проміжку [a, b].
Таким чином,
![]()
Геометрична ілюстрація. Нехай f(x) 0. Розглянемо криволінійну фігуру АВСD, обмежену кривою у = f(x) (рис. 2.7). Площа такої фігури (виражена визначеним інтегралом) дорівнює площі прямокутника з основою АВ і висотою LM.
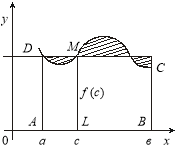
Рис. 2.7
Властивість 11. (Узагальнена теорема про середнє значення.)
Нехай виконуються такі умови:
1) f(x) і g(x) — інтегровні у проміжку [a; b];
2) m f(x) M;
3) g(x) 0 (або g(x) 0).
Тоді
![]() де m M. (16)
де m M. (16)
Доведення. Не порушуючи загальності, візьмемо g(x) 0 і а < b. За такої умови дістанемо:
![]() .
.
Звідси згідно з властивостями 6 і 3 маємо:
![]() . (17)
. (17)
А оскільки g(x) 0, то згідно з властивістю 5
![]() .
.
Якщо цей інтеграл дорівнює нулеві, то з попередніх нерівностей випливає співвідношення:
![]() ,
,
а отже, і твердження теореми.
Якщо інтеграл більший від нуля, то ділячи на нього всі частини нерівності (17) і вважаючи, що
 ,
,
дістаємо твердження, яке потрібно довести.
Випадок неперервної функції f(x). Формулу (16) можна записати у вигляді
![]()
Зведення подвійного інтеграла до повторного
І. Випадок прямокутної області. Нехай область інтегрування є прямокутник
![]()
зі сторонами, паралельними координатним осям (див. рис. 2.31) і ![]() — неперервна в цій області функція. Якщо зафіксувати
— неперервна в цій області функція. Якщо зафіксувати ![]() , то
, то ![]() буде неперервною функцією змінної х. Тому існує інтеграл
буде неперервною функцією змінної х. Тому існує інтеграл ![]() який є неперервною функцією змінної
який є неперервною функцією змінної ![]() . Таким чином, функцію
. Таким чином, функцію ![]() можна інтегрувати на відрізку
можна інтегрувати на відрізку ![]() . Отже, дістаємо повторний інтеграл
. Отже, дістаємо повторний інтеграл
![]() (16)
(16)
Цей процес можна здійснити в оберненому порядку: спочатку обчислити функцію від х, визначену рівністю ![]() , а потім функцію
, а потім функцію ![]() зінтегрувати за х від a до b. У результаті дістанемо повторний інтеграл:
зінтегрувати за х від a до b. У результаті дістанемо повторний інтеграл:
![]() (17)
(17)
Теорема 2.23. Нехай функція ![]() неперервна в замкненому прямокутнику D. Тоді виконується рівність
неперервна в замкненому прямокутнику D. Тоді виконується рівність
![]()
![]() (18)
(18)
Обчислити інтеграл
![]()
![]() .
.
Маємо:

2. Випадок криволінійної області. Нехай область D обмежена двома неперервними кривими ![]() і
і ![]() ,
, ![]() , і вертикальними відрізками
, і вертикальними відрізками ![]() і
і ![]() (рис. 2.32). Нехай будь-яка пряма, паралельна осі у, перетинає межу області D не більш ніж у двох точках. Тоді справджується формула:
(рис. 2.32). Нехай будь-яка пряма, паралельна осі у, перетинає межу області D не більш ніж у двох точках. Тоді справджується формула:
![]() (19)
(19)
У (19) спочатку функцію ![]() інтегруємо за змінною у від
інтегруємо за змінною у від ![]() до
до ![]() , вважаючи х сталою, а потім результат інтегруємо за х на відрізку [a, b].
, вважаючи х сталою, а потім результат інтегруємо за х на відрізку [a, b].

Рис. 2.32
Якщо область D (рис. 2.33) визначається нерівностями ![]() ,
, ![]() , де
, де ![]() і
і ![]() — неперервні на відрізку [c; d], і будь-яка пряма, паралельна осі х, перетинає межу області не більш ніж у двох точках, то
— неперервні на відрізку [c; d], і будь-яка пряма, паралельна осі х, перетинає межу області не більш ніж у двох точках, то
![]() (20)
(20)

Рис. 2.33
 Обчислити інтеграл
Обчислити інтеграл
![]()
якщо D обмежена прямими у = х, у = 2х, х = 2, х = 3. (Рис. 2.34.)
● За формулою (19) маємо:
Рис. 2.34
 Обчислити інтеграл
Обчислити інтеграл
![]()
якщо D обмежена прямими у = 1, у = х, у = – х (рис. 2.35).
● За формулою (20) дістаємо:
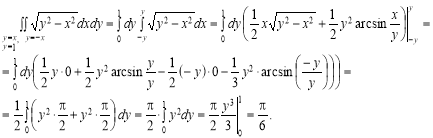
Рис. 2.35
![]() Зауваження. Довільну область з кусково-гладкою межею можна розбити на скінченну кількість областей, кожна з яких має вигляд, показаний на рис. 2.33. Тому обчислення подвійного інтеграла завжди зводиться до обчислення повторних інтегралів.
Зауваження. Довільну область з кусково-гладкою межею можна розбити на скінченну кількість областей, кожна з яких має вигляд, показаний на рис. 2.33. Тому обчислення подвійного інтеграла завжди зводиться до обчислення повторних інтегралів.
 Обчислити інтеграл
Обчислити інтеграл
![]()
якщо D — область, обмежена прямими х = у, у = 2х, у = 6 – х (рис. 2.36).
Рис. 2.36
Відрізком АВ поділимо D на два трикутники D1 і D2. Тоді
![]() .
.
За формулою (19) маємо:
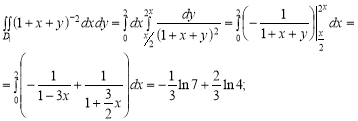
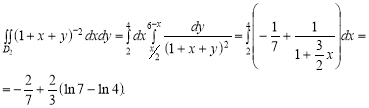
Отже,
![]()
![]()
 Змінити порядок інтегрування в повторному інтегралі
Змінити порядок інтегрування в повторному інтегралі
![]()
● Область ![]() зображено на рис. 2.37.
зображено на рис. 2.37.
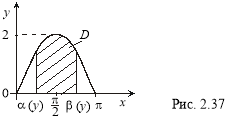
Проекцією множини D на вісь у є відрізок [0; 2]. Кожна пряма ![]() перетинає множину D по відрізках з кінцями (у) і (у), які знаходимо як розв’язок рівняння
перетинає множину D по відрізках з кінцями (у) і (у), які знаходимо як розв’язок рівняння ![]() на відрізку [0; ];
на відрізку [0; ]; ![]() ,
, ![]() . Таким чином, множина D задається нерівностями:
. Таким чином, множина D задається нерівностями:
![]() .
.
За формулою (19) маємо:
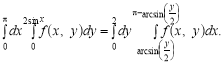
![]() Зауваження. Зміна порядку інтегрування в повторному інтегралі іноді істотно спрощує його обчислення.
Зауваження. Зміна порядку інтегрування в повторному інтегралі іноді істотно спрощує його обчислення.
Самостійне вивчення №13
Тема: Основні поняття та означення. Диференціальні рівняння першого порядку. Задача Коші. Теорема про існування і єдність розв’язків. Задачі, що зводяться до диференціальних рівнянь. Диференціальні рівняння з відокремленими змінними. Лінійні та однорідні рівняння першого порядку. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами. Загальний та частинний розв’язок.
Література: О-1 с. 92-103; О-2 с. 315-332; О-4 с. 134-144;
О-5 с. 369-393; О-6 с. 267-290; Д-5 с. 239-279;
Д-6 с. 210-227.
В результаті самостійного вивчення студент повинен
знати:
- означення диференціального рівняння, диференціального рівняння з відокремленими змінними, лінійного диференціального рівняння;
вміти:
- розв’язувати диференціальні рівняння з відокремленими змінними, лінійні диференціального рівняння;
- розв’язувати задачу Коші.
Короткі теоретичні відомості та методичні вказівки
Теорема 1.17. Нехай на множині D визначено складену функцію ![]() , де
, де ![]() ,
, ![]() , і нехай функції
, і нехай функції ![]() ,
, ![]() мають у деякому околі точки
мають у деякому околі точки ![]() неперервні частинні похідні, а функція
неперервні частинні похідні, а функція ![]() має неперервні частинні похідні в деякому околі точки
має неперервні частинні похідні в деякому околі точки ![]() , де
, де ![]() ,
, ![]() . Тоді складена функція
. Тоді складена функція ![]() диференційовна в точці
диференційовна в точці ![]() , причому
, причому
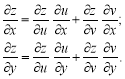
![]()
Доведення. За умовою теореми функції ![]() і
і ![]() мають неперервні частинні похідні в деякому околі точки
мають неперервні частинні похідні в деякому околі точки ![]() . Тому за теоремою 1.16 вони диференційовні в точці
. Тому за теоремою 1.16 вони диференційовні в точці ![]() :
:
![]()
![]()
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() при
при ![]() ,
, ![]() .
.
Надавши приростів лише аргументу х, дістанемо
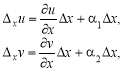 (10)
(10)
де ![]() ,
, ![]() при
при ![]() ,
, ![]()
Знайдемо приріст функції ![]() за х. За умовою теореми функція
за х. За умовою теореми функція ![]() має неперервні частинні похідні в деякому околі точки
має неперервні частинні похідні в деякому околі точки ![]() , а тому вона диференційовна в цій точці:
, а тому вона диференційовна в цій точці:
![]() (11)
(11)
Підставляючи у (11) рівності (10), дістаємо:
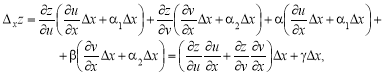
де
![]() —
—
нескінченно мала величина при ![]() .
.
Тоді
![]() .
.
Аналогічно можна довести й формулу (9).
Диференційовність функції ![]() випливає з неперервності частинних похідних
випливає з неперервності частинних похідних ![]() і
і ![]() .
.
![]() Знайти
Знайти ![]() і
і ![]() для функції
для функції ![]() , якщо
, якщо ![]()
![]()
● За формулами (8) і (9) маємо:
![]() ;
;
![]() .
.
![]() Знайти повний диференціал функції , якщо
Знайти повний диференціал функції , якщо ![]() ,
, ![]() ,
, ![]()
● З урахуванням формул (2) і формул (8), (9) дістаємо:
● ![]()
![]()
![]() .
.
Самостійне вивчення №14
Тема: Основні поняття та означення. Числові ряди. Збіжність рядів. Властивості збіжних рядів. Гармонійний ряд. Необхідна умова збіжності рядів. Достатні умови збіжності рядів з додатними членами: ознака порівняння, ознака д’Аламбера, ознака Коші. Знакозмінні ряди. Абсолютна та умовна збіжність. Степеневі ряди. Теорема Абеля. Область збіжності степеневого ряду. Розклад функції в ряд Тейлора та Маклорена.
Література: О-2 с. 335-358; О-4 с. 145-160; О-6 с. 291-310;
Д-5 с. 281-320; Д-6 с. 176-186.
В результаті самостійного вивчення студент повинен
знати:
- основні поняття та означення ряду;
вміти:
- досліджувати ряди на збіжність;
- розв’язувати задачі лінійного програмування.
Короткі теоретичні відомості та методичні вказівки
Ряди
Ряди є основним обчислювальним засобом. Навіть у калькуляторах при обчисленні значень функцій використовуються ряди. Ряди застосовуються для наближених обчислень.
5.1. Основні поняття і означення
Нехай задано послідовність чисел u1, u2, …, un … .
Означення. Вираз
![]()
називається рядом, а самі числа u1, u2, …, un… називаються членами ряду. Вираз un як функція від n називається загальним членом ряду.
Означення. Скінченні суми
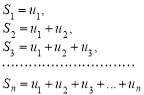 (1)
(1)
називаються частинними сумами ряду.
Означення. Ряд ![]() називається збіжним, якщо існує границя частинних сум ряду
називається збіжним, якщо існує границя частинних сум ряду
![]() . (2)
. (2)
Границя частинних сум (2) називається сумою ряду. Якщо границя (2) не існує, то ряд ![]() називається розбіжним.
називається розбіжним.
![]() Дослідимо збіжність числового ряду
Дослідимо збіжність числового ряду
![]()
● Знайдемо значення частинної суми ряду:
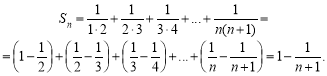
Шукаємо границю частинних сум ряду:
![]()
Границя існує, отже, розглядуваний ряд збігається і його сума дорівнює 1.
![]() Розглянемо ряд геометричної прогресії
Розглянемо ряд геометричної прогресії
![]() (3)
(3)
І. Якщо q 1, можемо знайти частинну суму ряду
![]()
ІІ. Якщо |q| < 1, qn 0 при n + і при цьому існує границя частинних сум ряду
![]()
ряд (3) збігається.
Якщо |q| > 1, границя частинних сум не існує і ряд (3) розбігається.
Якщо q = 1, маємо ряд
![]()
Його частинні суми
![]()
Границя частинних сум не існує, отже, при q = 1 ряд (3) розбігається.
Якщо q = – 1, маємо ряд
![]()
і частинні суми
![]()
Границя частинних сум Sn ряду не існує, і ряд (3) розбігається.
Наведемо необхідні і достатні умови збіжності числового ряду.
Теорема 5.1. (Критерій Коші.) Для того, щоб ряд ![]() збігався, необхідно і достатньо, щоб для будь-якого > 0 знайшлось таке N = N(), що при будь-якому р > 0, n N виконується нерівність
збігався, необхідно і достатньо, щоб для будь-якого > 0 знайшлось таке N = N(), що при будь-якому р > 0, n N виконується нерівність
![]() (4)
(4)
Іншими словами, збіжність ряду ![]() рівносильна тому, що сума будь-якої кількості членів ряду, наступних за членом ряду з достатньо великим номером, може бути скільки завгодно малою.
рівносильна тому, що сума будь-якої кількості членів ряду, наступних за членом ряду з достатньо великим номером, може бути скільки завгодно малою.
Означення. Ряд
![]() (5)
(5)
називається залишком ряду ![]()
Очевидна теорема.
Теорема 5.2. Для того, щоб збігався ряд ![]() необхідно і достатньо, щоб збігався залишок ряду.
необхідно і достатньо, щоб збігався залишок ряду.
Доведення. Розглянемо при фіксованому значенні n частинну суму ряду (5).
![]()
Існування границі ![]() рівносильне існуванню границі
рівносильне існуванню границі ![]() , що доводить правильність теореми.
, що доводить правильність теореми.
З теореми 5.2 випливає, що збіжність ряду ![]() не зміниться, якщо відкинути скінченну кількість перших членів.
не зміниться, якщо відкинути скінченну кількість перших членів.
З критерію Коші випливає, що збіжність ряду ![]() рівносильна тому, щоб усі частинні суми залишку ряду (5) були скільки завгодно малі, якщо номер n достатньо великий.
рівносильна тому, щоб усі частинні суми залишку ряду (5) були скільки завгодно малі, якщо номер n достатньо великий.
Теорема 5.3. (Необхідна умова збіжності.) Для того щоб ряд ![]() збігався, необхідно, щоб загальний член ряду прямував до нуля, тобто щоб виконувалась умова
збігався, необхідно, щоб загальний член ряду прямував до нуля, тобто щоб виконувалась умова
![]() . (6)
. (6)
Доведення. Нехай ряд збігається, тобто існує границя частинних сум ряду
![]()
З рівності un = Sn – Sn–1 випливає, що існує границя
![]()
що і доводить правильність теореми.
Умова (6) не є достатньою для збіжності ряду, що можна бачити на прикладі так званого гармонійного ряду
![]() (7)
(7)
![]() Дослідити збіжність ряду (7).
Дослідити збіжність ряду (7).
● Оцінимо знизу деякі частинні суми:
![]() .
.
![]() , …
, …
Аналогічним способом отримаємо оцінку
![]()
Оскільки частинні суми не обмежені згори, то не існує границя ![]() і гармонійний ряд розбігається. Хоча для гармонійного ряду (7) виконана необхідна умова збіжності (6)
і гармонійний ряд розбігається. Хоча для гармонійного ряду (7) виконана необхідна умова збіжності (6)
![]()
![]() Дослідимо збіжність ряду
Дослідимо збіжність ряду ![]()
● Шукаємо границю загального члена ряду
![]()
Оскільки загальний член ряду не прямує до нуля, то розглядуваний ряд розбігається.
![]() Розглянемо знову ряд геометричної прогресії (3)
Розглянемо знову ряд геометричної прогресії (3)
![]()
При |q| > 1 ряд розбігається, бо загальний член ряду un = аqn не прямує до нуля.
Властивості дій з рядами
Теорема 5.4. Задано числовий ряд
![]() (8)
(8)
Якщо помножити члени ряду на один і той самий числовий множник а 0 і дістати ряд
![]() (9)
(9)
то із збіжності ряду (8) випливає збіжність ряду (9), і навпаки, зі збіжності ряду (9) випливає збіжність ряду (3). При цьому для сум ряду справджується рівність:
![]()
Отже, дії множення на число і підсумовування переставні.
Теорема 5.5. Якщо два ряди збігаються, то їх можна почленно додавати і віднімати, тобто
![]() (10)
(10)
Теорема 5.6. Збіжність числового ряду не зміниться, якщо для нього приписати або відкинути скінченну кількість членів.
![]() Розглянемо збіжний ряд з нульовими членами
Розглянемо збіжний ряд з нульовими членами
![]()
Розкривши дужки, дістанемо збіжний ряд
1 – 1 + 2 – 2 + 3 – 3 + … + n – n + …,
загальний член якого не прямує до нуля.
Ознаки збіжності рядів
з додатними членами
Найбільш часто використовуються ознаки збіжності рядів з додатними членами.
5.2.1. Необхідна і достатня умова збіжності ряду
з додатними членами
Розглядається ряд з додатними членами
![]() (11)
(11)
Частинні суми ряду монотонно зростають, бо
![]()
Звідси випливає правильність такої теореми.
Теорема 5.7. Для того, щоб ряд з додатними членами збігався, необхідно і достатньо, щоб усі його частинні суми були обмежені зверху.
Доведення. Якщо ряд (11) збігається, то існує границя послідовності частинних сум. Відомо, що збіжна послідовність обмежена.
Нехай послідовність частинних сум ряду обмежена зверху. За теоремою Вейєрштрасса монотонно зростаюча обмежена послідовність має границю. Отже, послідовність частинних сум ряду має границю і ряд збігається.
Ознаки порівняння
Розглядаємо два ряди з додатними членами
![]() (12)
(12)
![]() (13)
(13)
Теорема 5.8. Нехай з деякого номера n виконується нерівність un vn. Тоді із збіжності ряду (13) випливає збіжність ряду (12), а із розбіжності ряду (12) випливає розбіжність ряду (13).
Доведення. Оскільки відкидання скінченної кількості членів ряду не впливає на його збіжність, то можна вважати, що нерівність un vn виконується для всіх членів рядів. Якщо збігається ряд (13), то всі його частинні суми обмежені зверху. З огляду на це всі частинні суми ряду (12) теж обмежені зверху і, отже, ряд (12) збігається.
Якщо ряд (12) розбігається, то ряд (13) не може збігатися, бо за доведеним вище із збіжності ряду (13) випливає збіжність ряду (12). Теорему доведено.
При виконанні нерівності un vn кажуть, що ряд (13) мажорує ряд (12).
![]() Дослідимо збіжність числового ряду
Дослідимо збіжність числового ряду
![]() (14)
(14)
● Візьмемо збіжний ряд порівняння
![]() (15)
(15)
Оскільки виконуються нерівності
![]()
то за теоремою 2 ряд (4) збігається.
На практиці найбільш зручна ознака порівняння у граничній формі.
Теорема 5.9. Нехай для членів рядів (12), (13) існує границя
![]()
Тоді обидва ряди (12), (13) збігаються або розбігаються одночасно. Якщо l = 0, то зі збіжності ряду (12) випливає збіжність ряду (13). Якщо l = + , то з розбіжності ряду (13) випливає розбіжність ряду (12).
Доведення. Нехай 0 < l < . Для довільного > 0, < l знайдеться номер N = N(), такий що при n > N виконуватимуться не-
рівності:
![]()
З нерівностей (l – )vn < un < (l + )vn і збіжності ряду (12) випливає збіжність ряду ![]() З розбіжності ряду (12)
З розбіжності ряду (12) ![]() що остаточно доводить правильність теореми.
що остаточно доводить правильність теореми.
![]() Порівняємо збіжність рядів (14), (15), що мають загальні члени
Порівняємо збіжність рядів (14), (15), що мають загальні члени ![]()
![]()
● Шукаємо границю відношення загальних членів
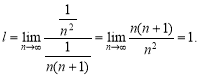
Згідно з теоремою 5.9 обидва ряди (14), (15) збігаються або розбігаються одночасно. Оскільки ряд (15) збігається, то й ряд (14) збігається.
![]() Дослідимо збіжність ряду
Дослідимо збіжність ряду ![]() порівнюючи з розбіжним гармонійним рядом
порівнюючи з розбіжним гармонійним рядом ![]() Оскільки існує границя
Оскільки існує границя
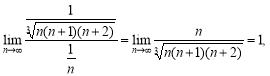
то досліджуваний ряд також розбігається.
Ознака Даламбера
Теорема 5.10. Якщо для ряду з додатними членами
![]() (16)
(16)
починаючи з деякого номера n N виконується нерівність
![]() (17)
(17)
то ряд (16) збігається. Якщо починаючи з деякого номера n N виконується нерівність
![]() (18)
(18)
то ряд розбігається.
Доведення. З нерівності (17) випливає, що справджуються нерівності
![]()
Отже, члени ряду
![]() (19)
(19)
мажоруються членами збіжного ряду
![]()
Звідси випливає збіжність ряду (19) і, отже, збіжність ряду (16).
Якщо виконується нерівність (18), то справджується нерівність
![]()
Оскільки загальний член ряду не прямує до нуля, то ряд (16) розбігається. Теорему доведено.
![]() Дослідимо збіжність ряду
Дослідимо збіжність ряду
![]() .
.
● Дамо оцінку відношення членів ряду при n 1

З теореми 5.10 випливає збіжність ряду, який розглядається.
Теорема 5.11. (Ознака Даламбера у граничній формі.)
Якщо для ряду (16) з додатними членами існує границя
![]()
то при q < 1 ряд збігається, при q > 1 ряд розбігається, при q = 1 ряд може збігатися і розбігатися.
Доведення. Якщо q < 1, то при достатньо великих значеннях n буде виконуватись нерівність ![]() і, отже, з огляду на теорему 5.10 ряд (16) збігається.
і, отже, з огляду на теорему 5.10 ряд (16) збігається.
При q > 1 достатньо великих значеннях і буде виконуватися нерівність ![]() і, отже, ряд (16) буде розбіжним.
і, отже, ряд (16) буде розбіжним.
При q = 1 ряд (6) може збігатися або розбігатися.
![]() Розглянемо чисельний ряд
Розглянемо чисельний ряд
![]()
Знайдемо границю відношення членів ряду
![]()
З теореми 5.11 випливає збіжність ряду.
![]() Дослідимо збіжність ряду
Дослідимо збіжність ряду
![]()
де а — параметр (а > 0).
● Знаходимо границю
![]()
Отже, при а < 2 ряд розбігається, а при а < 2 ряд збігається.
![]() Дослідимо за ознакою Даламбера розбіжний гармонійний ряд
Дослідимо за ознакою Даламбера розбіжний гармонійний ряд ![]() і збіжний ряд
і збіжний ряд ![]()
● Для першого ряду знаходимо
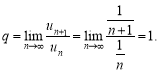
Для другого ряду маємо
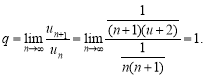
Отже, при q = 1 ряди можуть розбігатися або збігатися.
Радикальна ознака збіжності Коші
Теорема 5.12. Якщо для ряду з додатними членами
![]() (20)
(20)
починаючи з деякого номера n N виконується нерівність
![]()
то ряд збігається. Якщо починаючи з деякого номера n N виконується нерівність ![]() , то ряд розбігається.
, то ряд розбігається.
Доведення. Якщо при n N виконується нерівність ![]() то
то ![]() і ряд (20) збігається, бо мажорується членами збіжної геометричної прогресії. Якщо
і ряд (20) збігається, бо мажорується членами збіжної геометричної прогресії. Якщо ![]() то
то ![]() і розбігається, бо загальний член ряду не прямує до нуля.
і розбігається, бо загальний член ряду не прямує до нуля.
![]() Дослідимо збіжність ряду
Дослідимо збіжність ряду
![]()
● Оскільки виконується нерівність
![]()
то ряд, що досліджується, збігається.
Теорема 5.13. (Радикальна ознака Коші у граничній формі.)
Якщо для ряду (20) з додатними членами існує границя
![]()
то при q < 1 ряд збігається, при q > 1 ряд розбігається, а при q = 1 ряди можуть збігатися або розбігатися.
Доведення. Дослідимо збіжність ряду
![]()
● Знаходимо границю
![]()
При ![]() ряд збігається.
ряд збігається.
![]() Дослідимо збіжність ряду з параметром а
Дослідимо збіжність ряду з параметром а
![]()
● Знаходимо границю
![]()
При а > 0 ряд розбігається, при а < 0 ряд збігається.
![]() Дослідимо за допомогою радикальної ознаки збіжність розбіжного ряду
Дослідимо за допомогою радикальної ознаки збіжність розбіжного ряду ![]() і збіжного ряду
і збіжного ряду ![]()
● Знаходимо границі
![]() і
і
![]()
Отже, при q = 1 ряд може бути розбіжним або збіжним.
![]() Зауваження. Значення границі q в ознаці Даламбера збігається зі значенням границі q в радикальній ознаці Коші. При q = 1 доцільно застосувати наведену далі інтегральну ознаку Коші.
Зауваження. Значення границі q в ознаці Даламбера збігається зі значенням границі q в радикальній ознаці Коші. При q = 1 доцільно застосувати наведену далі інтегральну ознаку Коші.
Інтегральна ознака збіжності Коші
Інтегральна ознака збіжності заснована на порівнянні ряду з невласним інтегралом.
Нехай для ряду з додатними членами
![]()
вдалося знайти неперервну, монотонно спадну при х 1 функцію у = f(x) таку, що un = f(n) (n = 1, 2, 3, …) (див. рис. 5.1).
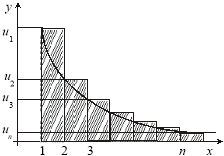
Рис. 5.1
Теорема 5.14. Якщо функція у = f(x) неперервна і монотонно спадає при х 1, то невласний інтеграл
![]() (21)
(21)
і ряд
![]() (22)
(22)
збігаються або розбігаються одночасно.
Доведення. З огляду на монотонне спадання функції виконується нерівність
![]()
Підсумовуючи ці нерівності, дістаємо
![]()
Якщо збігається невласний інтеграл, то з обмеженості частинних сум ряду ![]() випливає збіжність ряду (21). Якщо збігається ряд, то з обмеженості інтеграла
випливає збіжність ряду (21). Якщо збігається ряд, то з обмеженості інтеграла ![]() випливає збіжність невласного інтеграла (21). Теорему доведено.
випливає збіжність невласного інтеграла (21). Теорему доведено.
![]() Дослідимо збіжність гармонійного ряду
Дослідимо збіжність гармонійного ряду ![]()
● Оскільки ![]() то можемо скористатися функцію
то можемо скористатися функцію ![]()
Це неперервна, монотонно спадна при х 1 функція. Отже, збіжність гармонійного ряду рівносильна збіжності невласного інтеграла
![]()
Оскільки невласний інтеграл розбіжний, то ряд також розбіжний.
![]() Дослідимо збіжність
Дослідимо збіжність
![]() (23)
(23)
● Використаємо функцію ![]() яка при х 1 неперервна і монотонно спадає. Тому збіжність ряду рівносильна збіжності невласного інтеграла
яка при х 1 неперервна і монотонно спадає. Тому збіжність ряду рівносильна збіжності невласного інтеграла
Отже, ряд (23) збігається при s > 1 і розбігається при s 1.
Наведемо окремі випадки ряду (23). Ряд
![]()
розбігається, бо ![]() . Ряд
. Ряд
![]()
збігається, бо s = 2 > 1.
5.2.6. Економічний приклад
Якщо 100і — відсоток нарахування на вкладену суму, то ![]() називається множником дисконту. Через k років вкладена сума kbk набуває значення bk. Загальна сума вкладень за n років становить:
називається множником дисконту. Через k років вкладена сума kbk набуває значення bk. Загальна сума вкладень за n років становить:
![]()
Якщо прибуток від кожного вкладу буде сталим, тобто bk = b, то маємо
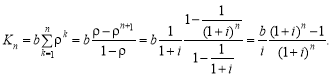
Звідси випливає, що
![]() .
.
Якщо прибуток bk змінюється за лінійним законом
![]() ,
,
то для загальної суми вкладень знаходимо вираз
![]()
Обчислимо значення сум
![]()
Звідси випливає, що
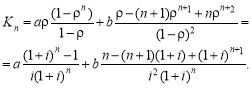
У границі при n + дістаємо пропорційний вираз
![]()
Якщо прибуток зростає за законом
![]()
то маємо вираз
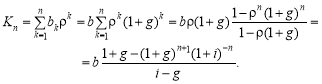
Аналогічно можна знайти значення Kn у разі інших законів отримання прибутку від кожного річного вкладу.
. Збіжність рядів
зі знакозмінними членами
5.3.1. Знакопочергові ряди.
Ознака збіжності Лейбніца
Означення. Ряд виду
![]() (24)
(24)
де аn > 0 (n = 1, 2, 3, …), називається знакопочерговим рядом.
Лейбніц указав достатню умову збіжності ряду (24).
Теорема 5.15. Нехай у знакопочерговому ряді (24) послідовність аn(n = 1, 2, 3, …) монотонно спадає. Якщо
![]()
ряд (24) збігається і його сума не перевищує а1.
Доведення. Розглянемо послідовність парних частинних сум ряду (24). Згідно з нерівностями
а1 а2 а3 а4 …
Послідовність частинних сум
![]()
монотонно зростає. Суми Sn можна подати у вигляді
![]()
звідси випливає, що S2n a1 (n = 1, 2, 3, …). Монотонно зростаюча, обмежена послідовність S2n збігається, тобто існує границя
![]()
Розглянемо послідовність непарних частинних сум.
![]()
Оскільки послідовності парних і непарних частинних сум прямують до однієї й тієї самої границі, то ряд (24) збігається.
Теорему доведено.
![]() Дослідимо збіжність знакопочергового ряду
Дослідимо збіжність знакопочергового ряду
![]()
Усі умови теореми 5.15 виконані, і тому ряд збігається. Абсолютна й умовна збіжність
Розглянемо довільний числовий ряд
![]() (25)
(25)
Означення. Ряд (25) називається абсолютно збіжним, якщо збігається ряд
![]() (26)
(26)
Збіжний ряд (25) називається умовно збіжним, якщо ряд (26) розбіжний.
![]() Ряд
Ряд ![]() є умовно збіжним, бо ряд
є умовно збіжним, бо ряд ![]() розбіжний.
розбіжний.
Очевидно, що із збіжності ряду (26) випливає збіжність ряду (25), бо члени ряду (25) можуть мати різні знаки.
Теорема 5.16. Абсолютно збіжний ряд збігається.
Доведення. Нехай збігається ряд (26). Для будь-якого > 0 знайдеться N = N() таке, що при n N, р > 0 буде виконана нерівність
![]()
При цьому буде також виконана нерівність
![]()
тобто ряд (25) також збігатиметься.
Оскільки для рядів з додатними членами відомі достатні ознаки збіжності, то їх можна використовувати для дослідження збіжності рядів за знакопочерговими членами.
Теорема 5.17. Якщо для знакопочергового ряду
![]()
існують границі
![]() ,
,
![]() то при q < 1 ряд абсолютно збіжний, а при q > 1 — розбіжний.
то при q < 1 ряд абсолютно збіжний, а при q > 1 — розбіжний.
Дослідимо збіжність ряду
![]()
● Знаходимо границю
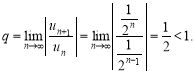
Отже, ряд, що розглядається, збігається абсолютно.
Раніше відмічалося, що в довільному ряді не можна переставляти члени ряду. Наведемо без доведення такі твердження.
Теорема 5.18. Якщо ряд збігається абсолютно, то за будь-якої перестановки членів ряд буде збігатися і сума його не змінюватиметься.
Теорема 5.19. (Теорема Рімана.) Якщо ряд збігається умовно і s — будь-яке наперед задане число, то завжди можна переставити члени ряду так, щоб сума отриманого ряду дорівнювала s.
Дамо пояснення до теореми Рімана. Умовна збіжність ряду виконується завдяки тому, що додатні і від’ємні члени взаємно знищуються. Якщо скласти ряд лише із додатних членів і ряд лише із від’ємних членів, то ці ряди розбігаються. Отже, можна почергово обирати лише додатні або від’ємні числа так, щоб значення частинних сум було як можна ближче до значення s. При цьому сума ряду дорівнюватиме s.
![]() Розглянемо ряд Лейбніца
Розглянемо ряд Лейбніца
![]()
Переставимо члени ряду так, щоб після додатного члена стояли два від’ємні.
При цьому дістанемо ряд
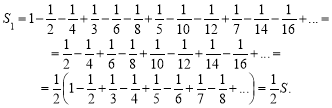
За такого переставлення членів ряду сума ряду зменшилась удвічіАбсолютна й умовна збіжність
Розглянемо довільний числовий ряд
![]() (25)
(25)
Означення. Ряд (25) називається абсолютно збіжним, якщо збігається ряд
![]() (26)
(26)
Збіжний ряд (25) називається умовно збіжним, якщо ряд (26) розбіжний.
![]() Ряд
Ряд ![]() є умовно збіжним, бо ряд
є умовно збіжним, бо ряд ![]() розбіжний.
розбіжний.
Очевидно, що із збіжності ряду (26) випливає збіжність ряду (25), бо члени ряду (25) можуть мати різні знаки.
Теорема 5.16. Абсолютно збіжний ряд збігається.
Доведення. Нехай збігається ряд (26). Для будь-якого > 0 знайдеться N = N() таке, що при n N, р > 0 буде виконана нерівність
![]()
При цьому буде також виконана нерівність
![]()
тобто ряд (25) також збігатиметься.
Оскільки для рядів з додатними членами відомі достатні ознаки збіжності, то їх можна використовувати для дослідження збіжності рядів за знакопочерговими членами.
Теорема 5.17. Якщо для знакопочергового ряду
![]()
існують границі
![]() ,
,
![]() то при q < 1 ряд абсолютно збіжний, а при q > 1 — розбіжний.
то при q < 1 ряд абсолютно збіжний, а при q > 1 — розбіжний.
Дослідимо збіжність ряду
![]()
● Знаходимо границю
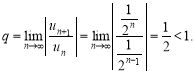
Отже, ряд, що розглядається, збігається абсолютно.
Раніше відмічалося, що в довільному ряді не можна переставляти члени ряду. Наведемо без доведення такі твердження.
Теорема 5.18. Якщо ряд збігається абсолютно, то за будь-якої перестановки членів ряд буде збігатися і сума його не змінюватиметься.
Теорема 5.19. (Теорема Рімана.) Якщо ряд збігається умовно і s — будь-яке наперед задане число, то завжди можна переставити члени ряду так, щоб сума отриманого ряду дорівнювала s.
Дамо пояснення до теореми Рімана. Умовна збіжність ряду виконується завдяки тому, що додатні і від’ємні члени взаємно знищуються. Якщо скласти ряд лише із додатних членів і ряд лише із від’ємних членів, то ці ряди розбігаються. Отже, можна почергово обирати лише додатні або від’ємні числа так, щоб значення частинних сум було як можна ближче до значення s. При цьому сума ряду дорівнюватиме s.
![]() Розглянемо ряд Лейбніца
Розглянемо ряд Лейбніца
![]()
Переставимо члени ряду так, щоб після додатного члена стояли два від’ємні.
При цьому дістанемо ряд

За такого переставлення членів ряду сума ряду зменшилась удвічі
. Степеневі ряди
Найбільш важливими для прикладних задач є степеневі ряди, які мають вигляд
![]() (6)
(6)
або більш загальний
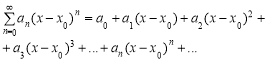 (7)
(7)
Оскільки заміна х – х0 на х зводить ряд виду (7) до ряду виду (6), то далі вивчаємо властивості степеневих рядів виду (6). Коефіцієнти аn називаються коефіцієнтами степеневого ряду.
5.5.1. Теорема Абеля
При дослідженні збіжності степеневих рядів використовується теорема Абеля.
Теорема 5.24. Якщо степеневий ряд (6) збігається при х = х1, х1 0, то він абсолютно збігається при |x| < |x1|. Якщо степеневий ряд розбігається при х = х2, то він розбігається при |x| > |x2|.
Доведення. Якщо степеневий ряд (6) збігається при х = х1, то загальний член ряду прямує до нуля, тобто
![]()
Оскільки збіжна послідовність обмежена, то знайдеться М > 0 таке, що при всіх значеннях n = 0, 1, 2, … виконується нерівність
![]()
Оцінимо члени ряду (6) за абсолютною величиною
![]()
Члени ряду (6) мажоруються членами геометричної прогресії зі знаменником ![]() . Отже, при q < 1, тобто при |x| < |x1| ряд (1) збігається абсолютно.
. Отже, при q < 1, тобто при |x| < |x1| ряд (1) збігається абсолютно.
Друге твердження теореми рівносильне першому.
Оскільки при будь-якому значенні х ряд (6) збігається або розбігається, то існує число R таке, що при |x| < R степеневий ряд (6) збігається, а при |x| > R — розбігається. Величина R називається радіусом збіжності степеневого ряду. У крайньому разі, коли R = 0, степеневий ряд розбігається при будь-якому х. При |x| = R ряд може збігатися або розбігатися.
Для пошуку радіуса збіжності можна використовувати формули, що випливають з ознак збіжності Даламбера і Коші
![]() (8)
(8)
Формули (8) придатні для випадку, коли границі існують.
![]()
Знайдемо область збіжності степеневого ряду
![]()
Для коефіцієнтів степеневого ряду і радіуса збіжності R маємо вирази
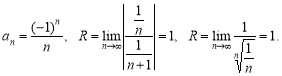
Отже, при |x| < 1 степеневий ряд збігається абсолютно. При х = 1 маємо числовий ряд
![]()
який збігається за ознакою Лейбніца. При х = – 1 ряд є гармонійним
![]()
який розбігається. Областю збіжності ряду є інтервал (– 1, 1].
![]() Знайдемо область збіжності степеневого ряду
Знайдемо область збіжності степеневого ряду
![]() (9)
(9)
● Формули (3) безпосередньо не придатні для пошуку радіуса збіжності, бо границі не існує. Тому безпосередньо використовуємо ознаку Даламбера для дослідження абсолютної збіжності ряду. Розглянемо ряд
![]()
Знаходимо границі
![]()
Ряд (9) збігається при |x|2 < 1 і розбігається при |x|2 > 1.
Отже, радіус збіжності R = 1. При х = 1 ряд (9) збігається за ознакою Лейбніца. Областю збіжності є відрізок [– 1, 1].
![]() Степеневий ряд
Степеневий ряд
![]()
збігається при будь-якому значенні х, бо
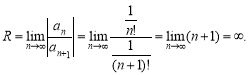
Степеневий ряд ![]()
розбігається при будь-якому значенні х 0, бо
![]()
Як видно із прикладу, в окремих випадках радіус збіжності може бути рівним 0 або .
5.5.2. Дії зі степеневими рядами
В основі дій зі степеневими рядами лежать такі теореми.
Теорема 5.25. Якщо R — радіус збіжності степеневого ряду
![]() , (10)
, (10)
то ряд збігається рівномірно при x [– , ] при 0 < < R.
Доведення. З теореми Абеля випливає збіжність ряду
![]() (11)
(11)
При х [– , ] виконані нерівності
![]()
з яких випливає рівномірна збіжність ряду (10), бо збіжний ряд (11) зі сталими членами мажорує функціональний ряд (10).
Теорема 5.26. При інтегруванні або диференціюванні степеневого ряду його радіус збіжності не змінюється.
З теорем 5.25, 5.26 випливає важливий результат.
Теорема 5.27. Якщо R > 0 — радіус збіжності степеневого ряду (10), то в області |x| < R степеневий ряд можна інтегрувати і диференціювати скільки завгодно разів.
![]() Знайдемо суму ряду при R = 1
Знайдемо суму ряду при R = 1
![]() .
.
● Інтегруючи рівність, знаходимо
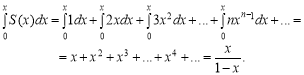
Диференціюючи здобуту рівність, маємо:
![]()
![]() Зауваження. При диференціюванні або інтегруванні степеневого ряду збіжність не змінюється, але може змінитися збіжність ряду на кінцях інтервалу збіжності при х = R.
Зауваження. При диференціюванні або інтегруванні степеневого ряду збіжність не змінюється, але може змінитися збіжність ряду на кінцях інтервалу збіжності при х = R.
![]() Розглянемо степеневий ряд
Розглянемо степеневий ряд
![]() (12)
(12)
Знаходимо радіус збіжності за ознакою Даламбера
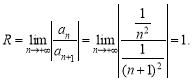
Ряд (12) збіжний при х = 1. При диференціюванні за х отримаємо степеневий ряд
![]() ,
,
який збігається при х = – 1 і розбігається при х = 1. У разі наступного диференціювання знаходимо ряд
![]() ,
,
який є розбіжним при х = 1.
Аналогічні результати справедливі для степеневого ряду
![]() (13)
(13)
Збіжність ряду можна вивчати у разі, коли коефіцієнти степеневого ряду аn, змінна х і стала а є комплексними числами. При цьому виявляється, що степеневий ряд (13) збігається у крузі
|x – а| < R і розбіжний при |x – а| > R. При цьому R — відстань від точки а до найближчої особливої точки суми ряду S(x).
Cуми збіжних степеневих рядів називаються аналітичними функціями. Властивості аналітичних функцій вивчає теорія функцій комплексного змінного.
5.5.3. Розклад функцій у степеневі ряди
Припустимо, що функцію f(x) можна розкласти в збіжний при |x| < R степеневий ряд
![]() (14)
(14)
Виразимо коефіцієнт ряду аn через функцію f (x).
Послідовно диференціюючи рівність (14), отримаємо
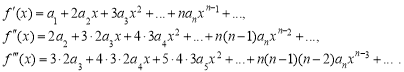
Підставляючи х = 0, дістаємо систему рівнянь
![]()
звідси знаходимо коефіцієнт аn
![]()
і розклад (14) набирає вигляду
![]() (15)
(15)
Цей ряд називається рядом Маклорена.
Якщо розкласти функцію f (x) у ряд за степенями (х – а), то отримаємо аналогічний результат і функція f (x) розкладається у степеневий ряд
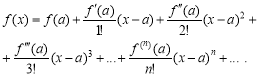 (16)
(16)
Степеневий ряд (10) називається рядом Тейлора.
Ряд (16) можна отримати з формули Тейлора із залишковим членом в інтегральній формі
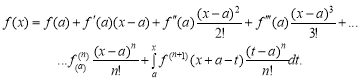 (17)
(17)
Використовуючи теорему про середнє, знаходимо залишковий член формули Тейлора у формі Лагранжа
![]() (18)
(18)
Теорема 5.28. Для того, щоб збігався ряд Тейлора (16) для скільки завгодно разів диференційовної функції f(x), необхідно і достатньо, щоб залишковий член формули Тейлора (18) прямував до нуля при n + .
![]() Дослідимо збіжність степеневого ряду
Дослідимо збіжність степеневого ряду
![]()
● За ознакою Даламбера знаходимо
![]()
Отже, степеневий ряд збігається при всіх значеннях х, і тому загальний член ряду прямує до нуля, тобто
![]() (19)
(19)
![]() Розкладемо в ряд Маклорена функцію f(x) = еx.
Розкладемо в ряд Маклорена функцію f(x) = еx.
● Знаходимо значення функції похідних у точці х = 0
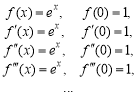
і за формулою (16) знаходимо розклад.
![]() (20)
(20)
Цей ряд збігається при всіх значеннях х. Доведемо, що степеневий ряд збігається до функції ех. Для цього розглянемо залишковий член
![]()
Оскільки залишковий член збігається до нуля при будь-якому х, то рівність (20) справедлива при будь-яких значеннях х. Зокрема при х = 1 знаходимо розклад для числа е
![]()
![]()
Розглянемо розклад функції f(x) = sin x у ряд Мак-
лорена.
● Знаходимо значення функції і похідних
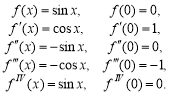
Із формули (21) знаходимо розклад функцій f(x) = sin x у ряд
![]() (21)
(21)
Залишковий член формули Тейлора
тому розклад (21) буде справедливий при будь-якому значенні х.
Диференціюючи рівність (21), знаходимо розклад функції f(x) = cos x у ряд Маклорена
![]() (22)
(22)
Зазначимо, що непарна функція у = sin x містить у своєму розкладі (21) лише непарні степені х, а парна функція у = cos x містить у своєму розкладі (22) лише парні степені х.
На основі формул (17)—(22) можна вивести відому формулу Ейлера
![]() (23)
(23)
Підставляючи в ряд (20) х = іу, дістанемо розклад
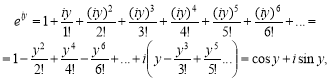
що доводить формулу Ейлера.
![]() Знайдемо біномінальний розклад Ньютона — розклад функції f(x) = (1 + х)m у ряд Маклорена.
Знайдемо біномінальний розклад Ньютона — розклад функції f(x) = (1 + х)m у ряд Маклорена.
● Знаходимо при х = 0 значення функції і її похідних
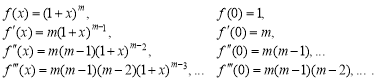
Звідси знаходимо ряд Маклорена
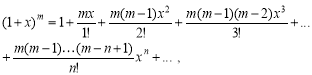 (24)
(24)
який збігається при |x| < 1.
Справедливість розкладу (24) буде доведена далі. В окремих випадках маємо розклад:
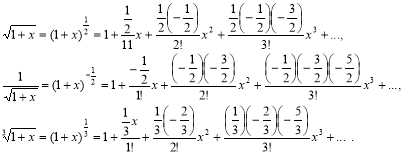
![]() Знайдемо розклад у ряд Маклорена функції f(x) = ln(1 + x).
Знайдемо розклад у ряд Маклорена функції f(x) = ln(1 + x).
● Із формули (24) знаходимо
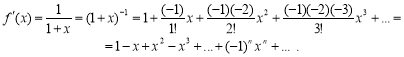
Інтегруючи рівність, знаходимо розклад у ряд
![]() (25)
(25)
справедливий при |x| < 1.
СПИСОК ЛІТЕРАТУРИ
Основна
- Казановський В.І. та ін. Вища математика. Конспект лекцій – НМЦ, 2003.
- Барковський В.В., Барковська Н.В. Математика для економістів. Ч. І. Вища математика. – К., 1999.
- Барковський В.В., Барковська Н.В. Математика для економістів. Ч. ІІ. Теорія ймовірностей та математична статистика – К., 1999.
- Литвин І.І. та ін. Вища математика. Навчальний посібник. – Львів, 2002.
- Лисичкин В.Т., Соловейчик И.Л. Математика. – М., 1991.
- Зайцев І.Л. Елементи вищої математики для технікумів. – К., 1973.
Додаткова
- Нелін Є.П. Алгебра і початки аналізу. 10 клас. Х., 2010.
- Бевз Г.П., Бевз В.Г. Математика. 11 клас. К, 2011.
- Шкіль М.І. та ін. Алгебра і початки аналізу. 10-11 кл. – К., 2001.
- Яковлев Г.Н. Алгебра и начала анализа. Ч. І. – М., 1977.
- Яковлев Г.Н. Алгебра и начала анализа. Ч. ІІ. – М., 1978.
- Юртин І.І та ін. Практикум з вищої математики. – К., 2006.

про публікацію авторської розробки
Додати розробку