Підбірка вправ з рекомендаціями "Функції та їх властивості в задачах графічного змісту"
Запропоновані вправи можна використовувати, як при вивченні нового матеріалу, так і при закріпленні вивченого; та при перевірці знань учнів. Задачі однієї і тієї самої групи можна застосовувати в різний час і в різних класах.
Кривець О.В.
Функції та їх властивості
в задачах
графічного змісту
9 - 11
Задачі графічного змісту є одним із важливих засобів розвитку геометричної інтуїції учнів, що сприяють більш глибокому вивченню основних понять та теорем математичного аналізу та застосуванню їх на практиці, подоланню формалізму в знаннях учнів. Запропоновані задачі можна використовувати, як при вивченні нового матеріалу, так і при закріпленні вивченого; та при перевірці знань учнів. Задачі однієї і тієї самої групи можна застосовувати в різний час і в різних класах.
І. Функції
Запропоновані вправи можна використовувати під час вивчення теми „Застосування похідної до дослідження функції" в 11 класі та під час вивчення теми „ Функції " в 9 класі. Мета цих вправ - розкрити зміст тих означень, які вводяться для дослідження функції. Усні вправи можна поділити на два типи: вправи за готовими малюнками (пропонуємо учням набір графіків деяких функцій, а учні повинні виділити графіки тих функцій, які відповідають певним властивостям і обґрунтувати свій вибір, опираючись на певне означення або властивість) та вправи, в яких треба схематично зобразити графіки функцій, що володіють наперед заданими властивостями. А вводити в навчальний процес подібні вправи варто таким чином:
1) ввести нове означення;
2) показати означення в дії;
3) сформулювати геометричний зміст нового поняття;
4) вивісити таблицю з графіками і сформулювати завдання - виділити функції з вказаними властивостями;
5) забрати таблиці і сформулювати інше завдання - побудувати графіки функцій, які володіють даними властивостями, та функцій, які ними не володіють.
Якщо учень самостійно зможе побудувати графік функції, яка володіє, або не володіє, певними властивостями, то це буде достатнім свідченням того, що учень розуміє матеріал, а не формально його запам'ятовує.
Зразки вправ
1. На координатній площині ХОУ побудуйте фігуру А так, щоб:
1) А була (не була) графіком деякої функції у= f(х);
2) А була (не була) графіком функції х = g(у);
3) А була (не була) одночасно і графіком функції у=f(х), і графіком функції х = g(у).
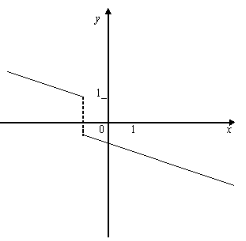
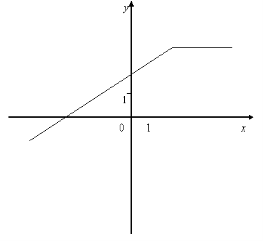
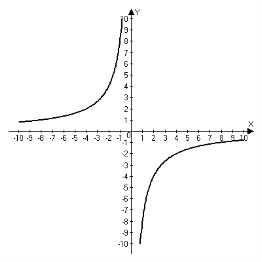
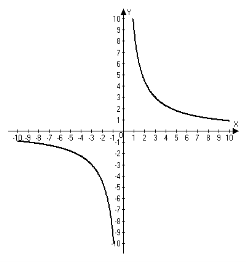
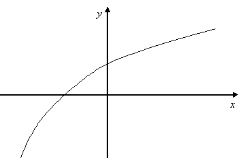
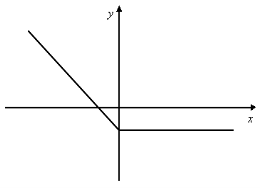
2. Для функцій, графіки яких зображено на мал.1-2, вкажіть область визначення D(х), та область значень Е(у).
3. На осях Ох та Оу дано відрізки [а; в] та [с;d] відповідно. Зобразіть графік функції f(х), для якої D(х) == (а;в], Е(у)=[с;d].
4. Серед функцій, зображених на мал.1-2, знайдіть функції, які:
1) є зростаючими на D(х);
2) є спадними на D(х);
3) не є монотонними на D(х);
вкажіть для них проміжки зростання та спадання.
5. Зобразіть графічно функцію f(х), яка:
1) зростає на D(х);
2) спадає на D(х);
3) не є монотонною на D(х);
4) зростає на D(х) і f(х)<0 на D(х);
5) спадає на D(х) і f(х)>0 на D(х).

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()


![]()
![]()

6. Серед функцій, графіки яких зображені на мал. 3, знайдіть:
1) парні функції;
2) непарні функції;
3) ні парні, ні непарні функції.
Свій вибір обґрунтуйте, опираючись на відповідне означення.
7. Зобразіть графічно функцію f(х), яка є:
1) парною;
2) непарною;
3) ні парною, ні непарною.
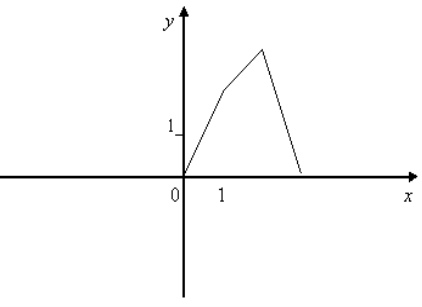
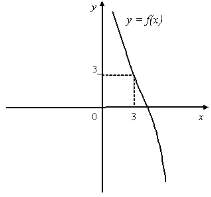
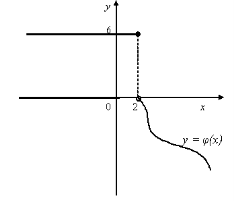
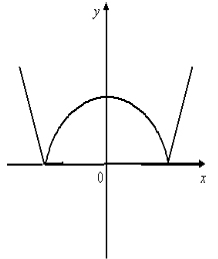
8. На мал.4 зображено частину графіка функції f(х). Добудуєте для х>0 графік функції f(х), якщо:
1) f(х)- парна функція;
2) f(х) - непарна функція;
3) f(х) - ні парна, ні непарна функція.
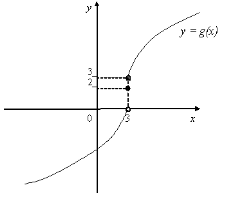
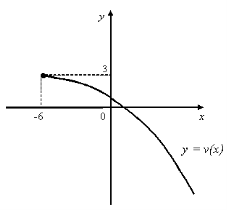
9. На мал.5 зображено частину графіка функції f(х). Добудуйте для х<0 графік функції f(х), якщо:
1) f(х) - парна функція;
2) f(х) - непарна функція;
3) f(х) - ні парна, ні непарна функція.
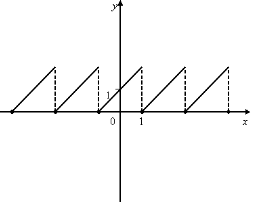
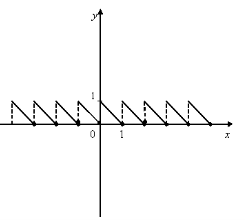
10. На мал.6 зображено частину графіка функції f(х). Відомо, що функція f(х) - періодична з найменшим додатнім періодом, що дорівнює 3. Добудуйте графік функції на всій числовій осі.
11.Зобразіть графічно періодичні функції з найменшими додатними періодами, що відповідно дорівнюють числам 1,5; 4; π; 2π.
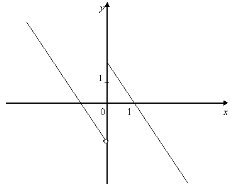
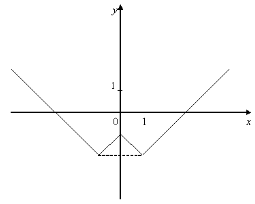
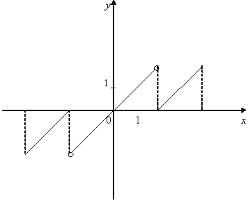
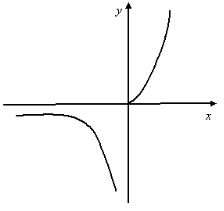
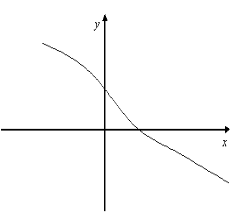
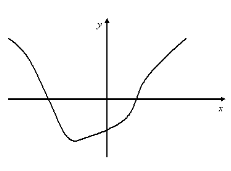
12. Серед функції, графіки яких зображено на мал. 7, знайдіть функції, для яких існують обернені.
![]()
![]()

![]()
![]()

![]()
![]()


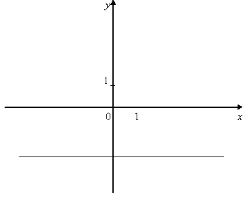


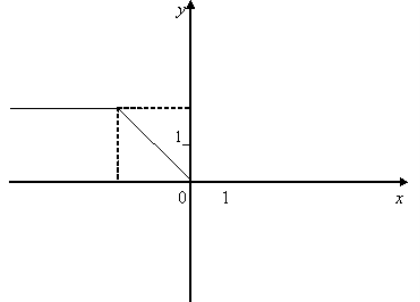


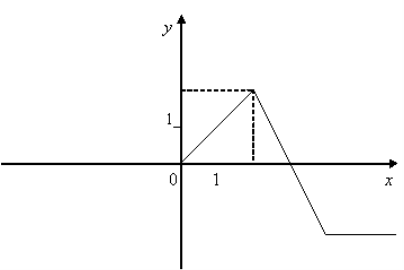


12. На мал. зображено графіки функцій. Знайдіть серед функцій:
1) періодичні;
2) неперіодичні.
Назвіть їх найменший додатній період. Відповідь обґрунтуйте.
14. На осях Ох та Оу дано відповідно відрізки [а; в] та [с; d]. Зобразіть оборотну функцію у=f(х), для якої D(х)= [а; в]; Е(у)= [с; d].

![]()
![]()
![]()
![]()
![]()

II. Границя функції. Неперервність.
З поняттям границі функції учні вперше зустрічаються при вивченні теми,, Похідна" в 11 класі. При поясненні суті змісту поняття границі корисно використовувати задачі графічного змісту: на інтуїтивно - наочному рівні вони допомагають розкрити зміст рівності limf(х)=L, і, зокрема, зміст рівності limf(х)= f(а), знаходити за графіком границю функції в заданій точці, а також визначати точки, в яких функція не має границі.
Зразки вправ
1. За графіками функцій у = х - 3, у = х3, у = х2, у = ![]() , y = tg x,
, y = tg x,
y = ctg x, y = sin x, у=соs х визначте, чи має кожна з них границю в точках х = 0, х = 1, х = -1, і, якщо має, то чому вона дорівнює. Зазначте, які з даних функцій є неперервними в цих точках.
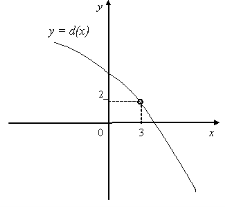
2. На мал. 8 зображено графіки функцій. Визначте для кожної функції, чи має вона границю в точці х = 3(мал. а)-г)), а якщо має, то чому вона дорівнює.
3. Зобразіть графік функції y = f(х), якщо вона задовольняє одну з умов:
1) f(х) визначена в точці х = 2, але не має границі в цій точці;
2) f(х) не визначена в точці х = 2, але має границю в цій точці;
3) f(х) визначена в точці х = 2, має границю в цій точці, але 1іmf(х) ![]() f(2).
f(2).
4. Зобразіть графічно функцію f(х), щоб:
1) f(х) мала границю в точці х = 3;
2) f(х) не мала границі в точці х = 3.
5. Зобразіть графік функції f(х), яка:
1) є неперервною на D(х);
2) не є неперервною на D(х) (має 1-2 точки розриву).
6. Зобразіть графік функції f(х) яка:
1) неперервна в точці х = 1 і f(1)=2;
2) має границю в точці х = 2, але не є неперервною в цій точці;
3) не має границі в точці х = 3.
![]()
![]()


![]()
![]()
![]()
![]()

III. Похідна
У шкільному курсі алгебри та початків аналізу вивчення похідної починається зі встановлення її геометричного змісту. Похідною функції f(х) в точці хо називають кутовий коефіцієнт дотичної до графіка функції в точці (хо; f(хо)). А для того, щоб функція f(х) мала в точці хо похідну (була диференційована в точці хо), необхідно і достатньо, щоб існувала дотична до графіка функції в точці (хо; f(хо)) (непаралельна осі Оу). І лише після цього вводиться загальне означення похідної за допомогою граничного переходу.
Зразки вправ
Вправи 1-5 призначені для усної та письмової роботи в класі під час вивчення геометричного змісту похідної. За графіком функції необхідно знайти наближене значення похідної в зазначених точках або, навпаки, побудувати графік функції, що володіє певними, наперед заданими, властивостями.
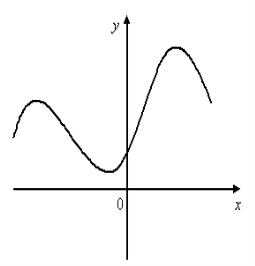
1. За графіком функції f(х) (мал. 9) знайдіть наближене значення похідної f′(х) в точках х = -3; 0; 1; 4; 6.
2. Зобразіть схематично графік функції f(х), що задовольняє умови:
1) f(0) і f′(0) = 1;
2) f(2) = 0 і f '(2) = 1;
3) f(1) = 1 f′(1) = 0.



3. Користуючись графіками функцій (мал.11), вкажіть точки, в яких функція недиференційована (не має похідної).
4. Побудуйте графік функції f(х), що має похідну на всій області визначення, крім точки х = 2.
5. Побудуйте графік функції f(х), що є диференційо- ваною в усіх точках числової прямої, крім х =-2, 0, 5.
Вправи 6-13 призначені для усної та письмової роботи при вивчені теми "Дослідження функції".
6. На мал. 11 зображено графіки деяких функцій. Покажіть для цих функцій:
1) критичні точки;
2) точки максимуму;
3) точки мінімуму.
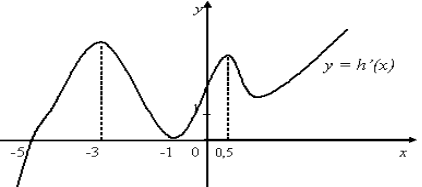
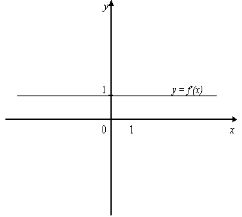
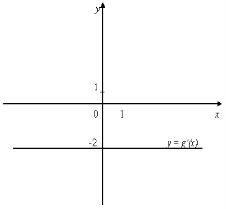
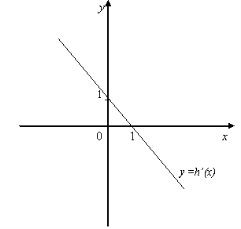
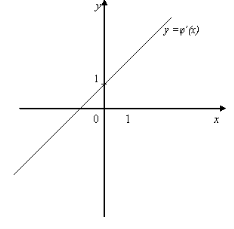
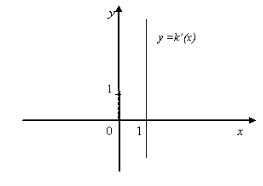
7. На мал. 12 зображено графіки похідних деяких функцій. Визначте для цих функцій:
1) критичні точки;
2) точки максимуму;
3) точки мінімуму;
4) проміжки зростання;
5) проміжки спадання.
8. На осі Ох задано відрізок [а; в], що є областю визначення функції f (х). Зобразіть графік функції f(х), що володіє такими властивостями:
1) функція f(х) має на [а; в] найбільше (найменше) значення, що співпадає з максимумом (мінімумом) функції;
2) функція f(х) має на [а; в] екстремум (2-3 екстремуми);
3) функція f(х) має екстремум в точці хоє [а; в], але не має похідної в цій точці;
4) функція f(х) не має на [а; в] найбільшого (найменшого) значення.
9. Визначаючи точки мінімуму функції у = h(х) за графіком її похідної (мал.10), учень назвав точки х = 3 та х = 1. Чи правильна його відповідь? Чому?
10. Визначаючи точки максимуму функції h(х) за графіком її похідної (мал. 10), учень назвав точку -5. Чи правильна його відповідь? Чому?
11. Побудуйте схематично графік функції f(х), яка задовольняє умови:
1) f′(х) = 1 для х є D(х);
2) f′(х) = -1для х є D(х);
3) f′(х) = 0 для х є D(х);
4) f′(х) > 0 для х є D(х);
5) f′(х) < 0 для х є D(х);
6) f′(х) > 0 при х<4 і f′(х) < 0 при х>4;
7) f′(х) < 0 при х<4 і f'(х)>0 при х>4.
12. Зобразіть схематично графік функції f(х), похідна якої міняє знак зліва направо за такою схемою +-+-+
13. Функції f(х) та g(х) володіють однією з властивостей:
1) f(а) ![]() g(a) і f′(a)= g′(a);
g(a) і f′(a)= g′(a);
2) f(a)= g(a) і f′(a) ![]() g′(a);
g′(a);
Поясніть геометричний зміст цих властивостей та зобразіть схематично на графіку.



![]()
![]()

![]()
![]()




ІІІІ. Логарифмічна, показникова та степенева функції.
При вивченні логарифмічної, показникової та степеневої функцій, для кращого усвідомлення учнями властивостей цих функцій та їх графіків, доцільно пропонувати вправи на встановлення відповідності між функціями та наперед побудованими графіками. Подібні вправи не займають багато часу на уроці (особливо за умови, що графіки функцій зображені на окремих аркушах паперу, а на інших аркушах записані формули функцій, для яких треба відшукати відповідні графіки), але сприяють кращому засвоєнню учнями теоретичного матеріалу, розвитку логічного мислення.
Зразки вправ
1. На мал. 13 подано графіки функцій: .-
1) у=х -6 ; 2) у = х-3; 3) y = x0.2 ; 4) у = х![]() Встановіть відповідність між графіками і функціями, та опишіть властивості кожної функції.
Встановіть відповідність між графіками і функціями, та опишіть властивості кожної функції.
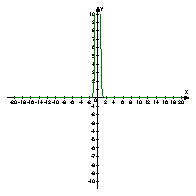
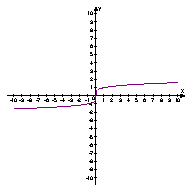
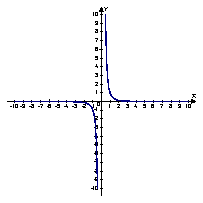
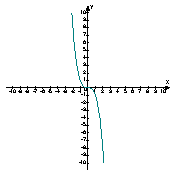
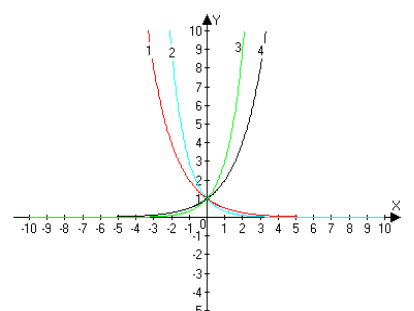
2. На мал. 14 подано графіки функцій:
1) у = 2x; 2) у = 3x; 3) y = ![]() ; 4) у =
; 4) у = ![]()
Встановіть відповідність між графіками і функціями.
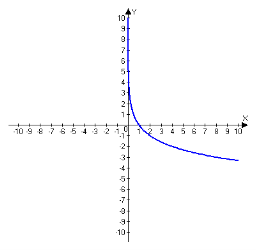
3. На мал. 16 схематично зображено графіки функцій:
1) y = log2x; 2) у = ![]() ; 3) y = log3 (x); 4) y =
; 3) y = log3 (x); 4) y = ![]() x)/
x)/
Встановіть відповідність між функціями та графіками.
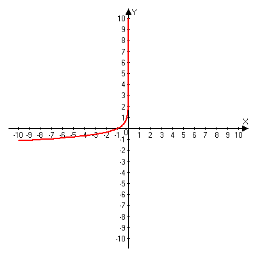
4. Графік якої з функцій:
1) у = аx, 0<а<1; 4) у = аx + 1, 0<а<1;
2) у = аx - 1, 0<а<1; 5) у = аx - 1 а>1;
3) у = аx-1, 0<а<1; 6) у = аx-1, а<1
зображено на мал. 15?
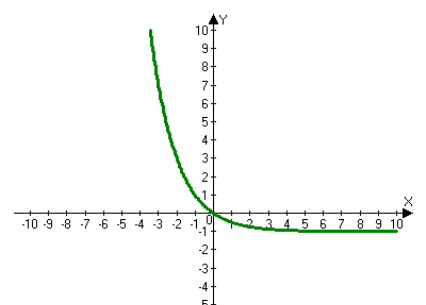
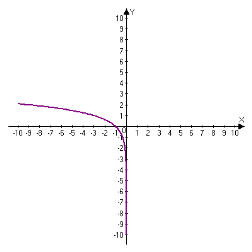
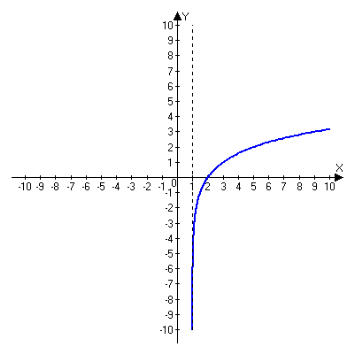
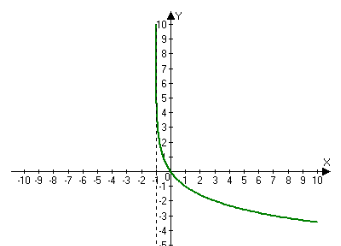
5. На мал. 17 схематично зображено графіки двох із шести функцій:
1) у = 1оga x, 0<а<1; 4) ) у = 1оga x , а>1;
2) у = 1оga (x + 1), 0<а<1; 5) у = 1оga (x + 1), а>1;
3) у = 1оga (x – 1), 0<а<1; 6) ) у = 1оga (х - 1), а>1.
Яких саме?
6. Які з функцій є зростаючими, а які спадними:
1) у = 1оg3 x; 3) у = 1оg0.5 x; 5) у = 1оgsin30ºx.
2) у = 1g x; 4) у = 1оgπ x;
7. Які з поданих функцій є зростаючими, а які спадними:
1) у = 5x; 3) у = 0,1x; 5) y = 36-x;
2) у = ![]() ; 4) у = πx; 6) y =
; 4) у = πx; 6) y = ![]() .
.






 а) б)
а) б)

в) г)



1


про публікацію авторської розробки
Додати розробку
