Похідна та її застосування

Конспект уроку з алгебри в 11 класі: «Похідна та її застосування»

Мета: удосконалити вміння та навички учнів розв’язувати задачі на застосування похідної, продовжити підготовку до зовнішнього незалежного тестування; розвивати пізнавальний інтерес, навички роботи з тестами, логічне мислення; виховувати працьовитість, зібраність, організованість, старанність, відповідальність та вимогливість до себе.

Тип уроку: удосконалення знань, умінь та навичок

Обладнання: комп’ютерний клас, програма-тренажер «Похідна», картки з тестами, рисунки з графіками функцій.

Завантажити програму тренажер

«Недостатньо лише мати гарний розум, Головне – це добре застосовувати його»

                                                                                                            Р. Декарт

Хід уроку

І. Організаційний момент.

Привітання, перевірка готовності до уроку. Налаштування на робочу обстановку.

ІІ. Мотивація навчальної діяльності. Оголошення теми та завдань уроку.

На попередніх уроках ви засвоїли одне із фундаментальних понять алгебри та початків аналізу – похідну. ЇЇ появі ми завдячуємо таким вченим, як П.Ферма, І.Ньютон, Г.Лейбніц, Ж.Лагранж.

Поняття похідної широко застосовується у механіці, військовій справі, медицині, космонавтиці, фізиці, астрономії. Тому і приділяється така увага цьому поняттю.

Р. Декарт говорив: «Недостатньо лише мати гарний розум, головне – це добре застосовувати його». Темою уроку є «Розв’язування вправ з теми «Похідна та її застосування»». Основна мета нашого уроку – використання теоретичних знань при розв’язанні практичних задач. Ключова ціль – впевнено себе почувати під час ДПА та ЗНО, де досить прості в розв’язанні задачі мають достатньо нестандартний зміст.

ІІІ. Актуалізація опорних знань

Фронтальне опитування за технологією «Мікрофон»

1. Дати означення похідної?

Число, яке дорівнює границі відношення приросту функції до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля

2. Що таке похідна з механічної  точки зору? S`(t) = V(t);  V`(t)=а(t)

3. В чому полягає геометричний зміст похідної.

Рівняння дотичної

Якщо функція в деякій точці х₀ має похідну, то в цій точці визначено дотичну до графіка функції, при чому її кутовий коефіцієнт дорівнює f`(x₀).

Рівняння дотичної y= f/(x₀)(x-x₀) + f(x₀)

4. Сформулюйте правила диференціювання 

5. Ознака зростання функції Якщо для всіх x з деякого проміжку f`(x) > 0 то функція зростає на цьому проміжку

6. Ознака спадання функції Якщо для всіх x з деякого проміжку f`(x) < 0 то функція спадає на цьому проміжки

7. Назвіть ознаку точки максимуму функції Якщо при переході через точку x₀  похідна змінює знак з плюса на мінус, то x₀  – точка максимуму

8. Ознака точки мінімуму функції Якщо при переході через точку x0  похідна змінює знак з мінуса на плюс, то x₀  – точка мінімуму

9. Які точки можуть бути екстремальними? Якщо точка x₀  є точкою екстремуму функцій то f`(x) = 0 або f не є диференційованою в цій точці  її називають критичною.

10. Назвіть етапи алгоритму дослідження функції для побудови її графіка 

Знання таблиці похідних та правил диференціювання – це надійний крок до розв’язання багатьох задач.

Прийом «Лови помилку» (1 учень біля дошки):

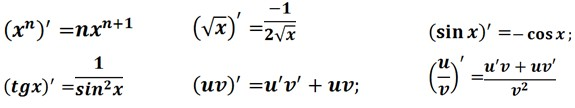
Розв’язування завдань

Прийом «Чи правильно, що…»

Функція зростає на [-7;2) і (2;8] значить вона зростає на [-7;8] (Ні)

Критична точка є точкою екстремуму. (Ні)

Точка екстремуму є критичною (Так)

Точки на графіку x₁=1, x₂=-1, x₃ = 2 є точками максимуму. (Ні)

Графік

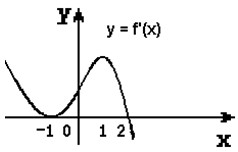
На рисунку зображено графік функції f(х), визначеної на відрізку [-7;7].

Скільки нулів матиме функція f/(х) на проміжку (-7;7)?

графік функції

ІV. Застосування вмінь та навичок

Виконання завдань у форматі ЗНО.

Виконання тестів – надійний шлях до здачі ЗНО

Робота по групах

І група учнів – тестування на комп’ютерах за допомогою програми-тренажера «Похідна». По закінченню програма виставляє оцінку автоматично за 12-бальною системою.

ІІ група – тести на картках

V. Підсумок уроку

         Прийом «Закінчи речення»

Сьогодні на уроці ми…

Найважливішим на уроці для мене було…

Найбільше зацікавило…

Найскладнішим для мене було…

Щоб усунути прогалини в знаннях, я маю…

VІ. Домашнє завдання

Повторити таблицю похідних елементарних функцій.

Підготувати повідомлення про відомих математиків, які зробили значний внесок у розвиток поняття похідної.

Виконати у тесті № 1 «Перевір себе» завдання № 1-18 на стор. 150-152 (Г.П.Бевз, В.Г.Бевз. Математика, 11 – К., Генеза, 2011)