«Поняття динамічної задачі. Розв’язання динамічних задач»

У процесі вивчення геометрії відбувається розвиток логічного та алгоритмічного мислення учнів, почуття точності та математичності мови, здатності чітко висловити думку, формулювати і обґрунтовувати твердження, що дає можливість виховати конкурентоспроможну особистість.

Формуванню творчої самостійності в процесі навчання геометрії можуть сприяти правильно підібрані завдання і різноманітні прийоми з навчання їх розв’язування. Безумовно , не кожна задача сприяє формуванню творчої самостійності школярів. На наш погляд, цьому більшою мірою сприяють динамічні задачі, в яких формулювання задачі в певних умовах здатне наштовхнути учнів на такий вид творчої діяльності , який передбачає висунення гіпотез і їх перевірку.

Знаходження зазначених зв'язків, ми відносимо до такого виду діяльності, як аналіз завдання або розвиток завдання, де під розвитком завдання розуміється отримання таких результатів: нових завдань, методів, висновків тощо.

Наприклад, робота з аналізу вже розв’язаною задачею може включати пошук відповідей на наступні питання:

1. Як можна перевірити результат?

2. Чи можна розв’язати задачу в інший спосіб?

3. Спробуйте скласти обернену задачу.

4. Чи можна сформулювати аналогічну задачу з планіметрії? Якщо так, то сформулюйте і зіставте способи їх розв’язання.

5. Чи можна сформулювати більш загальну (динамічну) задачу?

Слід зазначити , що проводити аналіз або розвиток завдань необхідно як на звичайних уроках, так і на спеціально створених: урок розв’язування однієї задачі, урок розв’язування одним методом, урок розв’язування динамічних задач.

Таким чином, включення в навчання геометрії правильно підібраних завдань і цілеспрямованої роботи з ними, сприятиме формуванню елементів творчої самостійності, що в свою чергу сприяє підвищенню якості математичної підготовки учнів, зміни їх відносини до геометричних знань, усвідомлення своїх можливостей у цій галузі і подолання страху перед завданнями, запропонованими в ДПА і ЗНО.

Приклад розробки уроку введення динамічної задачі в шкільному курсі планіметрії.

Урок - лекція на тему: «Поняття динамічної задачі. Розв’язання динамічних задач».

Мета: формування в учнів уміння вирішувати динамічні задачі.

Завдання:

1) Освітнє : ознайомити з поняттям динамічної задачі; сформувати вміння вирішувати динамічні задачі;

2) Розвивальне : розвиток логічного мислення, пам'яті, розвиток загальнонавчальних умінь;

3)Виховне : виховання працьовитості, взаємодопомоги, математичної культури.

Тип уроку: вивчення нового матеріалу.

Структура уроку:

• організаційний момент - 2 хвилини,
• актуалізація знань і умінь - 5 хвилин,
• пояснення нового матеріалу - 21 хвилин,
• закріплення пройденого матеріалу - 15 хвилин,
• підведення підсумків, завдання додому - 2 хвилини.

Методи навчання: словесні (лекція, бесіда), практично (вправи).

Обладнання: дошка, крейда, конспект, інтерактивна дошка, презентація.

Хід уроку

1. Привітання учнів, відмітка відсутніх, оголошення теми та мети уроку.

2. Актуалізація знань.

Питання:

1. Сформулюйте означення задачі.

2. Яку роль задача має в навчанні геометрії?

3. Які функції виконує задача у навчанні геометрії?

4. Які класифікації задач вам відомі? Назвіть їх.

5. Чи знаєте ви, що являє собою динамічна задача?

6. Сформулюйте визначення динамічної задачі.

3. Пояснення нового матеріалу.

Динамічні задачі займають важливе місце в курсі геометрії. Дана тема багата за змістом, за способами і прийомами розв’язків  динамічних задач, за можливостями її застосування при вивченні ряду інших тем шкільного курсу геометрії. Це пояснюється тим, що широко використовуються в різних розділах геометрії, при розвязуванні важливих прикладних задач.

Означення: Динамічні задачі - задачі, в яких один або декілька з параметрів розглянутої фігури змінюється в певних межах і з'ясовується питання про межі зміни інших параметрів цієї фігури.

Задача 1.

Знайти кути рівнобедреного трикутника (рис 1), якщо один з них дорівнює: а) 110̊ ; б) 70̊.

Розв’язання

а)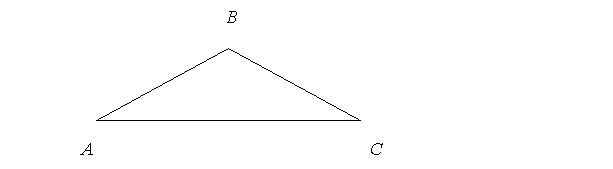                                                                              

Рис. 1

1. Нехай АВС = 110̊ .

Сума кутів трикутника дорівнює 180̊. У рівнобедреного трикутника кути при основі рівні. Отже, ВАС = ВСА = (180̊  - 110̊ )/2 = 45º

2. Нехай ВАС = 110̊ .

Звідси слідує що ВСА = ВАС = 110̊ (як кути при основі). Що суперечить так як сума кутів трикутника повинна дорівнювати 180̊ .

б) 1. Нехай АВС = 70̊ .

ВАС = ВСА = (180̊  - 80̊ )/2 = 55º .

2. Нехай ВАС = 70̊ .

Звідси слідує що ВСА = ВАС = 70̊ (як кути при основі).

АВС = 180̊ – (70̊  + 70̊) = 40̊  .

Відповідь: кути трикутника дорівнюють: а) 110̊, 45º, 45º ;

б) 70̊, 55º, 55º або 70̊, 70̊, 40̊.

Задача 2.

Чи рівні рівнобедрені трикутнику на рисунку 2 за висотою до бічної сторони та кутом, який утворює ця висота з бічною стороною?

Розв’язання

Трикутники  АВС і А1В1С1  – рівнобедрені, АВ = ВС, А1В1=В1С1,  АD = А1D1, але один з них гострокутний, а другий – тупокутний.

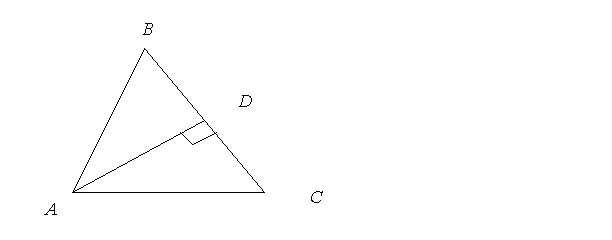
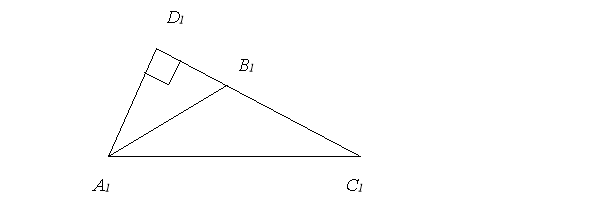
Рис. 2

Відповідь: Ні.

Задача 3.

Знайти кути рівнобедреного трикутника, якщо один з них дорівнює α.

Розв’язання

Кут α може бути як кутом при основі рівнобедреного трикутника, так і кутом при вершині. При цьому слід враховувати, що кут при основі рівнобедреного трикутника може бути тільки гострим. Розглянемо можливі випадки:

1. α < 90̊. Значить, α може бути як кутом при основі, так і кутом при вершині рівнобедреного трикутника. Для першого випадку кути трикутника α, α,180̊ - 2α, для другого – α, 90̊ - α/2, 90̊ - α/2.

2. α ≥  90◦. У цьому випадку α може бути тільки кутом при вершині, і кути трикутника дорівнюють α, 90̊ - α/2, 90̊ - α/2.

Відповідь: якщо α < 90◦, то кути трикутника дорівнюють α, α,180̊ -2α або α, 90̊-α/2, 90̊-α/2. Якщо α ≥  90̊, то кути трикутника дорівнюють α, 90̊ – α/2, 90̊ – α/2.

4. Закріплення матеріалу.

Методичні рекомендації щодо розв’язання  задачі:

Для розв’язання  даної задачі необхідно знати, перш за все, що таке коло, півколо, діаметр, прямокутний трикутник, катети, гіпотенуза, медіана, властивості медіани. Так само для розв’язання  задачі другим способом, тобто з залученням алгебри, необхідно знати теорему Піфагора.

5. Творче завдання додому: дітям дається завдання у вигляді динамічної задачі, яке вони виконують у парах, аналізують задачу, виконують креслення, виявляють кілька способів розв’язання.

У результаті виконання завдання відпрацьовуються вміння аналізувати умову задачі, правильність побудови малюнка, логічне мислення. Робота вчителя повинна бути спрямована на те, щоб учні усвідомили, що якщо в задачі точно не визначено особливості геометричної конструкції, то для повного розв’язку  такої завдачі необхідно розглянути всі можливі випадки взаємного розташування елементів конструкції та інших її особливостей . На початкових етапах знайомства з такими задачами, коли учні ще не мають достатнього запасу прийомів вирішення подібних задач, представляється важливим навчання розгляду різних ситуацій , виявлення істотних фактів, що впливають на конкретну геометричну ситуацію.

Систематична організація подібної роботи сприятиме розвитку конструктивного мислення і такого компонента творчого мислення як гнучкість.

Так як у шкільному курсі геометрії динамічних завдань немає, наочний розв’язок  таких задач можна використовувати для вивчення або закріплення нового матеріалу. Задачу, розв’язану  першим способом, необхідно розглянути при вивченні прямокутного трикутника, його елементів (7 клас). Задачу, розв’язану другим способом, необхідно розглянути при вивченні теореми Піфагора (8 клас). Так само можна підібрати ряд задач для самостійного дослідження, з метою більш глибокого розуміння методів розв'язання динамічних задач або розробити факультативний курс.

Викладання геометрії не може обійтися без наочності. У тісному зв'язку з наочністю навчання і його практичність. Адже саме з життя ми черпаємо конкретний матеріал для формування наочних геометричних уявлень, роблячи навчання узгодженим із життям дитини, його досвідом. Процес навчання спрощується при розумному використанні принципу наочності. Навчання не повинно бути перенасичене ілюстраціями, схемами, таблицями та іншими формами наочності, але в деяких важкодоступних питаннях застосування наочності необхідно. І саме використання засобів мультимедії дозволяє вчителю урізноманітнити урок новими видами діяльності, наситити його наочною інформацією, підвищити мотивацію учнів, інтерес до предмета.