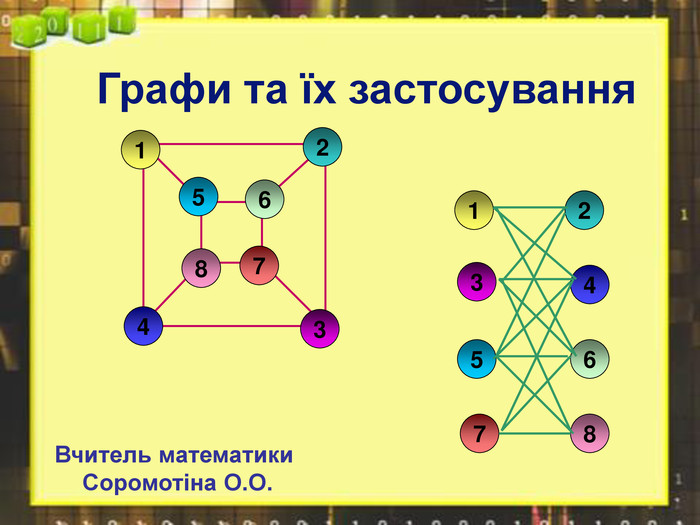
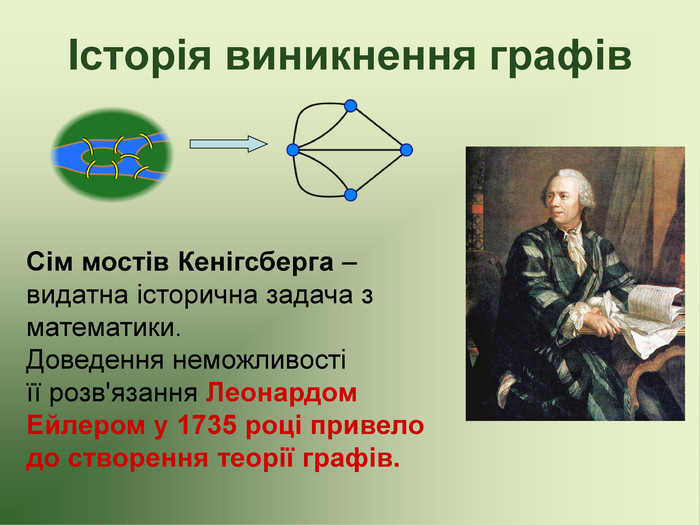
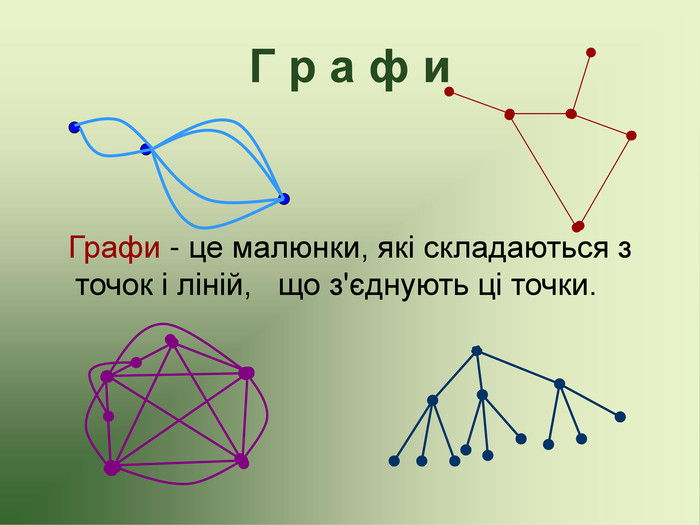
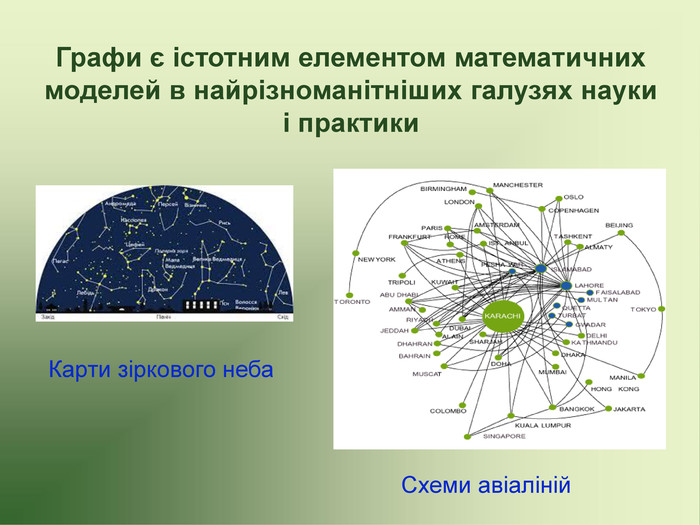
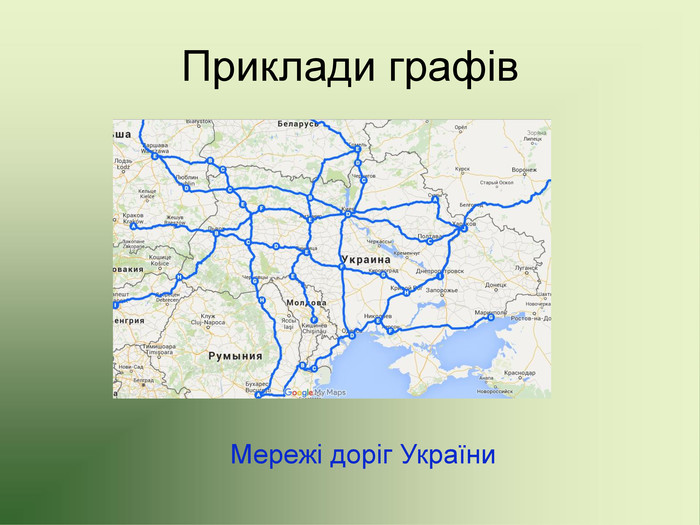
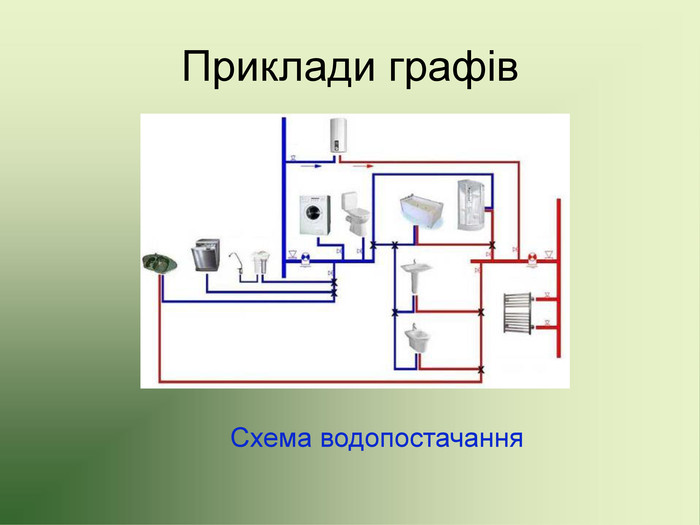
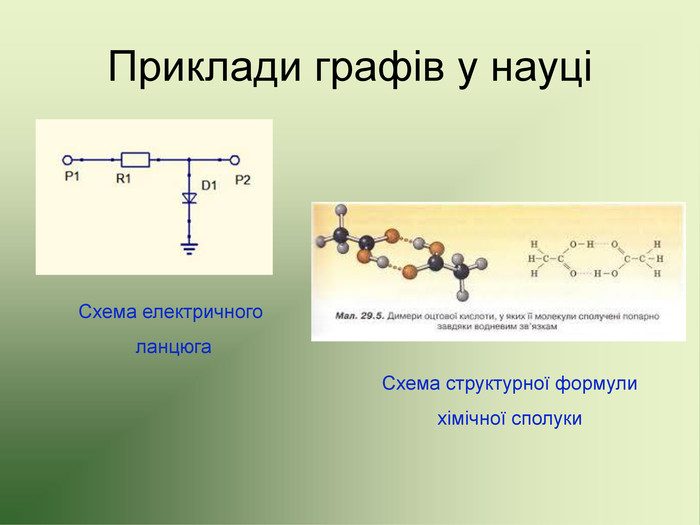
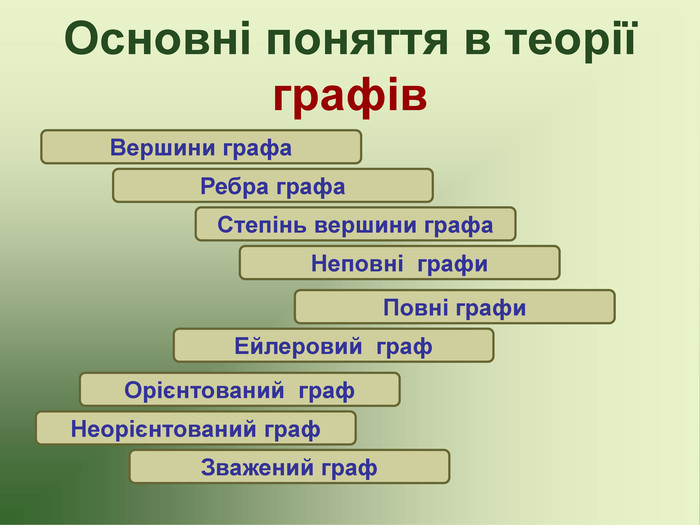
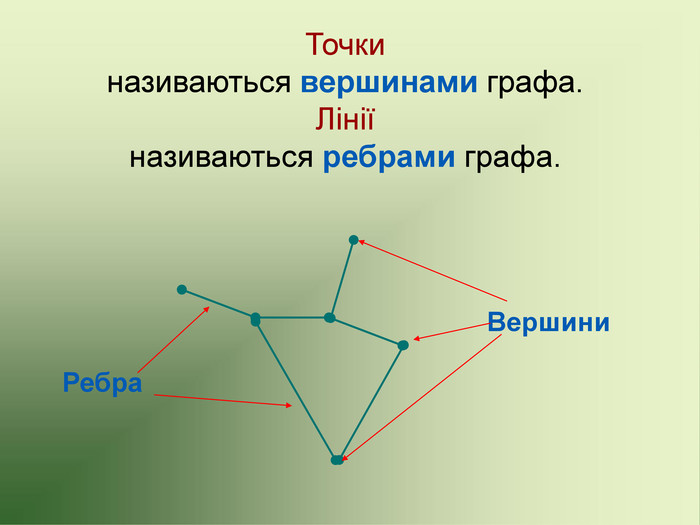
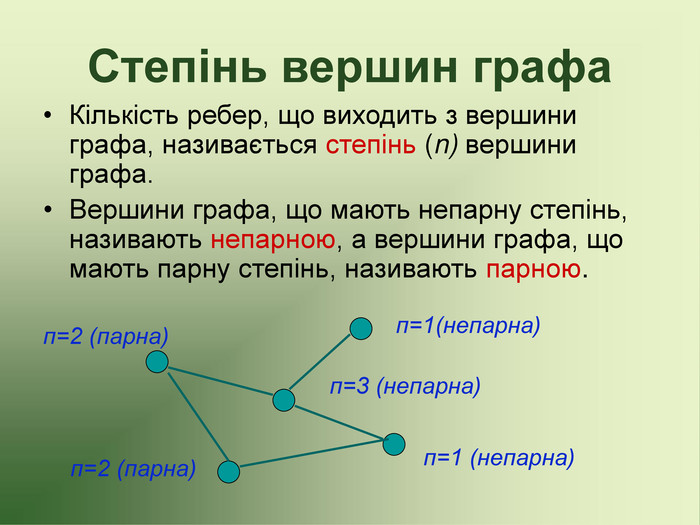
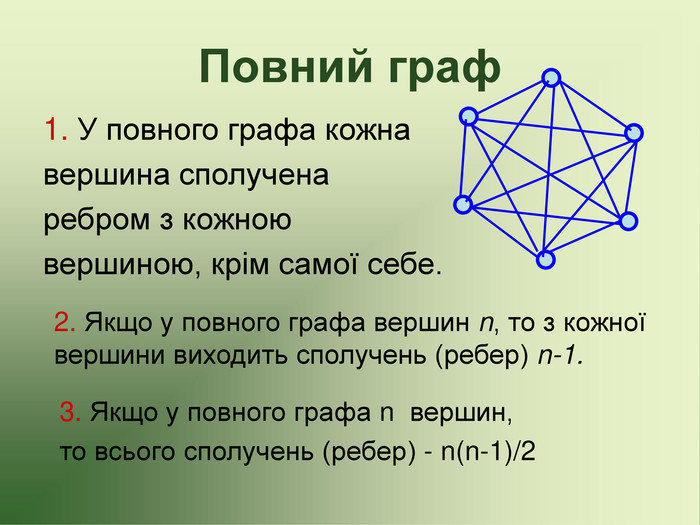
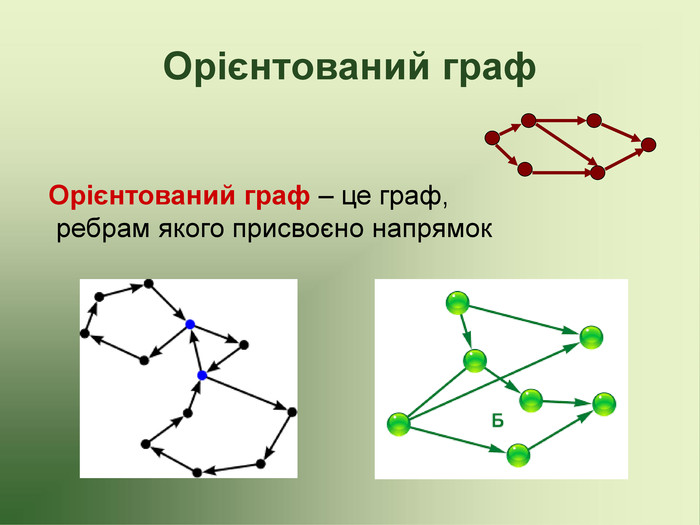
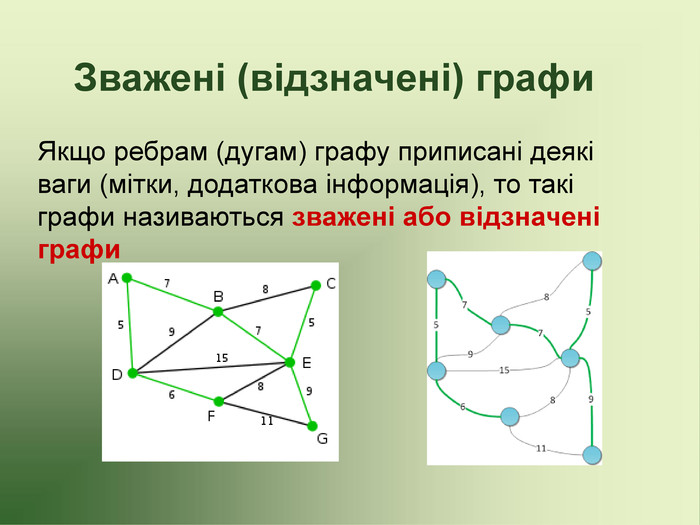
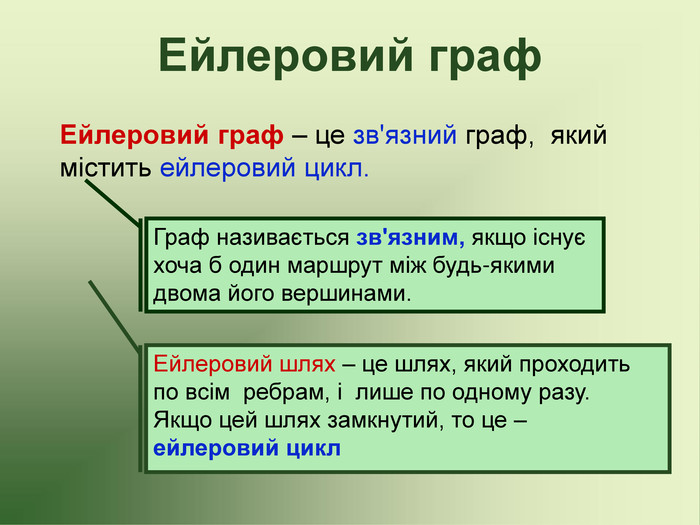
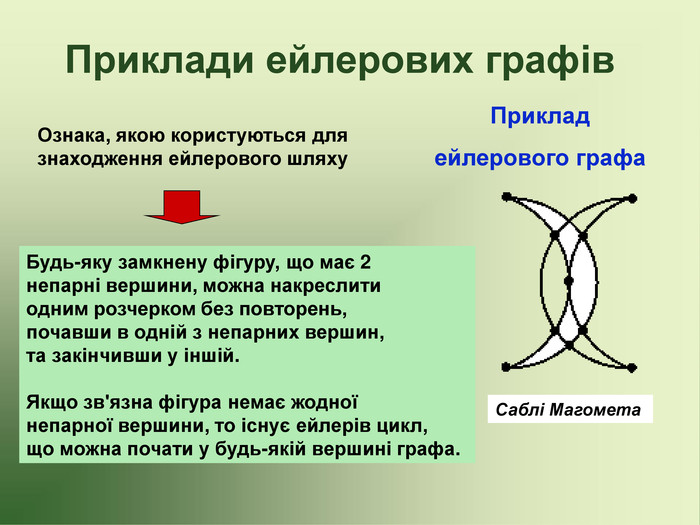
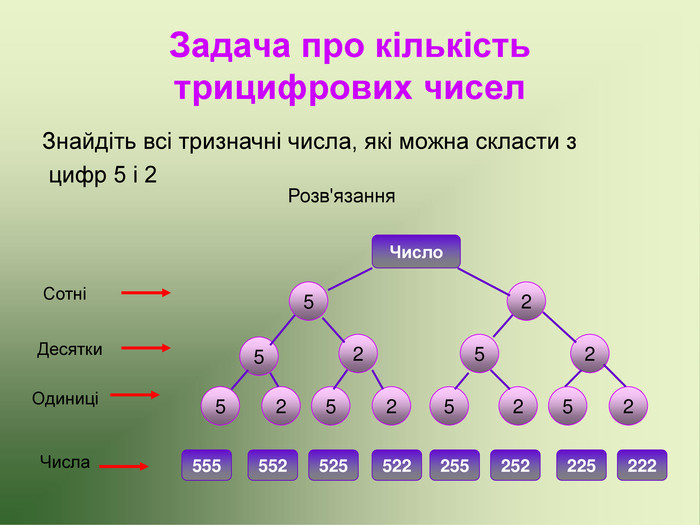
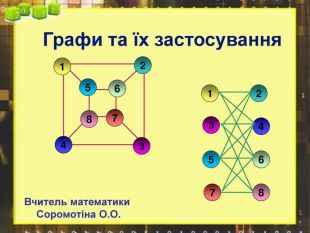
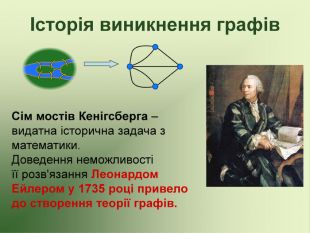
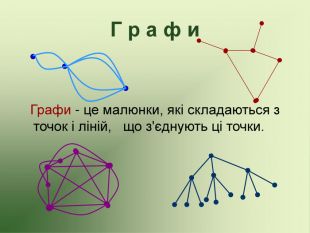
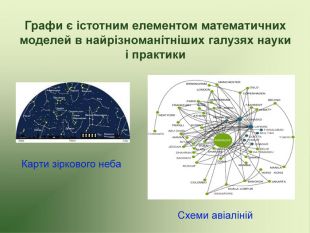
Презентація до факультативу з математики "Графи"
Про матеріал
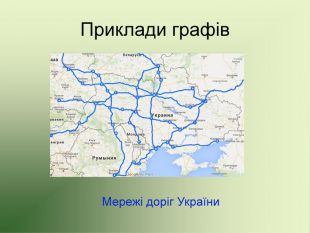
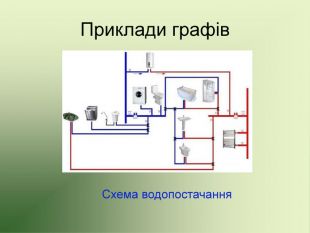
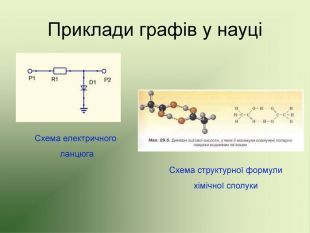
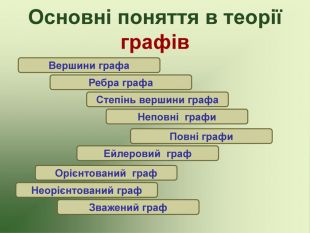
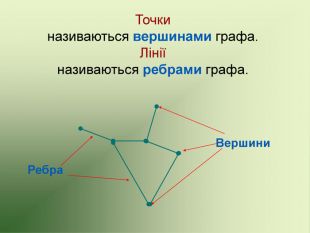
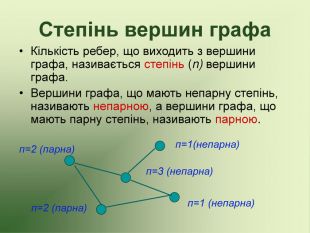
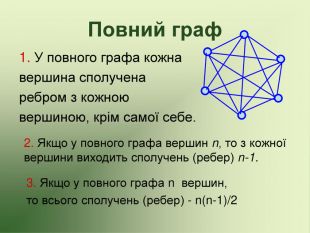
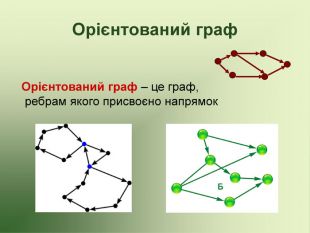
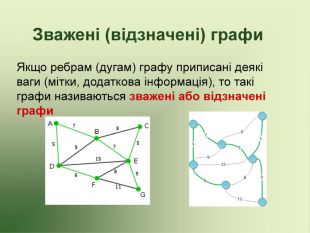
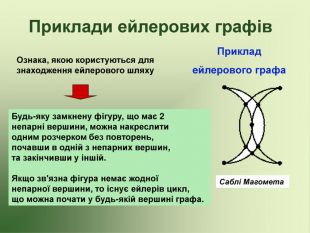
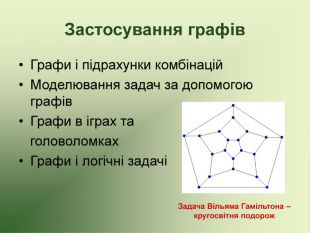
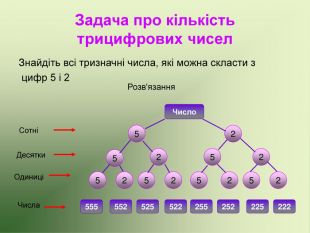
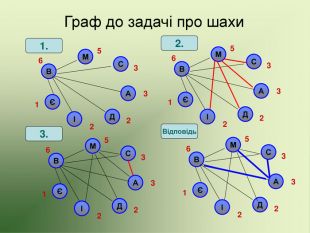
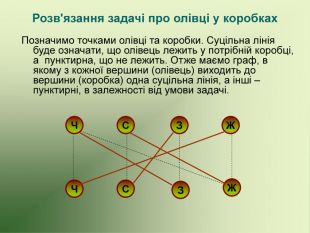
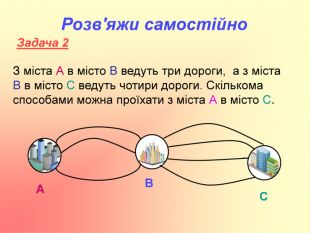
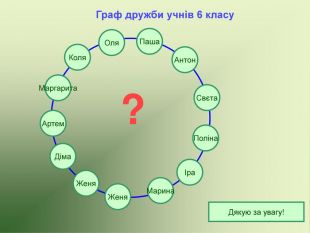
Презентація використовується на факультативних заняттях з математики за темою "Цікава математика". В презентації розміщено теоретичний матеріал за темою "Графи" та цікаві задачі, які можна розв'язувати за допомогою графів.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку