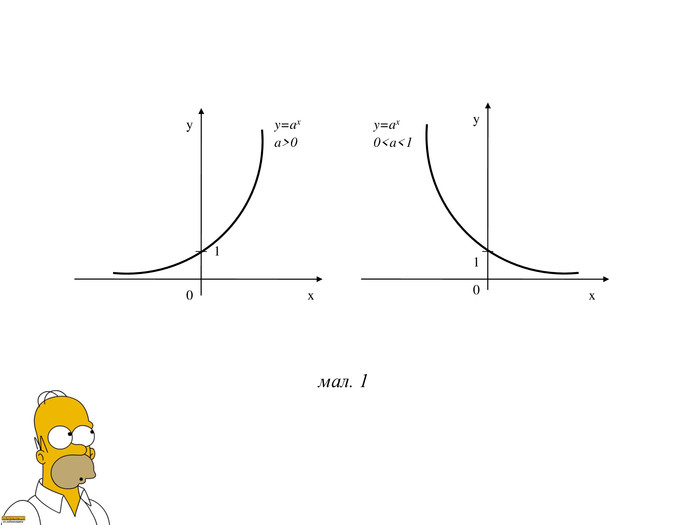
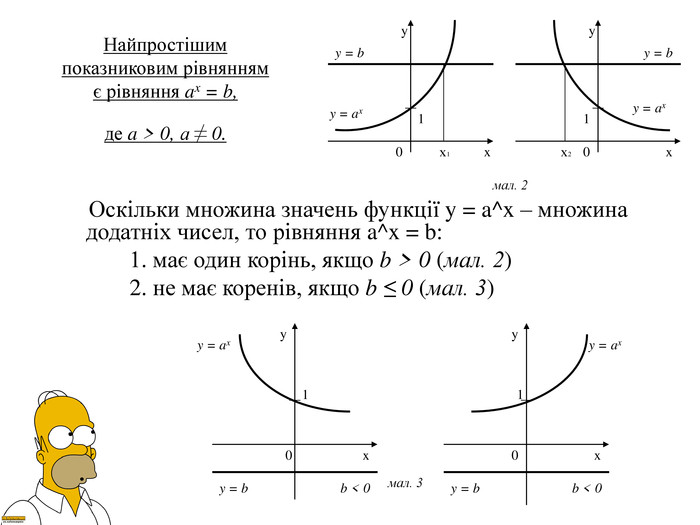
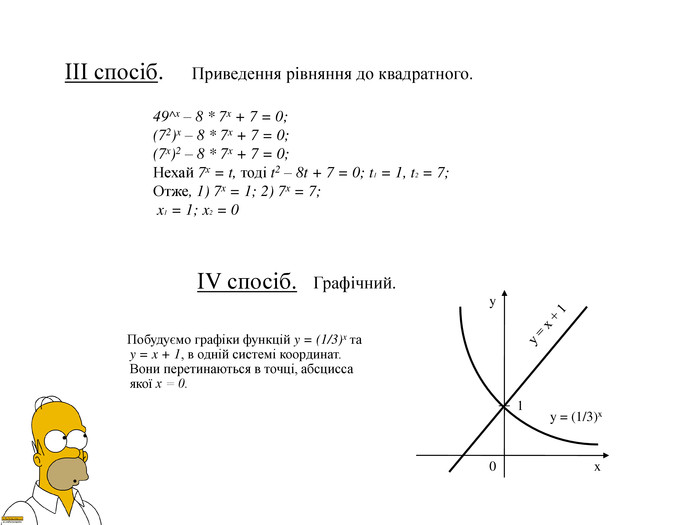
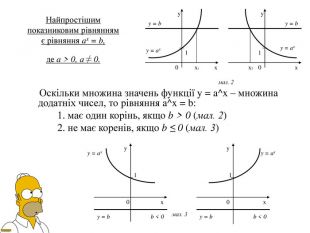
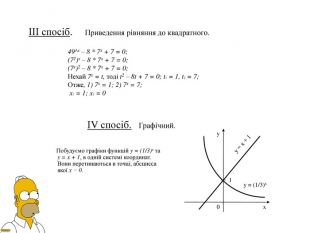
Презентація Показникова функція
Про матеріал
Дає вчителю можливість систематизувати матеріал з даної теми та використовувати при вивченні теми. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку