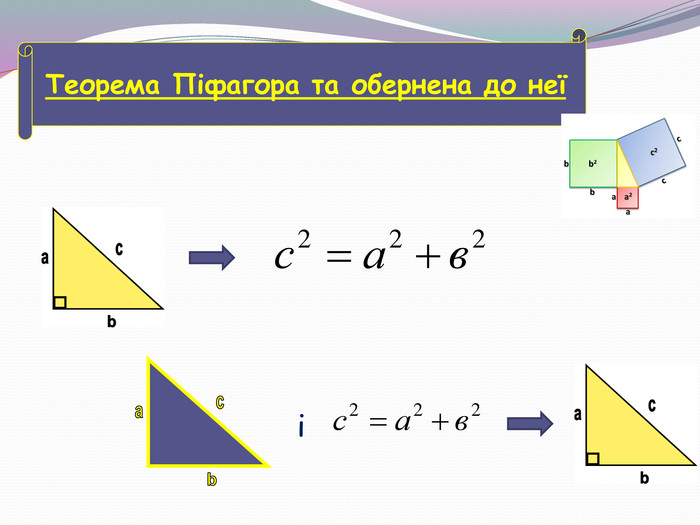
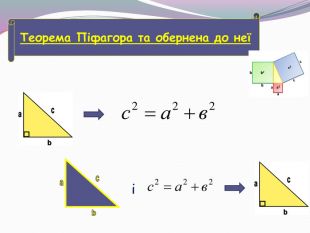
Презентація "Теорема Піфагора (2 урок)"
Про матеріал
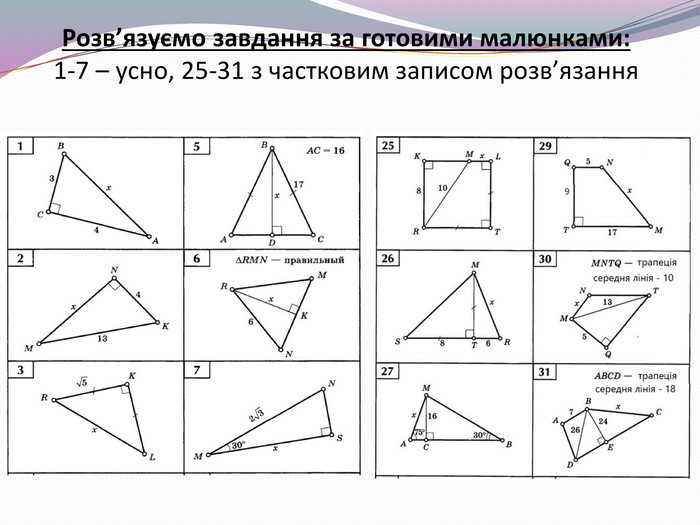
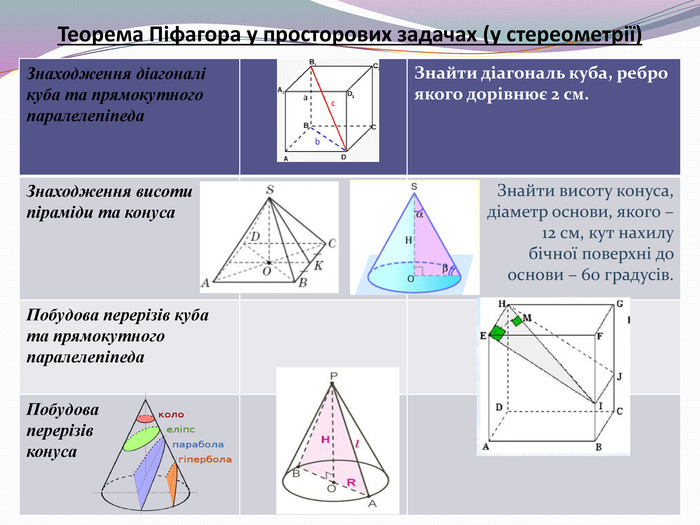
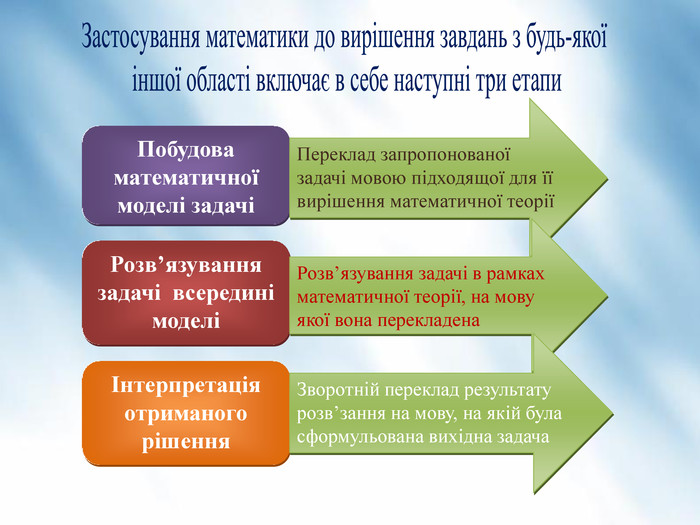
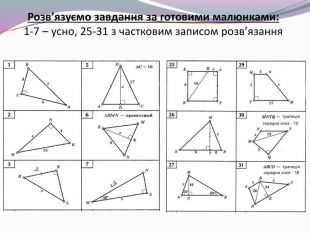
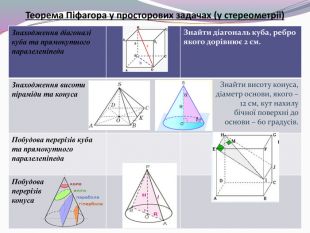
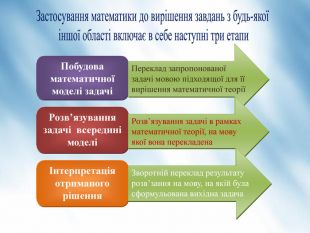
Презентація до другого уроку теми "Теорема Піфагора". На уроці розв'язуємо задачі, а також учні отримують завдання Проєкту "Практичне використання теореми Піфагора у будівництві (техніці, навігації)". Вчитель на прикладі: "Теорема Піфагора у просторових задачах (стереометрії)" демонструє один із напрямків використання в подальшому матеріалу, що вивчається, акцентує увагу на складанні математичної моделі прикладної задачі. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку