ПРИКЛАДНІ ЗАДАЧІ ДО ТЕМ : «ТЕОРЕМА СИНУСІВ , ТЕОРЕМА КОСИНУСІВ»

ПРИКЛАДНІ ЗАДАЧІ ДО ТЕМ : «ТЕОРЕМА СИНУСІВ , ТЕОРЕМА КОСИНУСІВ»

Задача 1. Два теплоходи починають рухатися одночасно з одного й того самого пункту рівномірно прямими, що перетинаються під кутом ϕ. Швидкість першого теплохода становить a км/год, другого – b км/год. Знайдіть відстань між теплоходами через t годин.

Розв’язання. З трикутника ABC за теоремою косинусів знаходимо шукану відстань:

BC² = AB² + AC² – 2AB AC cosϕ = (at)² + (bt)² – 2abt² cosϕ,

звідси

BC = t(a² + b² – 2ab cosϕ).

Відповідь. t(a² + b² – 2ab cosϕ)

 Задача 2. О 7 годині ранку пасажирський літак вилетів з міста A. Прибувши до міста B, літак зробив зупинку на 30 хвилин, після чого о 8 годині 10 хвилин повернув на 35° і о 9 годині здійснив посадку в місті C. Знайдіть відстань між містами A і C, якщо середня швидкість літака протягом усього польоту дорівнювала 320 км/год.

Розв’язання. За умовою літак з міста A до міста B  долетів за год, отже, відстань між містами приблизно дорівнює 213,3 км. Від міста B до міста C літак летів протягом год, отже відстань між цими містами приблизно становить 266,6 км.

= 35°,

звідси випливає, що .

 За теоремою косинусів маємо: 

AC = (AB² + BC² – 2AB BC cos145°) 458 км.

 Відповідь. 458 км

Задача №3

Для знаходження відстані від  точки А до дзвіниці В, яка розташована на іншому березі річки, за допомогою віх, рулетки і приладу для вимірювання кутів (теодоліту) позначили на місцевості точку С таку, що ВАС= 42°, кут АСВ=64° , АС= 20м. Знайдіть відстань від А до В.

Відповідь: 18,8см.

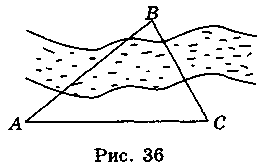
Задача №2

Потрібно знайти висоту схилу, вздовж якого дуже небезпечно підніматись.

Для цього беруть дві точки перед схилом (точки D і С), вимірюють між ними відстань, а потім теодолітом вимірюють кути АDB і ACB (див малюнок). Залишається знайти АВ.

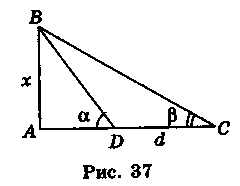
Дано: DC=12м, ACB =44°, ADB=63°.

Знайти: АВ

Розв’язання

BDC=180° - ADB =117°.

CВD=180° -BDC - ACB =19°.  

З  трикутника BDC за теоремою синусів

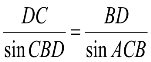
BD=25,6 м.

З трикутника ABD за означенням синуса прямокутного трикутника

sinADB=    AB22,7м.

Відповідь: 22,7м.

Задача №3

Зараз ми розглянемо, як шукають відстані до планет та найближчих зір. Для цього одночасно спостерігають за космічним тілом з різних точок на планеті (А і В). Але спочатку потрібно визначити точну відстань між цими точками, що ми і зробимо з однією неточністю , радіус Землі ми візьмемо наближений, що в реальних умовах недопустимо.

Припустимо, що по поверхні Землі  (по дузі), відстані між пунктами А і В 8000 км, радіус же Землі 6400 км.

1) Знайдемо кут, що відповідає дузі кола в 8000 км. Довжина  дуги до довжини кола відносяться як кут дуги до 360°.

                    AOB72°  

2) Знайдемо інші кути трикутника AOB

OAB=OBA= =54°

3) Знайдемо за теоремою синусів відрізок АВ

АВ=7499км.

4) крім того, для подальших обрахунків необхідно знайти кут між дотичною до Землі і відрізком АВ.

Задачі для самостійного розвязвування