Рівняння та їх властивості. Розв'язування задач за допомогою рівнянь
Тема. Рівняння та їх властивості. Розв'язування задач за допомогою рівнянь
Мета: діагностика рівня засвоєння знань та вмінь, передбачених програмою з названої теми.
Тип уроку: перевірка і корекція знань, умінь та навичок.
Хід уроку
I. Організаційний момент
(Перевіряємо готовність до уроку, збираємо робочі зошити на перевірку; оголошуємо умову та вимоги до виконання завдань тематичної контрольної роботи; критерії оцінювання.)
II. Умова тематичної контрольної роботи
Варіант 1
- Розв'яжіть рівняння: а) 14 + 5х = 4х + 3; б) 4,72 - 2,5х = 2х + 2,92.
- Розв'яжіть задачу складанням рівняння:
Різниця двох чисел дорівнює ![]() , а одне з них у 4 рази більше за інше. Знайдіть ці числа.
, а одне з них у 4 рази більше за інше. Знайдіть ці числа.
- При яких значеннях змінної справджується рівність:
a) ![]() ; б) 0,2(5y - 2) = 0,3(2y – 1) – 0,9.
; б) 0,2(5y - 2) = 0,3(2y – 1) – 0,9.
-
Утрьох цистернах 60 т палива. В першій на 15 т більше, ніжу другій,
а у третій — втричі більше, ніж у другій. Скільки тонн палива у другій
цистерні? -
Знайдіть корені-рівнянь: а)
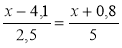 ; б) (-4х - 3)(3х + 0,6)= 0.
; б) (-4х - 3)(3х + 0,6)= 0.
-
Різниця двох чисел дорівнює 5. Знайдіть ці числа, якщо
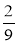 меншого з них дорівнює 20 % від більшого.
меншого з них дорівнює 20 % від більшого.
Варіант 2
- Розв'яжіть рівняння: а) 2х – 16 = -5х - 30; б) 8,5 - 2,15х = 3,05х - 9,5.
- Розв'яжіть задачу складанням рівняння:
Рюкзак важчий від валізи у 2,4 раза. Яка маса валізи, якщо вона менша від маси рюкзака на 9,1 кг?
- При яких значеннях змінної справджується рівність?
а) 2![]() у - 1,27 =
у - 1,27 = ![]() у - 4,77; б) 0,4(х – 9) = 0,7 + 0,3(х + 2).
у - 4,77; б) 0,4(х – 9) = 0,7 + 0,3(х + 2).
-
У трьох цехах заводу 270 верстатів. У першому втричі більше, ніж
у третьому, а в другому — на 20 верстатів більше, ніж у третьому.
Скільки верстатів у третьому цеху? -
Відшукайте корінь рівняння: а)
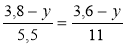 ; б)(5у + 7)(2у – 0,4) = 0.
; б)(5у + 7)(2у – 0,4) = 0.
-
Сума двох чисел дорівнює 138. Знайдіть ці числа, якщо
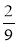 одного з них
одного з них
дорівнює 80 % другого.
III. Розв'язання і відповіді
Варіант 1
-
а) х = -11; б) х =
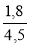 ; х = 0,4.
; х = 0,4.
-
 та
та  .
.
- а) 1,2. б) -2.
- 9т.
-
а) 9. б) -
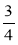 ; -0,2.
; -0,2.
-
Нехай менше число х, тоді більше число х+6.
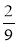 меншого числа — це
меншого числа — це 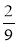 х, 20 % більшого — це 0,2(х+6). За умовою задачі
х, 20 % більшого — це 0,2(х+6). За умовою задачі 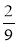 меншого і 20 % більшого числа рівні. Складемо рівняння:
меншого і 20 % більшого числа рівні. Складемо рівняння:
![]() х = 0,2(х + 6); -х =
х = 0,2(х + 6); -х = ![]() (х + 6) | ·45; 10х = 9(х + 6); 10х = 9х + 54; х = 54.
(х + 6) | ·45; 10х = 9(х + 6); 10х = 9х + 54; х = 54.
Отже, менше число 54, а більше 54 + 6 = 60.
Відповідь. 54; 60.
Варіант 2
-
а) х = -2. б) х =
 ; х = 3
; х = 3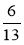 .
.
- 15,6 кг.
- а) -2. б) 49.
- 50 верстатів.
- а) 4. б) -1,4; 0,2.
-
Нехай менше число х, тоді більше число (138 - х). Оскільки
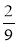 < 0,8, то
< 0,8, то 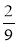 більшого числа, тобто
більшого числа, тобто 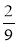 (138 - х)дорівнює за умовою 80 % = 0,8 меншого, або 0,8х. Складемо рівняння:
(138 - х)дорівнює за умовою 80 % = 0,8 меншого, або 0,8х. Складемо рівняння:
0,8х = ![]() (138 - х);
(138 - х); ![]() х =
х = ![]() (138 – х) | ·45; 36х = 10(138 - х);
(138 – х) | ·45; 36х = 10(138 - х);
36х = 1380 - 10х, 46х = 1380; х = ![]() ; х = 30.
; х = 30.
Отже, менше число 30, а більше 138 – 30 = 108.
Відповідь. 30; 108.

про публікацію авторської розробки
Додати розробку
