Розробка уроків до теми "Нерівності"
Матеріал містить 4 уроки у 9 класі за темою "Нерівності". В розробках уроків показано етапи уроку, форми і методи, які можна застосувати при виконанні вправ,надано вправи для усного виконання та письмового,є вправи на диференційований підхід.
Урок № 2
Тема: Числові нерівності
Мета: дати поняття числової нерівності, вчити порівнювати числа за знаком різниці. Розвивати пам'ять, увагу, логічне мислення, спостережливість, обчислювальні навички. Виховувати активність, самостійність, прагнення до знань, повагу, наполегливість, впевненість, культуру записів і мовлення
Тип уроку: засвоєння нових знань
Обладнання: підручник, таблиці, роздатковий матеріал
Хід уроку
І. Організаційний момент
ІІ. Мета і завдання уроку
ІІІ. Актуалізація опорних знань
-Які існують види чисел?
N- натуральні Z- цілі Q- раціональні І-ірраціональні R -дійсні числа. Навести приклади
-Які дії ми виконуємо з числами? Перелічити
Так, ми ще вміємо порівнювати числа.
Порівняти: З коментуванням біля дошки
12 і 7 2,56 і 2,5 ![]() і
і ![]() -13 і - 6
-13 і - 6 ![]() 9 і – 26 0,4 і
9 і – 26 0,4 і ![]()
-Які знаки ми застосували, щоб порівняти числа?
![]()
-Як же називаються вирази, які ми одержали?
Нерівності, а останній вираз називається - рівність.
Ми розпочинаємо вивчати тему «Нерівності та їх властивості».
ІV Сприйняття, усвідомлення та осмислення нового матеріалу
Так щож таке нерівність? Два вирази, сполучені знаком нерівності, утворюють нерівність.
Утворені нами нерівності наз.числовими нерівностями. Хто може пояснити чому вони так називаються?
Запишіть тему уроку «Числові нерівності»
Порівнювати числа люди вміли багато тисячоліть тому. Знаки ![]()
Запишему нерівність 12![]()
12- права частина 7- ліва частина . Запишемо різницю між лівою частиною і правою частинами
12 -7 = 5 , 5![]()
Запишему нерівність -13 ![]()
-13 – ( - 6) = -13 + 6 = - 7 -7 ![]()
![]()
Запишему нерівність 0,4 = ![]() Запишемо різницю між лівою і правою частинами
Запишемо різницю між лівою і правою частинами
0,4 - ![]() різниця = 0
різниця = 0
Ми одержали три випадки знака різниці між лівою і правою частинами нерівності. Зробимо висновок.
a ![]()
![]()
a![]()
![]()
a = b, то a – b = 0
Таким чином можна порівнювати числа за допомогою знака різниці між ними.
V. Закріплення
№1 стор.9 усно
через знак різниці № 16 ![]() - 2 -
- 2 - ![]() =
= ![]() =
= ![]() =
= ![]() = 0
= 0
![]() – 2 =
– 2 = ![]()
2) з коментуванням біля дошки
Порівнювати можна числа виражені змінними. №4 усно
Робота в парі: хто швидше.
Порівняти числа p і c , якщо
p – c = 7 p - c = 19 - ![]()
p - c = - 0,6 p – c = ![]() - 18
- 18
p - c = ![]() p – c =
p – c = ![]()
p - c = -18 + 12 p – c = - 43 + 43
№6 Самостійно . 2 учні за дошкою 1і2 3 і 4 Взаємоперевірка
Пригадаємо, як ще можна порівнювати числа? За допомогою координатної прямої.
![]()
![]()
![]()
![]()
![]()
![]()
p m d 0 c
Записати нерівності.
Що можна сказати про число більше 0 с![]()
Що можна сказати про число менше 0 р![]()
Завдання: Розмістити числа n, t, b, k на координатній прямій, якщо
n![]()
![]()
![]()
Вправа: Незакінчене речення
n![]()
h ![]()
k = p , то k – p …
VІ Рефлексія VІІ Домашнє завдання: Опрацювати §1( зак. мал..1). №2, №5, №7, №8, №17
Урок № 3
Тема: Числові нерівності( продовження)
Мета: закріплювати вміння та навички учнів порівнювати числа за знаком різниці, встановити види знаків числових нерівностей, види нерівностей, вчити доводити нерівності. Розвивати пам'ять, увагу, логічне мислення, спостережливість, обчислювальні навички. Виховувати активність, самостійність, прагнення до знань, повагу, наполегливість, впевненість, культуру записів і мовлення
Тип уроку: комбінований
Обладнання: підручник, таблиці, роздатковий матеріал
Хід уроку
І. Організаційний момент
ІІ. Мета і завдання уроку
ІІІ. Перевірка дз
№2 1) ![]()
![]()
![]()
![]()
![]()
![]()
№5 1) m![]()
![]()
![]()
№7 1) a – 7 = b a – b = 7 a![]()
![]()
![]()
![]() №8
№8
№ 17 1) ![]() - 1 -
- 1 - ![]() =
= ![]() =
= ![]()
![]() - 1
- 1![]()
2) 4 + ![]() -
- ![]() =
= ![]() = 0 4 +
= 0 4 + ![]()
Теоретичне опитування
- Що таке нерівність?
- За допомогою яких знаків ми порівнюємо?
- Як порівняти два числа, знаючи знак їхньої різниці?
- Самостійна робота на аркушах, які здаються на перевірку
|
Самостійна робота№1 І варіант |
Самостійна робота№1 ІІ варіант |
|
1.Порівняти числа:
1,15 і 1
|
1.Порівняти числа:
1,45 і 1 |
|
2. Порівняти змінні:
a) t – c = 13,6 д) а – b = ‒
б) m – n = ‒ 0,03 е) с – k =
в) х – у = ‒
г) р – с =
|
2. Порівняти змінні:
a) m – n = ‒ 8,2 д) р – х = ‒
б) с – к = 0,002 е) а – b =
в) t – n = ‒
г) х – у =
|
|
3.Записати у вигляді нерівності:
а) – 12 ‒ від’ємне число б) 7 – додатне число в) х ‒ від’ємне число г) у ‒ додатне число
|
3.Записати у вигляді нерівності:
а) 9 – додатне число б) – 13‒ від’ємне число в) у ‒ додатне число г) t - від’ємне число
|
ІV Актуалізація опорних знань
Що це за вираз ![]() ? Після розкриття дужок одержимо 16
? Після розкриття дужок одержимо 16 ![]() + 56х + 49
+ 56х + 49
25 ![]() - 30х + 9 =
- 30х + 9 = ![]()
( у – 6 ) ( у + 6 ) = ![]() – 36
– 36
![]() - 81 = ( с – 9 ) ( с + 9 )
- 81 = ( с – 9 ) ( с + 9 )
V Сприйняття, усвідомлення та осмислення нового матеріалу
Ми з вами при порівнянні чисел застосовували знаки ![]()
Наряду з цими знаками застосовують знаки ![]()
![]()
Ці знаки наз. знаками нестрогої нерівності, а нерівності, записані за їх допомогою наз. нестрогими нерівностями.
15 ![]()
![]()
14 ![]()
![]()
Прочитати: 15 ![]()
![]()
![]()
Завдання: Записати у вигляді нерівності 1) х більше або дорівнює 7; 2) с не більше 8; 3) р не менше 12 ;
4) к менше або дорівнює 5
Розглянемо нерівності:
10 ![]()
![]()
![]()
42![]()
![]()
![]()
- 8 ![]()
![]()
![]()
![]()
Що можна про них сказати? Серед них є правильні і є неправильні.
Завдання: Випишіть окремо правильні і окремо неправильні.
Нерівності бувають строгі і нестрогі, правильні і неправильні.
Закріплення № 3 усно.
№ 11 з коментуванням 2, 4, 5 - правильні
Розглянемо, як за допомогою означення порівняння чисел можна доводити нерівності. Про що воно говорить?
№ 12 1) 3m +5 ![]()
3m + 5 – 3 ( m – 1 ) = 3m + 5 – 3m + 3 = 8 ![]()
Далі учні коментують біля дошки.
№ 14 1) біля дошки з коментуванням.
2), 3), 4) самостійно в парах. Захистити біля дошки
VІ Рефлексія VІІ Домашнє завдання: Опрацювати §1 до кінця.№10( перетворити дріб ![]() , №13, №15
, №13, №15
Урок № 4
Тема: Основні властивості числових нерівностей
Мета: закріплювати вміння та навички учнів порівнювати числа за знаком різниці, доводити нерівності. Вчити застосовувати властивості нерівностей при розв’язуванні вправ. Розвивати пам'ять, увагу, логічне мислення, спостережливість, обчислювальні навички. Виховувати активність, самостійність, прагнення до знань, повагу, наполегливість, впевненість, культуру записів і мовлення
Тип уроку: комбінований
Обладнання: підручник, таблиці, роздатковий матеріал
Хід уроку
І. Організаційний момент
ІІ. Мета і завдання уроку
ІІІ. Перевірка дз
№10 -1,2 ![]() 0 - 0,99 0,8 - 0,6 0,51
0 - 0,99 0,8 - 0,6 0,51
-1,2 ![]()
0,8 0,75 0,51 0 - 0,6 -0,99 - 1,2
0,8 ![]() 0,51 0 - 0,6 -0,99 - 1,2
0,51 0 - 0,6 -0,99 - 1,2
№13 1) 2a – 3 ![]()
![]()
2) с( с + 2) ![]()
![]() + 2с – 3
+ 2с – 3 ![]() + 2с – (
+ 2с – (![]() + 2с – 3) =
+ 2с – 3) = ![]() + 2с –
+ 2с – ![]() - 2с +3 = 3
- 2с +3 = 3![]()
3) (х +2 )( х – 2 ) +5 ![]()
![]() - 4 + 5 -
- 4 + 5 - ![]() = 1
= 1![]()
4) 3m – 2 ![]() 3m – 2 – m( m +3 ) = 3m – 2 –
3m – 2 – m( m +3 ) = 3m – 2 – ![]() - 3m = - 2 -
- 3m = - 2 - ![]()
![]()
№15 1) ![]()
![]()
![]()
![]()
![]()
![]()
2) t( t + 2 ) ![]()
![]() + 2t + 1 =
+ 2t + 1 = ![]()
![]()
3) c( c – d ) ![]()
![]() - cd + cd =
- cd + cd = ![]()
![]()
4) ![]() - 11p + 36
- 11p + 36 ![]()
![]() - 11p + 36 – p =
- 11p + 36 – p = ![]() - 12p + 36 =
- 12p + 36 = ![]()
![]()
ІV Аналіз самостійної роботи
Математичний диктант
- У якому випадку число с менше числа р ( число t більше числа m)
- Відомо, що n – d = 7 ( z – c = - 9) Порівняти змінні
-
Правильна чи неправильна нерівність
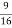
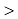
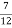 (
( 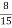
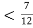 )
)
- Записати нерівністю : число f не більше 16 ( число р більше або дорівнює 8)
Число n більше або дорівнює 11 ( число к не менше 23)
- Порівняти числа с і р, якщо 2с – 18 = 2р – 24 ( 3р – 18 = 3с – 12). ( творче завдання)
Відповіді можна записати в презентації. Взаємоперевірка
ІV Актуалізація опорних знань
1.Порівняти з 0 вирази: ![]() + 9
+ 9 ![]()
![]() - 11
- 11![]()
2.Виділити квадрат двочлена з виразу ![]() - 8х + 6 =
- 8х + 6 = ![]() – 2 ∙ 4 ∙ х + 16 - 16 + 6 =
– 2 ∙ 4 ∙ х + 16 - 16 + 6 = ![]() - 10
- 10
№18 з коментуванням біля дошки 1) ![]() + 10a + 26
+ 10a + 26 ![]()
![]() + 2 ∙5 ∙ a+ 25 - 25 + 26 =
+ 2 ∙5 ∙ a+ 25 - 25 + 26 = ![]() +1
+1![]()
2) Самостійно в парах 8a ![]() + 20 8a
+ 20 8a ![]() - 20 = -
- 20 = - ![]() + 8a – 20= - (
+ 8a – 20= - ( ![]() - 8a +20 )= - (
- 8a +20 )= - ( ![]() - 2 ∙ 4 ∙a +16 - 16+20)=
- 2 ∙ 4 ∙a +16 - 16+20)=
=⎯ ![]() + 4) = =⎯
+ 4) = =⎯ ![]() – 4
– 4 ![]()
Як ще можна працювати з нерівностями? А для цього ми вивчимо властивості числових нерівностей
![]()
![]() V Сприйняття, усвідомлення та осмислення нового матеріалу
V Сприйняття, усвідомлення та осмислення нового матеріалу
![]()
![]()
![]() Розглянемо правильну нерівність 12
Розглянемо правильну нерівність 12 ![]()
![]()
![]() - 6
- 6 ![]()
![]()
Таким чином маємо першу властивість
І Якщо a ![]()
![]()
a ![]()
![]()
![]()
![]()
![]()
![]()
Розглянемо правильні нерівності 9 ![]()
![]()
![]()
![]()
![]()
![]()
![]() Самостійно за зобр. на мал 4
Самостійно за зобр. на мал 4 ![]()
![]()
![]()
Маємо другу властивість 4 7 12
ІІ Якщо a ![]()
![]()
![]()
Якщо a ![]()
![]()
![]()
№ 41 усно 1) х ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
х 5 у у 2 х
Розглянемо нерівність 14 ![]()
14 + 9 ![]()
23 ![]()
Тепер додамо - 4 14 + ( - 4 ) ![]()
10 ![]()
Маємо третю властивість
ІІІ Якщо a ![]()
![]()
Властивість справджується і для нерівності із знаком ![]()
Розглянемо нерівність - 7 ![]()
- 7 ∙ 4 ![]()
![]()
Помножимо обидві частини на (- 3)
- 7 ∙ ( - 3 ) ![]()
![]()
Маємо четверту властивість
ІV Якщо a ![]()
![]()
![]()
Якщо a ![]()
![]()
![]()
Властивість справджується і для нерівності із знаком ![]()
Наслідок: 8![]()
![]()
![]()
![]() Знак змінився
Знак змінився
Якщо a ![]()
![]()
![]()
![]()
Закріплення № 39 з коментуванням
Самостійно: в презентації по варіантах
|
- 15 |
- 24 |
|
+ 7 |
- 7 |
|
: ( - 3 ) |
∙ ( - 4) |
|
- 6 |
+ 2 |
|
∙ 5 |
: ( - 4) |
Взаємоперевірка. Відповіді в презентації
V Рефлексія VІ Домашнє завдання: Опрацювати §2( доведення властивостей у загальному вигляді розібрати самостійно) Вивчити властивості №20, № 40, № 43
Урок № 5
Тема: Розв’язування вправ
Мета: закріплювати вміння та навички учнів застосовувати властивості числових нерівностей при розв’язуванні вправ. Розвивати пам'ять, увагу, логічне мислення, спостережливість, обчислювальні навички. Виховувати активність, самостійність, прагнення до знань, повагу, наполегливість, впевненість, культуру записів і мовлення
Тип уроку: застосування набутих знань
Обладнання: підручник, таблиці, роздатковий матеріал
Хід уроку
І. Організаційний момент
ІІ. Мета і завдання уроку
ІІІ. Перевірка дз
№ 20 1) ![]()
![]()
![]()
№ 40 1) 7 ![]()
![]()
![]()
![]()
![]()
2) 0 ![]()
![]()
![]()
![]()
![]()
№ 43 m ![]()
![]()
![]()
![]() 1) p
1) p ![]()
![]()
![]()
Теоретичне опитування
1.Як порівняти два числа?
2. Які види нерівностей існують?
2. Як довести нерівність?
3. Які властивості числових нерівностей ми знаємо? Пояснити на прикладі
Маємо нерівність 24 ![]()
+ 5 29 ![]()
![]()
- 8 16 ![]()
![]()
∙ 3 72 ![]()
![]()
Оберн ![]()
![]()
![]()
У яких випадках знак нерівності змінюється?
Робота по рівнях.Біля дошки 4 учні Всі останні учні обирають собі рівень самостійно
|
І рівень |
ІІ рівень |
ІІІ рівень |
ІV рівень |
|
18 |
- 32 |
- 42 |
- 48 |
Роботу перевірити
ІV Актуалізація опорних знань
Маємо нерівність: х ![]()
Порівняти вирази : х – 9 ![]()
![]()
![]() - 2
- 2 ![]()
![]() - 2
- 2
- 7х ![]()
![]()
![]()
![]()
![]()
![]()
![]()
х + 3 ![]()
![]()
![]()
![]()
![]()
Самостійно в парах № 46. Захист біля дошки
V Сприйняття, усвідомлення та осмислення застосування властивостей нерівностей
Продовжуємо вивчати відомості про нерівності. Пригадаємо, як називається така нерівність
12 ![]()
![]()
Прочитати: - 6 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Назвіть всі цілі значення для х , які будуть задовольняти нерівність?
Подвійні нерівності використовують для оцінювання значення виразів.
Завдання: Відомо, що 8 ![]()
![]()
Оцінити значення виразів: з коментуванням біля дошки. Три учні по черзі
-
8+ 7
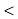
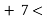
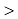
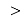
15 ![]()
![]()
![]()
![]()
- 90 ![]()
![]()
2 8 ![]()
![]()
24![]()
![]()
Самостійно № 48. 2 учні працюють за дошкою
Тестове завдання:
a – сторона рівностороннього трикутника і 6![]()
А. 12 ![]()
![]()
![]()
![]()
Б. 24 ![]()
![]()
![]()
![]()
№ 50 №53 усно
V Рефлексія VІ Домашнє завдання: Опрацювати §2( до кінця) Повт.властивості № 45, № 47, № 49


про публікацію авторської розробки
Додати розробку
