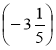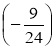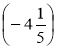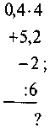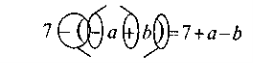Розробка уроку на тему "Розкриття дужок."

Тема. Розкриття дужок.

Мета: основуючись на відомих учням властивостях додавання раціо­нальних чисел, сформулювати правила розкриття дужок та виробити вміння застосовувати ці правила для розв'язування вправ на обчислення та спрощення виразів.

Тип уроку: засвоєння нових знань, умінь і навичок.

Хід уроку

І. Перевірка домашнього завдання

1. Збираємо зошити на перевірку після виконання самостійної роботи.
2. Самостійна робота.

II. Актуалізація опорних знань

Усні вправи

2. Серед виразів знайдіть рівні:

a) a + (b + c); б) а - (b + с);  в) (а + b) - с; г) a - b - c;   д) а + b - с;

е) a - c + b;    ж) а + b + с;   з) а + с - b;    к) а; л) +а;   м) -(-а).

3. Прочитайте записи, використовуючи слова «число, протилежне до...»:

а) -(-5); б) -3,2; в) 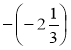; г) -а; д) -(а + 1); е) -(-а).

Як спростити ці записи?

4. Замініть віднімання додаванням у виразах:

а) 4 – 6; б) 4 – (-6); в) а - b; г) а - (b + с); д) а - (-b + с).

5. Обчисліть найзручнішим способом:

-3 + (3 + (-5)); -12 + (-14 + 28).

III. Формування знань

 Ця тема є дуже важливою для успішного вивчення математики в наступних класах. Тому треба, вже починаючи з цього уроку, ви­магати від учнів розуміння і точного засвоєння та відтворення правил розкриття дужок; не менш важливим є і відпрацювання навичок застосування цих правил для спрощення виразів. Для кращого розуміння (а отже, і запам'ятовування) правил пропо­нуємо трохи відступити від тексту викладення матеріалу, який традиційно подано в підручниках, а саме: спочатку знову ж таки на конкретних прикладах показати виконання цих правил (не за­буваймо — шестикласники поки що в основному мають конкрет­не, а не розвинене логічне мислення), а потім вже формулювати відповідні загальні правила.

Мотивація навчальної діяльності

Вправи № 2—5 (див. усні вправи) нам показують, що, по-перше, є такі властивості, які допомагають змінювати порядок виконання дій у виразах, а також, по-друге, замінювати одні дії іншими.

Сьогодні на уроці ми дізнаємось про ще один спосіб «перетворення» виразів, а саме: «розкриття дужок».

Розкриття дужок, перед якими стоїть знак «+»

Завдання 1. Обчисліть значення виразів і порівняйте результати.

а) 11 + (45 – 17); б) (11 + 45) + (-17); в) 11 + 45 - 17;

г) 11+ (-17 + 45); д) 11-17 + 45; є) (11 + (-17)) + 45.

Розв'язання. Зрозуміло, що після виконання дій у всіх виразах дістане­мо однакове значення виразів, а саме: 39. Порівнявши самі вирази, бачи­мо, що вони відрізняються лише наявністю або відсутністю дужок, тому можна записати 11 + (45 – 17) = 11 + 45 – 17, бачимо, що цей результат можна було дістати, розкривши дужки, а тому робимо висновок 1.

Щоб розкрити дужки, перед якими стоїть знак «+», треба: 1) опусти­ти дужки і знак «+», що стоять перед ними; 2) записати всі доданки зі своїми знаками:              a + (b + c) = a+b+c.

Наприклад,

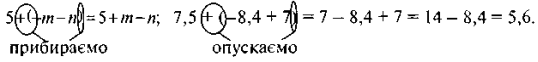
Завдання 2. Обчисліть значення виразів та порівняйте результат:

а) -6 + 4; б) - (-6 + 4); в) 6 + (-4).

Розв'язання. Очевидно, що маємо в п. а) -2, а в п. б), в) 2. Можемо записати це так: -(-6 + 4) = 6 + (-4) — це число, протилежне до зна­чення виразу (-6 ї 4).

Порівнявши записи, помітимо, що вираз, протилежний до суми, є також сума, але доданки є протилежними до даних.

Висновок 2. Вираз, протилежний до суми, є сума протилежних до­данків.

Наприклад

а) –(3 – 4) = - (3 + (-4)) = -3 + 4 = 1;

б) –(a + b)= -a + (-b) = -a – b;

в) - (a – b + c) = - a + (b) + (-c) = - a + b – c.

Правило розкриття дужок, перед якими стоїть знак «-»

Завдання 3. Використовуючи правило віднімання, розкрийте дужки у виразі 5 - (3 + 7).

Розв'язання.

5 – (3 + 7) = 5 + ( - (3 + 7)) = 5 + (- 3 - 7) = 5 - 3 - 7 = -5 або, замінивши числа на букви, маємо:

a - (b + c) = a + (- (b + c)) = a + (-b - c) = a – b – c.

Порівнявши записи, які ми мали з дужками, і записи, які не містять дужок, доходимо висновку, що дужки, перед якими стоїть знак «мінус», розкриваються так.

Висновок 3. Щоб розкрити дужки, перед якими стоїть знак «мінус», треба:

1. опустити дужки і знак «-», що стоїть перед ними;
2. всі доданки, що стояли в дужках, записати із протилежними знаками.

Наприклад

III. Закріплення знань. Засвоєння вмінь

Усні вправи

1. Чи правильно розкрито дужки?

а) 3 + (-5 - 2) = 3 - 5 - 2;   б) 3 - (-5 + 2) = 3 + 5 - 2;

в) 3 - (5 - 2) = 3 - 5 - 2;   г) 3 - (5 + 2) = 3 - 5 + 2.

2. Заповніть пропуски ... відповідними знаками («+» або «-»), щоб роз­криття дужок було виконано правильно:

а) -3 - (m + n) = ... 3 ... m ... n;   

б) 5 + (-a + b - c) = ... 5 ... a... b. . с;

в) 7 - (-k + р + t) = ... 7... k ... p ... t; 

г) m + 3 - (т – п + 4) = ... т ... 3 ... т ... п ... 4;

д) m + 3 - (m – n) + 4 = ... т ... 3 ... т ... n ... 4.

   Типова помилка учнів під час розкриття дужок, перед якими стоїть знак «-»: змінюють знак усіх доданків — і тих, що стоять у дужках, і тих, що стояли поза дужками. Тому, щоб попередити ці помилки, одразу звертаємо увагу на той момент, що під час роз­криття дужок змінюється знак тільки тих доданків, що стоять у дужках.

Письмові вправи

I рівень

1. Обчисліть:

а) - 6 + 9 + 6;  б) - 7 + 9 + (- 2);   в) - 5 + 31 + 5 + (- 31);

г) - 27 + 5 + (- 4) + 27;  д) - 7 + 11 + 8 - 12;  є) 3 + 7 + (- 3) + (- 1).

2. Розкрийте дужки:

а) 5 + (m - n); б) 7 - (-а + b);  в)-3 - (m + n); г) 5 - (а – b + с).

3. Розкрийте дужки і спростіть вираз:

а) 0,9 - (а + 3,7);   б) - (4 – а + 0,2) - 11,8;

в) b + (7,8 – b – 1,9),  г) - (а + 5,1) - (-а - 4,9).

II рівень (якщо встигнемо)

4. Спростіть вираз  a + b – (b – c) + d і знайдіть його значення,

якщо a = -3,1; b = 0,017, с = -0,2; d = -5.

V. Підсумок уроку

Запитання до класу

1. Як розкрити дужки, перед якими стоїть знак «+»?
2. Як розкрити дужки, перед якими стоїть знак «-»?

VI. Домашнє завдання

1. Розкрийте дужки і знайдіть значення виразу:

а) - 32 - (53 - 72); б) 40 - (- 17 + 35); в) - 12 + (- 32 - 17);

г) - 3,8 -(-8,1+ 3,9); д) 7,5 + (- 8,4 + 7); є) .

2. Спростіть вираз:

а) -0,24 - (5,6 - а);  б) 4,1 - (5,2 + b - 1,5);

в) - (-5 + а) - 7,2;  г) - (а – 6) + (4,2 + а – 5,8).

Вправи на повторення

1. Периметр трикутника ABC дорівнює 15 см. Довжина сторони АВ становить 44 % периметра, а довжина сторони ВС становить 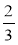довжини сторони АВ. Яка довжина сторони АС?
2. Розв'яжіть рівняння: а) 5 + х = -7,8; б) 4 – х = -1,2.